在我看来,第一步是计算每一列所需的最小高度。以您的图片为例,第一列至少需要高度为10,这是由红色、绿色和小蓝色矩形贡献的。这可以通过迭代每个给定的矩形并将其对应的高度添加到它所占据的列中来轻松完成。通过这样做,找到所有“列高度”中的最大值,我称之为“柱子”。在您的图片中,“柱子”位于列8:10,高度为14,由矩形1、2、4、6(从下往上编号)贡献。这意味着包装的最小高度至少是“柱子”的高度,因为“柱子”列是实心填充的,不能进一步减少。将这四个矩形堆叠起来形成这样的图片:(未显示非“柱子”矩形)
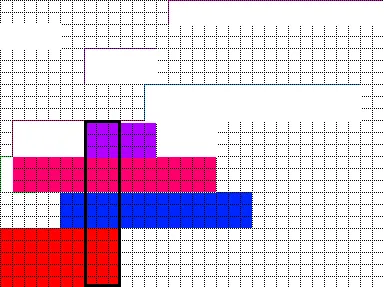
然后,柱子将图片分为两部分,一部分在柱子左侧,另一部分在另一侧。此外,“非柱子”矩形(R3、5、7、8)也分别放置在两个区域中。R3、R7在LHS上,R5、R8在RHS上。
现在先考虑左侧部分。我按照如图所示重新排列了柱子的矩形(fig.3):
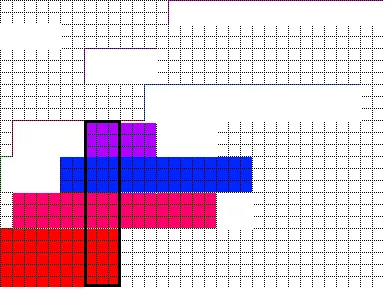
通过重新排列的柱子矩形堆叠顺序,虽然我没有严格的证明,但很可能无论什么形状和数量的矩形都可以放置在柱子左侧的空白区域中(这里的约束是这些矩形不能给出更高的实心柱子,否则步骤1会检测到并将其用作实际柱子)。此安排使得左侧的空白区域具有最佳的“空间一致性”,这意味着每个柱子矩形创建的空白空间从下往上按升序堆叠。这种“一致性”让每个柱子矩形创建的空白空间“共同工作”,然后包含比任何单个柱子矩形创建的单个空白空间更高的矩形。例如,下一个图片中的绿色矩形是使用蓝色和紫色矩形一起创建的空白空间来适应的。
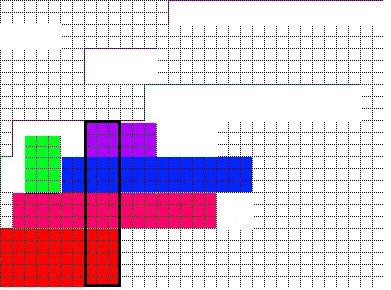
假设上面的陈述是正确的,那么左边的矩形永远不会比支柱高。但是,如果这些矩形需要在左侧之间进行任何合作才能适应,则它们实际上限制了支柱矩形的交换可能性。以图3为例,绿色矩形需要紫色和蓝色相邻才能适应,然而,为了在RHS上获得最佳空间一致性,洋红色必须放在紫色和蓝色之间。这意味着LHS上的绿色使得在RHS上定位的矩形无法适应空白区域,并且超过了支柱设置的高度,从而可能导致堆叠出现孔和超过支柱高度。很抱歉我不能在这里设计这样的情况,但它确实有所不同。
总之:
第一步是找到支柱,如果每个给定的矩形都涉及支柱,则可以在此处找到一个简单的答案-支柱的高度是最小堆叠高度。
第二步是检查支柱两侧。
情况a:如果一侧没有自由矩形定位,则另一侧可以轻松地使用“最佳一致性”方法填充,从而导致最小堆叠高度再次为支柱高度。
情况b:如果一侧不需要自由空间一致性,则该侧可以填充,而另一侧仍然可以使用“最佳一致性”。例如:(您的原始图片)
在这种情况下,适合R3所需的空白空间仅由R6创建,适用于R7和R2。因此,将R6和R2的堆叠顺序与其他支柱矩形交换不会使R3,R7不适合于R3,R7遵循交换。这可以导致RHS的“最佳一致性”情况:
然后,RHS可以用RHS定位的矩形填充,而不超过支柱高度。
可以通过比较要适应的自由矩形的高度和要为其创建自由空间的支柱矩形的高度来识别不需要一致性的情况。如果自由矩形的高度不大于另一个矩形,则不需要第二个支柱矩形参与其中,这意味着它不需要自由空间的一致性。
情况c: 双方需要自由空间的一致性。这就是问题出现的地方。再以图3为例。图3中的绿色与紫色和蓝色相结合。这意味着绿色、紫色和蓝色被视为一个整体,以与其他柱形矩形交换堆叠顺序,以便得到LHS的自由矩形最佳适配。在这个整体中,蓝色和紫色也可以交换。
如果RHS无法适配,则需要重复步骤二,但先适配RHS,然后尝试适配LHS。然后将比较后的较低装载高度结果作为最终结果。对于这种情况的逻辑不清楚,极有可能有更好的替代方案。
我知道这不能算作一个合适的解决方案,而只是随意的思考,但显然它无法适应评论区。请原谅我拙劣的解释和图片处理能力。希望这可以帮到您。
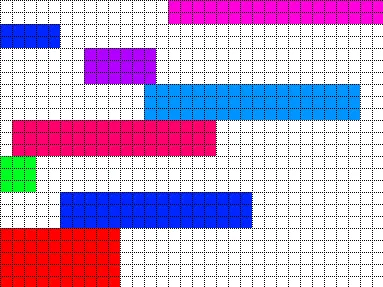 使总高度尽可能低,但是必须满足矩形必须最终停留在它们开始的同一列中。 矩形允许“穿过”彼此以达到最终状态,只要它们在结束时不相交。
使总高度尽可能低,但是必须满足矩形必须最终停留在它们开始的同一列中。 矩形允许“穿过”彼此以达到最终状态,只要它们在结束时不相交。 使总高度尽可能低,但是必须满足矩形必须最终停留在它们开始的同一列中。 矩形允许“穿过”彼此以达到最终状态,只要它们在结束时不相交。
使总高度尽可能低,但是必须满足矩形必须最终停留在它们开始的同一列中。 矩形允许“穿过”彼此以达到最终状态,只要它们在结束时不相交。

