double和BigDecimal数据类型访问。但在计算Zeta函数的大数值时会出现重大问题。Zeta函数的数值近似参考: 直接在高值处评估这个近似会出现问题,例如当
s = (230+30i)时,其具有大的复杂形式。我非常感谢在这里获得关于此的信息here。由于我在adaptiveQuad方法中写错了一些内容,所以S2.minus(S1)的评估会产生错误。例如,通过这个程序计算
Zeta(2+3i)可以生成:Calculation of the Riemann Zeta Function in the form Zeta(s) = a + ib.
Enter the value of [a] inside the Riemann Zeta Function: 2
Enter the value of [b] inside the Riemann Zeta Function: 3
The value for Zeta(s) is 7.980219851133409E-1 - 1.137443081631288E-1*i
Total time taken is 0.469 seconds.
哪一个是 正确。
Zeta(100+0i) 生成
Calculation of the Riemann Zeta Function in the form Zeta(s) = a + ib.
Enter the value of [a] inside the Riemann Zeta Function: 100
Enter the value of [b] inside the Riemann Zeta Function: 0
The value for Zeta(s) is 1.000000000153236E0
Total time taken is 0.672 seconds.
相对于Wolfram,这也是正确的。问题出在被标记为
adaptiveQuad的方法内部。
Zeta(230+30i)生成。Calculation of the Riemann Zeta Function in the form Zeta(s) = a + ib.
Enter the value of [a] inside the Riemann Zeta Function: 230
Enter the value of [b] inside the Riemann Zeta Function: 30
The value for Zeta(s) is 0.999999999999093108519845391615339162047254997503854254342793916541606842461539820124897870147977114468145672577664412128509813042591501204781683860384769321084473925620572315416715721728082468412672467499199310913504362891199180150973087384370909918493750428733837552915328069343498987460727711606978118652477860450744628906250 - 38.005428584222228490409289204403133867487950535704812764806874887805043029499897666636162309572126423385487374863788363786029170239477119910868455777891701471328505006916099918492113970510619110472506796418206225648616641319533972054228283869713393805956289770456519729094756021581247296126093715429306030273437500E-15*i
Total time taken is 1.746 seconds.
虚部与Wolfram相比略有不同。
评估积分的算法被称为自适应求积法,可在此处找到
double Java实现here。自适应求积法应用以下方法。// adaptive quadrature
public static double adaptive(double a, double b) {
double h = b - a;
double c = (a + b) / 2.0;
double d = (a + c) / 2.0;
double e = (b + c) / 2.0;
double Q1 = h/6 * (f(a) + 4*f(c) + f(b));
double Q2 = h/12 * (f(a) + 4*f(d) + 2*f(c) + 4*f(e) + f(b));
if (Math.abs(Q2 - Q1) <= EPSILON)
return Q2 + (Q2 - Q1) / 15;
else
return adaptive(a, c) + adaptive(c, b);
}
这是我第四次尝试编写该程序
/**************************************************************************
**
** Abel-Plana Formula for the Zeta Function
**
**************************************************************************
** Axion004
** 08/16/2015
**
** This program computes the value for Zeta(z) using a definite integral
** approximation through the Abel-Plana formula. The Abel-Plana formula
** can be shown to approximate the value for Zeta(s) through a definite
** integral. The integral approximation is handled through the Composite
** Simpson's Rule known as Adaptive Quadrature.
**************************************************************************/
import java.util.*;
import java.math.*;
public class AbelMain5 extends Complex {
private static MathContext MC = new MathContext(512,
RoundingMode.HALF_EVEN);
public static void main(String[] args) {
AbelMain();
}
// Main method
public static void AbelMain() {
double re = 0, im = 0;
double start, stop, totalTime;
Scanner scan = new Scanner(System.in);
System.out.println("Calculation of the Riemann Zeta " +
"Function in the form Zeta(s) = a + ib.");
System.out.println();
System.out.print("Enter the value of [a] inside the Riemann Zeta " +
"Function: ");
try {
re = scan.nextDouble();
}
catch (Exception e) {
System.out.println("Please enter a valid number for a.");
}
System.out.print("Enter the value of [b] inside the Riemann Zeta " +
"Function: ");
try {
im = scan.nextDouble();
}
catch (Exception e) {
System.out.println("Please enter a valid number for b.");
}
start = System.currentTimeMillis();
Complex z = new Complex(new BigDecimal(re), new BigDecimal(im));
System.out.println("The value for Zeta(s) is " + AbelPlana(z));
stop = System.currentTimeMillis();
totalTime = (double) (stop-start) / 1000.0;
System.out.println("Total time taken is " + totalTime + " seconds.");
}
/**
* The definite integral for Zeta(z) in the Abel-Plana formula.
* <br> Numerator = Sin(z * arctan(t))
* <br> Denominator = (1 + t^2)^(z/2) * (e^(2*pi*t) - 1)
* @param t - the value of t passed into the integrand.
* @param z - The complex value of z = a + i*b
* @return the value of the complex function.
*/
public static Complex f(double t, Complex z) {
Complex num = (z.multiply(Math.atan(t))).sin();
Complex D1 = new Complex(1 + t*t).pow(z.divide(TWO));
Complex D2 = new Complex(Math.pow(Math.E, 2.0*Math.PI*t) - 1.0);
Complex den = D1.multiply(D2);
return num.divide(den, MC);
}
/**
* Adaptive quadrature - See http://www.mathworks.com/moler/quad.pdf
* @param a - the lower bound of integration.
* @param b - the upper bound of integration.
* @param z - The complex value of z = a + i*b
* @return the approximate numerical value of the integral.
*/
public static Complex adaptiveQuad(double a, double b, Complex z) {
double EPSILON = 1E-10;
double step = b - a;
double c = (a + b) / 2.0;
double d = (a + c) / 2.0;
double e = (b + c) / 2.0;
Complex S1 = (f(a, z).add(f(c, z).multiply(FOUR)).add(f(b, z))).
multiply(step / 6.0);
Complex S2 = (f(a, z).add(f(d, z).multiply(FOUR)).add(f(c, z).multiply
(TWO)).add(f(e, z).multiply(FOUR)).add(f(b, z))).multiply
(step / 12.0);
Complex result = (S2.subtract(S1)).divide(FIFTEEN, MC);
if(S2.subtract(S1).mod() <= EPSILON)
return S2.add(result);
else
return adaptiveQuad(a, c, z).add(adaptiveQuad(c, b, z));
}
/**
* The definite integral for Zeta(z) in the Abel-Plana formula.
* <br> value = 1/2 + 1/(z-1) + 2 * Integral
* @param z - The complex value of z = a + i*b
* @return the value of Zeta(z) through value and the
* quadrature approximation.
*/
public static Complex AbelPlana(Complex z) {
Complex C1 = ONEHALF.add(ONE.divide(z.subtract(ONE), MC));
Complex C2 = TWO.multiply(adaptiveQuad(1E-16, 100.0, z));
if ( z.real().doubleValue() == 0 && z.imag().doubleValue() == 0)
return new Complex(0.0, 0.0);
else
return C1.add(C2);
}
}
复数(BigDecimal)
/**************************************************************************
**
** Complex Numbers
**
**************************************************************************
** Axion004
** 08/20/2015
**
** This class is necessary as a helper class for the calculation of
** imaginary numbers. The calculation of Zeta(z) inside AbelMain is in
** the form of z = a + i*b.
**************************************************************************/
import java.math.BigDecimal;
import java.math.MathContext;
import java.text.DecimalFormat;
import java.text.NumberFormat;
public class Complex extends Object{
private BigDecimal re;
private BigDecimal im;
/**
BigDecimal constant for zero
*/
final static Complex ZERO = new Complex(BigDecimal.ZERO) ;
/**
BigDecimal constant for one half
*/
final static Complex ONEHALF = new Complex(new BigDecimal(0.5));
/**
BigDecimal constant for one
*/
final static Complex ONE = new Complex(BigDecimal.ONE);
/**
BigDecimal constant for two
*/
final static Complex TWO = new Complex(new BigDecimal(2.0));
/**
BigDecimal constant for four
*/
final static Complex FOUR = new Complex(new BigDecimal(4.0)) ;
/**
BigDecimal constant for fifteen
*/
final static Complex FIFTEEN = new Complex(new BigDecimal(15.0)) ;
/**
Default constructor equivalent to zero
*/
public Complex() {
re = BigDecimal.ZERO;
im = BigDecimal.ZERO;
}
/**
Constructor with real part only
@param x Real part, BigDecimal
*/
public Complex(BigDecimal x) {
re = x;
im = BigDecimal.ZERO;
}
/**
Constructor with real part only
@param x Real part, double
*/
public Complex(double x) {
re = new BigDecimal(x);
im = BigDecimal.ZERO;
}
/**
Constructor with real and imaginary parts in double format.
@param x Real part
@param y Imaginary part
*/
public Complex(double x, double y) {
re= new BigDecimal(x);
im= new BigDecimal(y);
}
/**
Constructor for the complex number z = a + i*b
@param re Real part
@param im Imaginary part
*/
public Complex (BigDecimal re, BigDecimal im) {
this.re = re;
this.im = im;
}
/**
Real part of the Complex number
@return Re[z] where z = a + i*b.
*/
public BigDecimal real() {
return re;
}
/**
Imaginary part of the Complex number
@return Im[z] where z = a + i*b.
*/
public BigDecimal imag() {
return im;
}
/**
Complex conjugate of the Complex number
in which the conjugate of z is z-bar.
@return z-bar where z = a + i*b and z-bar = a - i*b
*/
public Complex conjugate() {
return new Complex(re, im.negate());
}
/**
* Returns the sum of this and the parameter.
@param augend the number to add
@param mc the context to use
@return this + augend
*/
public Complex add(Complex augend,MathContext mc)
{
//(a+bi)+(c+di) = (a + c) + (b + d)i
return new Complex(
re.add(augend.re,mc),
im.add(augend.im,mc));
}
/**
Equivalent to add(augend, MathContext.UNLIMITED)
@param augend the number to add
@return this + augend
*/
public Complex add(Complex augend)
{
return add(augend, MathContext.UNLIMITED);
}
/**
Addition of Complex number and a double.
@param d is the number to add.
@return z+d where z = a+i*b and d = double
*/
public Complex add(double d){
BigDecimal augend = new BigDecimal(d);
return new Complex(this.re.add(augend, MathContext.UNLIMITED),
this.im);
}
/**
* Returns the difference of this and the parameter.
@param subtrahend the number to subtract
@param mc the context to use
@return this - subtrahend
*/
public Complex subtract(Complex subtrahend, MathContext mc)
{
//(a+bi)-(c+di) = (a - c) + (b - d)i
return new Complex(
re.subtract(subtrahend.re,mc),
im.subtract(subtrahend.im,mc));
}
/**
* Equivalent to subtract(subtrahend, MathContext.UNLIMITED)
@param subtrahend the number to subtract
@return this - subtrahend
*/
public Complex subtract(Complex subtrahend)
{
return subtract(subtrahend,MathContext.UNLIMITED);
}
/**
Subtraction of Complex number and a double.
@param d is the number to subtract.
@return z-d where z = a+i*b and d = double
*/
public Complex subtract(double d){
BigDecimal subtrahend = new BigDecimal(d);
return new Complex(this.re.subtract(subtrahend, MathContext.UNLIMITED),
this.im);
}
/**
* Returns the product of this and the parameter.
@param multiplicand the number to multiply by
@param mc the context to use
@return this * multiplicand
*/
public Complex multiply(Complex multiplicand, MathContext mc)
{
//(a+bi)(c+di) = (ac - bd) + (ad + bc)i
return new Complex(
re.multiply(multiplicand.re,mc).subtract(im.multiply
(multiplicand.im,mc),mc),
re.multiply(multiplicand.im,mc).add(im.multiply
(multiplicand.re,mc),mc));
}
/**
Equivalent to multiply(multiplicand, MathContext.UNLIMITED)
@param multiplicand the number to multiply by
@return this * multiplicand
*/
public Complex multiply(Complex multiplicand)
{
return multiply(multiplicand,MathContext.UNLIMITED);
}
/**
Complex multiplication by a double.
@param d is the double to multiply by.
@return z*d where z = a+i*b and d = double
*/
public Complex multiply(double d){
BigDecimal multiplicand = new BigDecimal(d);
return new Complex(this.re.multiply(multiplicand, MathContext.UNLIMITED)
,this.im.multiply(multiplicand, MathContext.UNLIMITED));
}
/**
Modulus of a Complex number or the distance from the origin in
* the polar coordinate plane.
@return |z| where z = a + i*b.
*/
public double mod() {
if ( re.doubleValue() != 0.0 || im.doubleValue() != 0.0)
return Math.sqrt(re.multiply(re).add(im.multiply(im))
.doubleValue());
else
return 0.0;
}
/**
* Modulus of a Complex number squared
* @param z = a + i*b
* @return |z|^2 where z = a + i*b
*/
public double abs(Complex z) {
double doubleRe = re.doubleValue();
double doubleIm = im.doubleValue();
return doubleRe * doubleRe + doubleIm * doubleIm;
}
public Complex divide(Complex divisor)
{
return divide(divisor,MathContext.UNLIMITED);
}
/**
* The absolute value squared.
* @return The sum of the squares of real and imaginary parts.
* This is the square of Complex.abs() .
*/
public BigDecimal norm()
{
return re.multiply(re).add(im.multiply(im)) ;
}
/**
* The absolute value of a BigDecimal.
* @param mc amount of precision
* @return BigDecimal.abs()
*/
public BigDecimal abs(MathContext mc)
{
return BigDecimalMath.sqrt(norm(),mc) ;
}
/** The inverse of the the Complex number.
@param mc amount of precision
@return 1/this
*/
public Complex inverse(MathContext mc)
{
final BigDecimal hyp = norm() ;
/* 1/(x+iy)= (x-iy)/(x^2+y^2 */
return new Complex( re.divide(hyp,mc), im.divide(hyp,mc)
.negate() ) ;
}
/** Divide through another BigComplex number.
@param oth the other complex number
@param mc amount of precision
@return this/other
*/
public Complex divide(Complex oth, MathContext mc)
{
/* implementation: (x+iy)/(a+ib)= (x+iy)* 1/(a+ib) */
return multiply(oth.inverse(mc),mc) ;
}
/**
Division of Complex number by a double.
@param d is the double to divide
@return new Complex number z/d where z = a+i*b
*/
public Complex divide(double d){
BigDecimal divisor = new BigDecimal(d);
return new Complex(this.re.divide(divisor, MathContext.UNLIMITED),
this.im.divide(divisor, MathContext.UNLIMITED));
}
/**
Exponential of a complex number (z is unchanged).
<br> e^(a+i*b) = e^a * e^(i*b) = e^a * (cos(b) + i*sin(b))
@return exp(z) where z = a+i*b
*/
public Complex exp () {
return new Complex(Math.exp(re.doubleValue()) * Math.cos(im.
doubleValue()), Math.exp(re.doubleValue()) *
Math.sin(im.doubleValue()));
}
/**
The Argument of a Complex number or the angle in radians
with respect to polar coordinates.
<br> Tan(theta) = b / a, theta = Arctan(b / a)
<br> a is the real part on the horizontal axis
<br> b is the imaginary part of the vertical axis
@return arg(z) where z = a+i*b.
*/
public double arg() {
return Math.atan2(im.doubleValue(), re.doubleValue());
}
/**
The log or principal branch of a Complex number (z is unchanged).
<br> Log(a+i*b) = ln|a+i*b| + i*Arg(z) = ln(sqrt(a^2+b^2))
* + i*Arg(z) = ln (mod(z)) + i*Arctan(b/a)
@return log(z) where z = a+i*b
*/
public Complex log() {
return new Complex(Math.log(this.mod()), this.arg());
}
/**
The square root of a Complex number (z is unchanged).
Returns the principal branch of the square root.
<br> z = e^(i*theta) = r*cos(theta) + i*r*sin(theta)
<br> r = sqrt(a^2+b^2)
<br> cos(theta) = a / r, sin(theta) = b / r
<br> By De Moivre's Theorem, sqrt(z) = sqrt(a+i*b) =
* e^(i*theta / 2) = r(cos(theta/2) + i*sin(theta/2))
@return sqrt(z) where z = a+i*b
*/
public Complex sqrt() {
double r = this.mod();
double halfTheta = this.arg() / 2;
return new Complex(Math.sqrt(r) * Math.cos(halfTheta), Math.sqrt(r) *
Math.sin(halfTheta));
}
/**
The real cosh function for Complex numbers.
<br> cosh(theta) = (e^(theta) + e^(-theta)) / 2
@return cosh(theta)
*/
private double cosh(double theta) {
return (Math.exp(theta) + Math.exp(-theta)) / 2;
}
/**
The real sinh function for Complex numbers.
<br> sinh(theta) = (e^(theta) - e^(-theta)) / 2
@return sinh(theta)
*/
private double sinh(double theta) {
return (Math.exp(theta) - Math.exp(-theta)) / 2;
}
/**
The sin function for the Complex number (z is unchanged).
<br> sin(a+i*b) = cosh(b)*sin(a) + i*(sinh(b)*cos(a))
@return sin(z) where z = a+i*b
*/
public Complex sin() {
return new Complex(cosh(im.doubleValue()) * Math.sin(re.doubleValue()),
sinh(im.doubleValue())* Math.cos(re.doubleValue()));
}
/**
The cos function for the Complex number (z is unchanged).
<br> cos(a +i*b) = cosh(b)*cos(a) + i*(-sinh(b)*sin(a))
@return cos(z) where z = a+i*b
*/
public Complex cos() {
return new Complex(cosh(im.doubleValue()) * Math.cos(re.doubleValue()),
-sinh(im.doubleValue()) * Math.sin(re.doubleValue()));
}
/**
The hyperbolic sin of the Complex number (z is unchanged).
<br> sinh(a+i*b) = sinh(a)*cos(b) + i*(cosh(a)*sin(b))
@return sinh(z) where z = a+i*b
*/
public Complex sinh() {
return new Complex(sinh(re.doubleValue()) * Math.cos(im.doubleValue()),
cosh(re.doubleValue()) * Math.sin(im.doubleValue()));
}
/**
The hyperbolic cosine of the Complex number (z is unchanged).
<br> cosh(a+i*b) = cosh(a)*cos(b) + i*(sinh(a)*sin(b))
@return cosh(z) where z = a+i*b
*/
public Complex cosh() {
return new Complex(cosh(re.doubleValue()) *Math.cos(im.doubleValue()),
sinh(re.doubleValue()) * Math.sin(im.doubleValue()));
}
/**
The tan of the Complex number (z is unchanged).
<br> tan (a+i*b) = sin(a+i*b) / cos(a+i*b)
@return tan(z) where z = a+i*b
*/
public Complex tan() {
return (this.sin()).divide(this.cos());
}
/**
The arctan of the Complex number (z is unchanged).
<br> tan^(-1)(a+i*b) = 1/2 i*(log(1-i*(a+b*i))-log(1+i*(a+b*i))) =
<br> -1/2 i*(log(i*a - b+1)-log(-i*a + b+1))
@return arctan(z) where z = a+i*b
*/
public Complex atan(){
Complex ima = new Complex(0.0,-1.0); //multiply by negative i
Complex num = new Complex(this.re.doubleValue(),this.im.doubleValue()
-1.0);
Complex den = new Complex(this.re.negate().doubleValue(),this.im
.negate().doubleValue()-1.0);
Complex two = new Complex(2.0, 0.0); // divide by 2
return ima.multiply(num.divide(den).log()).divide(two);
}
/**
* The Math.pow equivalent of two Complex numbers.
* @param z - the complex base in the form z = a + i*b
* @return z^y where z = a + i*b and y = c + i*d
*/
public Complex pow(Complex z){
Complex a = z.multiply(this.log(), MathContext.UNLIMITED);
return a.exp();
}
/**
* The Math.pow equivalent of a Complex number to the power
* of a double.
* @param d - the double to be taken as the power.
* @return z^d where z = a + i*b and d = double
*/
public Complex pow(double d){
Complex a=(this.log()).multiply(d);
return a.exp();
}
/**
Override the .toString() method to generate complex numbers, the
* string representation is now a literal Complex number.
@return a+i*b, a-i*b, a, or i*b as desired.
*/
public String toString() {
NumberFormat formatter = new DecimalFormat();
formatter = new DecimalFormat("#.###############E0");
if (re.doubleValue() != 0.0 && im.doubleValue() > 0.0) {
return formatter.format(re) + " + " + formatter.format(im)
+"*i";
}
if (re.doubleValue() !=0.0 && im.doubleValue() < 0.0) {
return formatter.format(re) + " - "+ formatter.format(im.negate())
+ "*i";
}
if (im.doubleValue() == 0.0) {
return formatter.format(re);
}
if (re.doubleValue() == 0.0) {
return formatter.format(im) + "*i";
}
return formatter.format(re) + " + i*" + formatter.format(im);
}
}
我正在审查下面的答案。 其中一个问题可能是由于
Complex num = (z.multiply(Math.atan(t))).sin();
Complex D1 = new Complex(1 + t*t).pow(z.divide(TWO));
Complex D2 = new Complex(Math.pow(Math.E, 2.0*Math.PI*t) - 1.0);
Complex den = D1.multiply(D2, MathContext.UNLIMITED);
我并没有使用
BigDecimal.pow(BigDecimal)。尽管如此,我认为这不是导致浮点数算术产生差异的直接问题。
编辑: 我尝试了Zeta函数的新积分逼近。最终,我将开发一种计算BigDecimal.pow(BigDecimal)的新方法。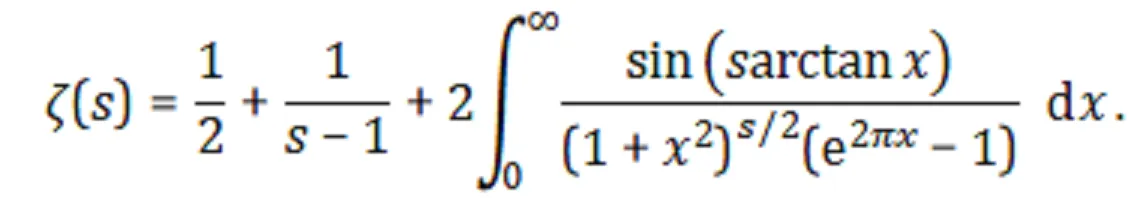
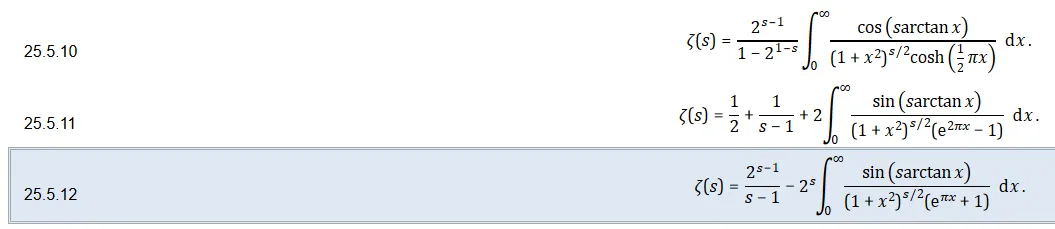
zeta(s)有什么原因吗?在我看来,还有更简单的数值方法可供选择。 - J Richard Snape