经过多年的思考,我终于找到了一个完美的解决方案!
这是一个非常直接的算法,不需要循环和近似。
以下是其工作原理:
- 计算与每个边界平面的交点时间,如果从当前点到未来点的路径穿过该平面。
- 检查每个边界的象限以进行单边界相交,返回交点。
- 确定圆形撞击的角落。
- 解决当前点、角落和相交中心(距离角落半径)之间的三角形。
- 计算时间、法线和交点中心。
现在让我们看看更详细的内容!
该函数的输入为边界(具有左、上、右、下)、当前点(起点)和未来点(终点)。
输出是称为“Intersection”的类,其中包括x、y、time、nx和ny。
- {x,y}是交点时圆心的坐标。
- time是0到1之间的值,其中0在起点,1在终点
- {nx,ny}是法线,用于反射速度以确定圆的新速度
我们首先缓存我们经常使用的变量:
float L = bounds.left;
float T = bounds.top;
float R = bounds.right;
float B = bounds.bottom;
float dx = end.x - start.x;
float dy = end.y - start.y;
计算与每个面的交点时间(如果起点和终点之间的向量穿过该平面):
float ltime = Float.MAX_VALUE;
float rtime = Float.MAX_VALUE;
float ttime = Float.MAX_VALUE;
float btime = Float.MAX_VALUE;
if (start.x - radius < L && end.x + radius > L) {
ltime = ((L - radius) - start.x) / dx;
}
if (start.x + radius > R && end.x - radius < R) {
rtime = (start.x - (R + radius)) / -dx;
}
if (start.y - radius < T && end.y + radius > T) {
ttime = ((T - radius) - start.y) / dy;
}
if (start.y + radius > B && end.y - radius < B) {
btime = (start.y - (B + radius)) / -dy;
}
现在我们要确定是否严格为侧面相撞(而不是角落相撞)。如果碰撞点位于侧面,则返回相交点:
if (ltime >= 0.0f && ltime <= 1.0f) {
float ly = dy * ltime + start.y;
if (ly >= T && ly <= B) {
return new Intersection( dx * ltime + start.x, ly, ltime, -1, 0 );
}
}
else if (rtime >= 0.0f && rtime <= 1.0f) {
float ry = dy * rtime + start.y;
if (ry >= T && ry <= B) {
return new Intersection( dx * rtime + start.x, ry, rtime, 1, 0 );
}
}
if (ttime >= 0.0f && ttime <= 1.0f) {
float tx = dx * ttime + start.x;
if (tx >= L && tx <= R) {
return new Intersection( tx, dy * ttime + start.y, ttime, 0, -1 );
}
}
else if (btime >= 0.0f && btime <= 1.0f) {
float bx = dx * btime + start.x;
if (bx >= L && bx <= R) {
return new Intersection( bx, dy * btime + start.y, btime, 0, 1 );
}
}
我们已经走到这一步,所以我们知道要么没有交点,要么与一个角碰撞。我们需要确定这个角落:
float cornerX = Float.MAX_VALUE;
float cornerY = Float.MAX_VALUE;
if (ltime != Float.MAX_VALUE) {
cornerX = L;
} else if (rtime != Float.MAX_VALUE) {
cornerX = R;
}
if (ttime != Float.MAX_VALUE) {
cornerY = T;
} else if (btime != Float.MAX_VALUE) {
cornerY = B;
}
// Account for the times where we don't pass over a side but we do hit it's corner
if (cornerX != Float.MAX_VALUE && cornerY == Float.MAX_VALUE) {
cornerY = (dy > 0.0f ? B : T);
}
if (cornerY != Float.MAX_VALUE && cornerX == Float.MAX_VALUE) {
cornerX = (dx > 0.0f ? R : L);
}
现在我们有足够的信息来解决这个三角形问题。这需要使用距离公式、找到两个向量之间的角度以及正弦定理(两次):
double inverseRadius = 1.0 / radius;
double lineLength = Math.sqrt( dx * dx + dy * dy );
double cornerdx = cornerX - start.x;
double cornerdy = cornerY - start.y;
double cornerdist = Math.sqrt( cornerdx * cornerdx + cornerdy * cornerdy );
double innerAngle = Math.acos( (cornerdx * dx + cornerdy * dy) / (lineLength * cornerdist) );
double innerAngleSin = Math.sin( innerAngle );
double angle1Sin = innerAngleSin * cornerdist * inverseRadius;
// The angle is too large, there cannot be an intersection
if (Math.abs( angle1Sin ) > 1.0f) {
return null;
}
double angle1 = Math.PI - Math.asin( angle1Sin );
double angle2 = Math.PI - innerAngle - angle1;
double intersectionDistance = radius * Math.sin( angle2 ) / innerAngleSin;
现在我们已经求出了所有的边和角度,我们可以确定时间和其他参数:
// Solve for time
float time = (float)(intersectionDistance / lineLength);
// If time is outside the boundaries, return null. This algorithm can
// return a negative time which indicates the previous intersection.
if (time > 1.0f || time < 0.0f) {
return null;
}
// Solve the intersection and normal
float ix = time * dx + start.x;
float iy = time * dy + start.y;
float nx = (float)((ix - cornerX) * inverseRadius);
float ny = (float)((iy - cornerY) * inverseRadius);
return new Intersection( ix, iy, time, nx, ny );
哇!这很有趣......就效率而言,这里有很多改进的空间。您可以重新排列侧面交叉检查,尽可能早地避免尽可能少的计算。
我希望有一种方法可以不使用三角函数来完成它,但是我必须屈服!
这是调用它并使用它来计算圆的新位置的示例,使用法线反射和交点时间计算反射的大小:
Intersection inter = handleIntersection( bounds, start, end, radius );
if (inter != null)
{
// Project Future Position
float remainingTime = 1.0f - inter.time;
float dx = end.x - start.x;
float dy = end.y - start.y;
float dot = dx * inter.nx + dy * inter.ny;
float ndx = dx - 2 * dot * inter.nx;
float ndy = dy - 2 * dot * inter.ny;
float newx = inter.x + ndx * remainingTime;
float newy = inter.y + ndy * remainingTime;
// new circle position = {newx, newy}
}
我已经在pastebin上发布了完整的代码,提供一个完全交互式示例,您可以绘制起点和终点,它会显示您的时间和矩形反弹结果。
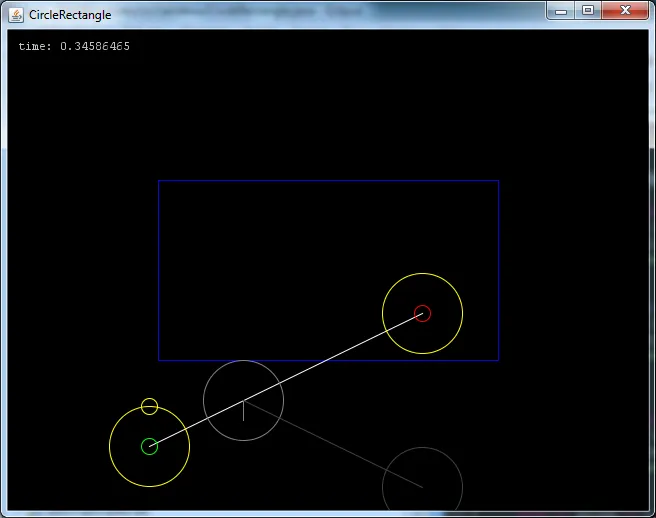
如果您想立即运行它,您必须从我的博客下载代码,否则将其放入您自己的Java2D应用程序中。
编辑: 我修改了pastebin中的代码,还包括碰撞点,并进行了一些速度改进。
编辑: 您可以通过使用矩形的角度来取消旋转带有圆形起始点和结束点的矩形。您将执行交集检查,然后旋转结果点和法线。
编辑: 我修改了pastebin上的代码,使其在圆形路径的边界体积与矩形不相交时提前退出。
3
找到接触时刻并不太难:
你需要在碰撞之前(B)和之后(A)的时间步骤中获取圆和矩形的位置。计算圆心到矩形与其相撞的线的距离,即在时间A和B时的距离(即,点到直线的常见公式),然后碰撞的时间是:
tC = dt*(dB-R)/(dA+dB),
其中tC是碰撞时间,dt是时间步长,dB是碰撞前到线的距离,dA是碰撞后的距离,R是圆的半径。
这假设一切都是局部线性的,也就是说,您的时间步长足够小,因此在计算碰撞的时间步长中,速度等几乎不会改变。这就是时间步长的意义所在:当步长足够小时,非线性问题变成了局部线性问题。在上面的方程中,我利用了这一点:dB-R是圆与线之间的距离,dA+dB是总移动距离,因此这个问题只是将距离比率等同于时间比率,假设在时间步长内一切都是近似线性的(当然,在碰撞瞬间,线性逼近并不是最好的,但为了找到碰撞瞬间,问题是是否在碰撞瞬间之前的时间步长内是线性的)。
这是一个非线性问题,对吧?
你需要采取时间步长,并通过在步骤开始时计算的速度来移动球的位移。如果发现重叠,减小步长并重新计算直到收敛。
你是否假设球和矩形都是刚体,没有变形?无摩擦接触?接触后如何处理球的运动?你会转换到接触的坐标系(法向量+切向量)进行计算,然后再转换回来吗?
这不是一个简单的问题。
也许你应该考虑使用物理引擎,比如Box2D,而不是自己编写代码。
4
原文链接
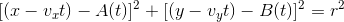
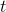 是一个数字,回答了这个问题:多少帧之前发生了完美的碰撞?
是一个数字,回答了这个问题:多少帧之前发生了完美的碰撞? 是圆的半径。
是圆的半径。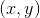 是圆心。
是圆心。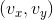 是它的速度。
是它的速度。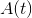 和
和 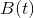 是函数,返回圆与矩形碰撞的点的x和y坐标(当圆处于
是函数,返回圆与矩形碰撞的点的x和y坐标(当圆处于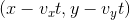 位置时,也就是完美地与矩形碰撞的位置)。
位置时,也就是完美地与矩形碰撞的位置)。