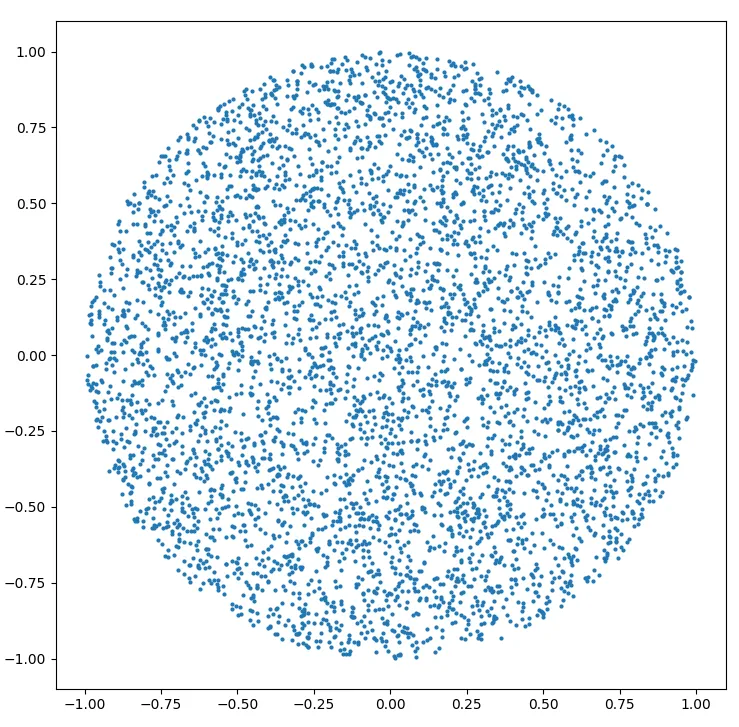
在圆内均匀生成一个随机点
9
如何在半径为R的圆内生成随机点：
r = R * sqrt(random())
theta = random() * 2 * PI
（假设
random()均匀地给出0到1之间的值）如果你想将其转换为笛卡尔坐标，可以执行
x = centerX + r * cos(theta)
y = centerY + r * sin(theta)
为什么要用sqrt(random())？
让我们来看一下导致sqrt(random())的数学原理。为了简单起见，假设我们正在处理单位圆，即R=1。
无论我们从中心点往外看多远，点之间的平均距离应该是相同的。这意味着例如，在周长为2的圆上查找时，我们应该找到比周长为1的圆上的点数多一倍的点。
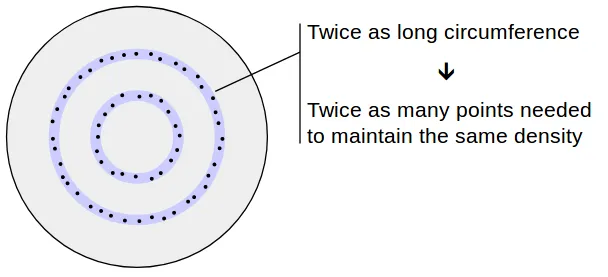
由于圆的周长（2πr）随着 r 线性增长，因此随机点的数量也应该随着 r 线性增长。换句话说，所需的 概率密度函数 (PDF) 线性增长。由于 PDF 应该具有面积为 1 并且最大半径为 1，因此我们有
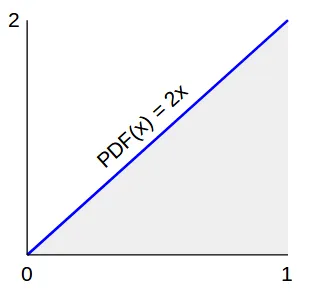
- 从概率密度函数（PDF）中创建累积分布函数（CDF）
- 沿着y=x镜像
- 将所得函数应用于介于0和1之间的均匀值。
假设我们想生成一个符合以下分布的随机点：
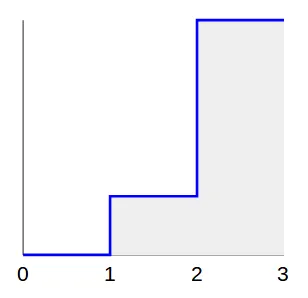即
1/5的点在1和2之间均匀分布，以及
4/5的点在2和3之间均匀分布。
CDF是PDF的累积版本，顾名思义。直观地说：虽然PDF（x）描述了x处的随机值的数量，但CDF（x）描述了小于x的随机值的数量。
在这种情况下，CDF将如下所示：
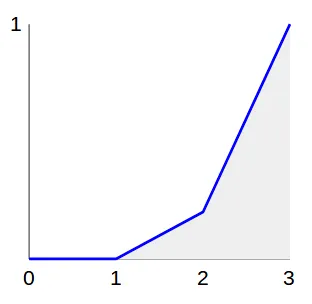为了看到这有多有用，想象一下我们从左到右以均匀分布的高度射出子弹。当子弹击中线时，它们会掉落到地面上：
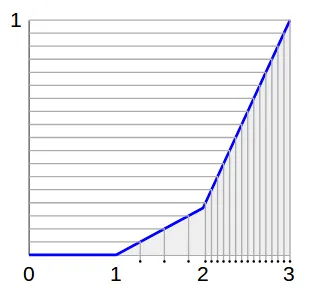看到子弹在地面上的密度与我们想要的分布相对应！我们就快成功了！
问题在于对于这个函数，y轴是输出，而x轴是输入。我们只能“从地面向上射子弹”！我们需要反函数！
这就是为什么我们要镜像整个过程；x变成y，y变成x：
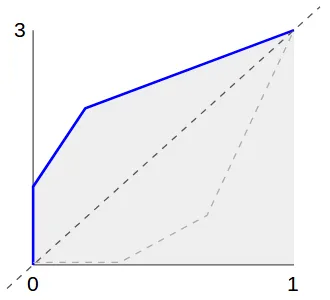我们称之为CDF-1。要根据所需分布获取值，我们使用CDF-1（random()）。
...所以，回到生成随机半径值的问题，其中我们的PDF等于2x。
步骤1：创建CDF：
由于我们正在处理实数，因此CDF表示为PDF的积分。
CDF(x) = ∫ 2x = x2
步骤2：沿着y=x镜像CDF：
从数学上讲，这归结为交换x和y并解决y的问题：
CDF: y = x2
交换: x = y2
解决: y = √x
CDF-1: y = √x
步骤3：将得到的函数应用于0到1之间的均匀值
CDF-1(random()) = √random()
这就是我们要推导的内容 :-)
6
random(min_radius², max_radius²) 时，你是指与 random() * (max_radius² - min_radius²) + min_radius² 等效的内容，其中 random() 返回0到1之间的均匀值吗？ - aioobe现在考虑一个圆。在极限情况下，我们可以将其视为无数个等腰三角形ABC，其中B位于原点，A和C在圆周上非常接近。我们可以通过选择一个角度theta来选择其中之一。因此，我们现在需要通过在银片ABC中选择一个点来生成距离中心的距离。同样，将其扩展到ABCD，其中D现在是从圆心到半径的两倍。
使用上述方法在ABCD中选择一个随机点很容易。在AB上选择一个随机点。在BC上均匀选择一个随机点。即在[0，R]上均匀选择一对随机数字x和y，给出距离中心的距离。我们的三角形是一个狭窄的银片，因此AB和BC基本上是平行的。因此，点Z就是距离原点x+y。如果x+y>R，则折叠回来。
这是R=1的完整算法。我希望您同意它非常简单。它使用三角函数，但是与拒绝抽样不同，您可以保证它需要多长时间以及需要多少次random（）调用。
t = 2*pi*random()
u = random()+random()
r = if u>1 then 2-u else u
[r*cos(t), r*sin(t)]
这是Mathematica中的代码。
f[] := Block[{u, t, r},
u = Random[] + Random[];
t = Random[] 2 Pi;
r = If[u > 1, 2 - u, u];
{r Cos[t], r Sin[t]}
]
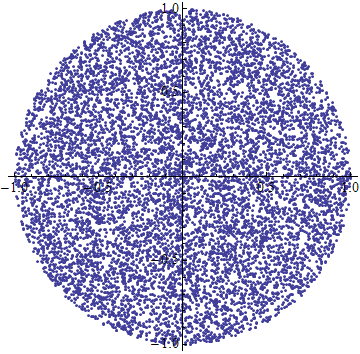
ListPlot[Table[f[], {10000}], AspectRatio -> Automatic]
21
random()+random()+random()和一些更复杂的折叠（即将无限薄的平行六面体折叠成四面体）。不确定这是否是一个好方法。 - sigfpe这里有一个快速简单的解决方案。
在范围（0，1）内选择两个随机数，即a和b。 如果b < a，则交换它们。 你的点是(b*R*cos(2*pi*a/b), b*R*sin(2*pi*a/b))。
你可以将这个解决方案想象成如下形式。如果你把圆切开，然后拉直，你就会得到一个直角三角形。缩小该三角形，你会得到从(0,0)到(1,0)再到(1,1)最后回到(0,0)的三角形。所有这些转换都统一地改变了密度。你所做的就是在三角形中均匀地选择一个随机点，并反转过程以在圆中得到一个点。
10
float random1 = MathUtils.random();
float random2 = MathUtils.random();
float randomXPoint = random2*radius*MathUtils.cos(MathUtils.PI2*random1/random2);
float randomYPoint = random2*radius*MathUtils.sin(MathUtils.PI2*random1/random2); - Toni Alvarez注意点密度与半径的平方成反比，因此不要从[0, r_max]中选取r，而是从[0, r_max^2]中选取，然后按以下方式计算您的坐标：
请注意，在半径较小的区域内将会有更多的点，而在半径较大的区域内将会有更少的点。
x = sqrt(r) * cos(angle)
y = sqrt(r) * sin(angle)
这将在圆盘上给您均匀的点分布。
这样来想一下：如果你有一个矩形，其中一个轴是半径，另一个轴是角度，并且你取在该矩形内靠近半径为0的点。 这些点将全部非常接近原点（即在圆上彼此靠近）。 然而，靠近半径R的点，这些将全部靠近圆的边缘（即相互之间远离很多）。
这可能会让你对为什么会出现这种行为有些想法。
那个链接中得出的因子告诉你，在映射到圆后，需要调整矩形中相应区域的面积，以不依赖于半径。
编辑：因此他在你分享的链接中写的是，“通过计算累积分布的反函数就可以很容易做到这一点，我们得到了r:”。
基本前提是，您可以通过将均匀变量映射到所需概率密度函数的累积分布函数的反函数来创建具有所需分布的变量。为什么？暂且不论，但这是事实。
这里是我对数学的某种直观解释。密度函数f(r)与r的关系必须成比例。理解这个事实是任何基本微积分书籍的一部分。请参见极坐标区域元素部分。其他一些帖子也提到了这一点。
因此，我们将其称为f(r) = C * r;
这最终成为了大部分工作。现在，由于f(r)应该是概率密度，您可以很容易地看出，通过对区间（0，R）中的f(r)进行积分，您将得到C = 2/R^2（这是给读者的练习题）。
因此，f(r) = 2 * r / R^2
好的，那就是你得到链接中的公式的方法。
然后，最后一部分是从（0,1）中的均匀随机变量u转换，必须通过所需密度f(r)的累积分布函数的反函数来映射。要理解为什么会发生这种情况，您需要找到像Papoulis这样的高级概率文本（或自己推导）。
将 f(r) 进行积分，得到 F(r) = r^2/R^2。
要找到其反函数，先令 u = r^2/R^2，然后解出 r，得到 r = R * sqrt(u)。
这在直觉上也是有意义的，因为当 u = 0 时，r 应该映射到 0。同样地，当 u = 1 时，r 应该映射到 R。此外，它还遵循平方根函数，这也是合理的，并且与链接相匹配。
假设 ρ (半径) 和 φ (极角) 是一个圆内任意一点的极坐标对应的随机变量。如果这些点是均匀分布的，那么ρ和φ的分布函数是什么？
对于任何r: 0 < r < R，半径坐标ρ小于r的概率为
P[ρ < r] = P[点在半径为r的圆内] = S1 / S0 =(r/R)2
其中S1和S0分别是半径为r和R的圆的面积。因此，累积分布函数可以表示为：
0 if r<=0
CDF = (r/R)**2 if 0 < r <= R
1 if r > R
并且PDF:
PDF = d/dr(CDF) = 2 * (r/R**2) (0 < r <= R).
请注意，当R=1时，随机变量sqrt(X)（其中X在[0,1)上均匀分布）具有这个确切的累积分布函数（因为P[sqrt(X) <y] = P[x < y**2] = y**2，对于0<y<= 1）。
φ的分布显然是从0到2*π均匀的。现在您可以创建随机极坐标并使用三角方程将其转换为笛卡尔坐标：
x = ρ * cos(φ)
y = ρ * sin(φ)
无法抵制发布R=1的Python代码。
from matplotlib import pyplot as plt
import numpy as np
rho = np.sqrt(np.random.uniform(0, 1, 5000))
phi = np.random.uniform(0, 2*np.pi, 5000)
x = rho * np.cos(phi)
y = rho * np.sin(phi)
plt.scatter(x, y, s = 4)
你将会得到：
因此，我们希望半径概率密度具有以下属性：
选择小于或等于给定半径 r 的概率必须与半径为 r 的圆的面积成比例。（因为我们希望在点上具有均匀分布而较大的区域意味着更多的点）
换句话说，我们希望选择[0，r]之间的半径的概率等于其在整个圆中的总面积的份额。总圆面积为 pi*R^2，半径为 r 的圆的面积为 pi*r^2。因此，我们希望选择[0，r]之间的半径的概率为(pi*r^2)/(pi*R^2) = r^2/R^2。
现在来看一下数学：选择[0，r]之间的半径的概率是从 0 到 r 的 p(r) dr 的积分（这只是因为我们将所有较小半径的概率相加）。因此，我们希望积分(p(r)dr) = r^2/R^2。我们可以清楚地看到 R^2 是一个常数，因此我们需要做的就是找出哪个 p(r) 在积分时会给我们类似于 r^2 的东西。答案显然是 r * 常数。积分(r * 常数 dr) = r^2/2 * 常数。这必须等于 r^2/R^2，因此常数 = 2/R^2。因此，您有概率分布 p(r) = r * 2/R^2
注意： 另一种更直观的解决问题的方式是想象你正在尝试为每个半径为r的圆形赋予等于其周长上点数比例的概率密度。因此，一个具有半径r的圆将在其周长上拥有2 * pi * r个“点”。点的总数是pi * R^2。因此，你应该给半径为r的圆赋予等于(2 * pi * r) / (pi * R^2) = 2 * r/R^2的概率。这种方法更容易理解，更直观，但数学上不太严谨。
根据你选择点的方式，分布可能会有所不同，即使它们在某种意义上是均匀随机的。
这篇博客似乎试图以以下方式使其均匀随机：如果你取圆的子圆，中心相同，则点落在该区域内的概率与该区域的面积成比例。我相信，这是试图遵循现在标准的解释，即对于带有定义面积的2D区域，“均匀随机”的概率是点落在任何区域（面积定义良好）的面积成比例。
2
这里是我用Python生成从半径为rad的圆中产生num个随机点的代码：
import matplotlib.pyplot as plt
import numpy as np
rad = 10
num = 1000
t = np.random.uniform(0.0, 2.0*np.pi, num)
r = rad * np.sqrt(np.random.uniform(0.0, 1.0, num))
x = r * np.cos(t)
y = r * np.sin(t)
plt.plot(x, y, "ro", ms=1)
plt.axis([-15, 15, -15, 15])
plt.show()
1
r = np.sqrt(np.random.uniform(0.0, rad**2, num))？ - user2508324我认为在这种情况下使用极坐标会使问题变得复杂，如果你从边长为2R的正方形中随机选取点，然后选择满足x^2+y^2<=R^2的点(x,y)，那么问题会更容易解决。
4
原文链接