这里的二叉树不一定是二叉搜索树。
可以将其结构表示为 -
struct node {
int data;
struct node *left;
struct node *right;
};
其中序遍历结果为：8，4，9，2，5，1，6，3，7
后序遍历结果为：8，9，4，5，2，6，7，3，1
例如，如果我们要找到节点8和5的公共祖先，则需要在中序遍历时列出所有位于8和5之间的节点，而在此示例中，它们是[4，9，2]。然后我们检查此列表中最后出现在后序遍历中的节点，即2。因此，8和5的公共祖先是2。
我认为该算法的复杂度为O（n）（中序/后序遍历的O（n），其余步骤再次为O（n），因为它们仅是数组中的简单迭代）。但很有可能我错了。:-)
但这只是一个非常粗略的方法，我不确定是否有一些情况会失效。还有其他（可能更优）的解决方案吗？
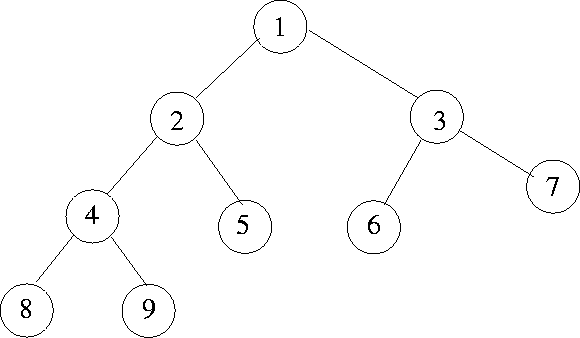
从root节点开始向下移动，如果找到任何一个节点，它的直接子节点是p或q，那么这个节点就是LCA。 如果p或q是节点的值，则返回该节点。否则，当p或q之一是另一个的直接子节点时，将无法成功。
否则，如果在其右（或左）子树中找到具有p的节点和在其左（或右）子树中找到具有q的节点，则该节点是LCA。
修复后的代码如下：
treeNodePtr findLCA(treeNodePtr root, treeNodePtr p, treeNodePtr q) {
// no root no LCA.
if(!root) {
return NULL;
}
// if either p or q is the root then root is LCA.
if(root==p || root==q) {
return root;
} else {
// get LCA of p and q in left subtree.
treeNodePtr l=findLCA(root->left , p , q);
// get LCA of p and q in right subtree.
treeNodePtr r=findLCA(root->right , p, q);
// if one of p or q is in leftsubtree and other is in right
// then root it the LCA.
if(l && r) {
return root;
}
// else if l is not null, l is LCA.
else if(l) {
return l;
} else {
return r;
}
}
}
treeNodePtr findLCA(treeNodePtr root, treeNodePtr p, treeNodePtr q) {
// no root no LCA.
if(!root) {
return NULL;
}
// if either p or q is direct child of root then root is LCA.
if(root->left==p || root->left==q ||
root->right ==p || root->right ==q) {
return root;
} else {
// get LCA of p and q in left subtree.
treeNodePtr l=findLCA(root->left , p , q);
// get LCA of p and q in right subtree.
treeNodePtr r=findLCA(root->right , p, q);
// if one of p or q is in leftsubtree and other is in right
// then root it the LCA.
if(l && r) {
return root;
}
// else if l is not null, l is LCA.
else if(l) {
return l;
} else {
return r;
}
}
}
Nick Johnson说如果没有父指针，O(n)时间复杂度算法是最好的。要查看该算法的简单递归版本，请参见Kinding's post中的代码，它以O(n)的时间运行。
但请记住，如果您的节点有父指针，则可能存在改进的算法。对于两个问题中的节点，请构造一个包含从根到节点的路径的列表，方法是从节点开始，并在前面插入父节点。
因此，对于您的示例中的8，您将获得（显示步骤）：{4}，{2, 4}，{1，2，4}
对于您要查询的另一个节点执行相同的操作，结果为（未显示步骤）：{1, 2}
现在比较您制作的两个列表，查找列表不同的第一个元素或其中一个列表的最后一个元素，以先出现的为准。
该算法需要O(h)时间，其中h是树的高度。在最坏的情况下，O(h)等价于O(n)，但如果树是平衡的，则仅为O(log(n))。它还需要O(h)空间。可以使用仅使用常量空间的改进版本，其代码显示在CEGRD's post中。
O(h)仅为O(log(n))。对于任何树，无论是二叉还是非二叉，如果您有父节点指针，则可以通过跟随父节点指针最多h次来在O(h)时间内确定从叶到根的路径。这将给您从叶子到根的路径。如果将路径存储为堆栈，则迭代堆栈将为您提供从根到叶子的路径。如果缺少父节点指针，并且树没有特殊结构，则找到从根到叶子的路径需要O(n)时间。 - Kevin Cathcart以下是JAVA的工作代码
public static Node LCA(Node root, Node a, Node b) {
if (root == null) {
return null;
}
// If the root is one of a or b, then it is the LCA
if (root == a || root == b) {
return root;
}
Node left = LCA(root.left, a, b);
Node right = LCA(root.right, a, b);
// If both nodes lie in left or right then their LCA is in left or right,
// Otherwise root is their LCA
if (left != null && right != null) {
return root;
}
return (left != null) ? left : right;
}
到目前为止给出的答案使用递归或存储路径在内存中等方式。
这两种方法可能会因为树的深度太大而失败。
以下是我对此问题的看法。当我们检查两个节点的深度（距离根的距离）时，如果它们相等，那么我们可以安全地从两个节点向上移动，直到共同祖先。如果其中一个深度更大，则我们应该从深层节点向上移动，同时保持在另一个节点。
以下是代码：
findLowestCommonAncestor(v,w):
depth_vv = depth(v);
depth_ww = depth(w);
vv = v;
ww = w;
while( depth_vv != depth_ww ) {
if ( depth_vv > depth_ww ) {
vv = parent(vv);
depth_vv--;
else {
ww = parent(ww);
depth_ww--;
}
}
while( vv != ww ) {
vv = parent(vv);
ww = parent(ww);
}
return vv;
该算法的时间复杂度为：O(n)。算法的空间复杂度为：O(1)。
关于深度的计算，我们可以先记住定义：如果v是根，则depth(v) = 0；否则，depth(v) = depth(parent(v)) + 1。我们可以按照以下方法计算深度：
depth(v):
int d = 0;
vv = v;
while ( vv is not root ) {
vv = parent(vv);
d++;
}
return d;
tree_node_type *LowestCommonAncestor(
tree_node_type *root , tree_node_type *p , tree_node_type *q)
{
tree_node_type *l , *r , *temp;
if(root==NULL)
{
return NULL;
}
if(root->left==p || root->left==q || root->right ==p || root->right ==q)
{
return root;
}
else
{
l=LowestCommonAncestor(root->left , p , q);
r=LowestCommonAncestor(root->right , p, q);
if(l!=NULL && r!=NULL)
{
return root;
}
else
{
temp = (l!=NULL)?l:r;
return temp;
}
}
}
这有点取决于你的二叉树结构。假设你有一种方法可以在给定根节点的情况下找到所需的叶节点-只需将其应用于两个值，直到所选择的分支分歧。
如果没有办法在给定根节点的情况下找到所需的叶节点，则你唯一的解决方案-无论是正常操作还是查找最后一个公共节点-都是对树进行暴力搜索。
查找两个节点的共同祖先：
这适用于二叉搜索树。
//find the search node below root
bool findNode(node* root, node* search)
{
//base case
if(root == NULL)
return false;
if(root->val == search->val)
return true;
//search for the node in the left and right subtrees, if found in either return true
return (findNode(root->left, search) || findNode(root->right, search));
}
//returns the LCA, n1 & n2 are the 2 nodes for which we are
//establishing the LCA for
node* getLCA(node* root, node* n1, node* n2)
{
//base case
if(root == NULL)
return NULL;
//If 1 of the nodes is the root then the root is the LCA
//no need to recurse.
if(n1 == root || n2 == root)
return root;
//check on which side of the root n1 and n2 reside
bool n1OnLeft = findNode(root->left, n1);
bool n2OnLeft = findNode(root->left, n2);
//n1 & n2 are on different sides of the root, so root is the LCA
if(n1OnLeft != n2OnLeft)
return root;
//if both n1 & n2 are on the left of the root traverse left sub tree only
//to find the node where n1 & n2 diverge otherwise traverse right subtree
if(n1OnLeft)
return getLCA(root->left, n1, n2);
else
return getLCA(root->right, n1, n2);
}