这是另一个需要先审慎分析后编写代码的问题。
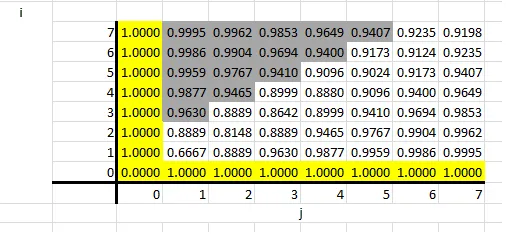
我认为你应该首先查看数字的网格,而不是将它们表示为小数,而是改用分数。
显而易见的第一件事是,您所拥有的
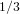
的总数仅是从原点
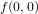
的距离度量。
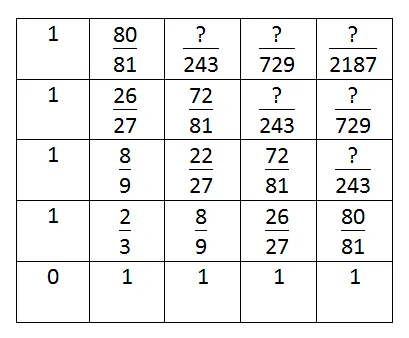
如果您以这种方式查看网格,则可以获得所有分母:

请注意,第一行和第一列并不全为“1”——它们被选中以遵循模式和适用于所有其他正方形的一般公式。
分子有点棘手,但仍然可行。与大多数类似的问题一样,答案与组合、阶乘以及更复杂的事物有关。典型的条目包括
卡特兰数、
斯特林数、
帕斯卡三角形,你几乎总会看到使用
超几何函数。
除非你做了很多数学,否则你不太可能熟悉所有这些,而且有大量的文献。因此,我有一个更容易找到所需关系的方法,几乎总是有效的。它是这样的:
- 编写一个朴素且低效的算法来获取您想要的序列。
- 将相当大量的数字复制到Google中。
希望整数序列在线百科全书 中出现结果。
3.b. 如果没有,则查看您的序列中的某些差异或与您的数据相关的其他序列。
使用找到的信息来实现所述序列。
因此,按照这种逻辑,这里是分子:
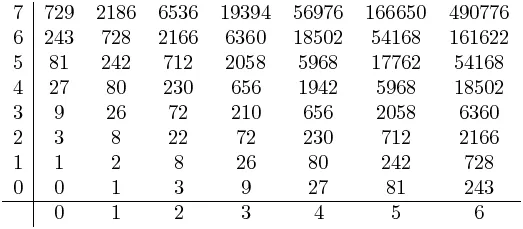
很不幸,用谷歌搜索这些内容没有得到任何结果。但是,你可以注意到它们有一些共同点,其中最主要的是第一行/列只是3的幂,并且第二行/列比三的幂小1。这种边界正好与帕斯卡三角形和许多相关序列相同。
以下是分子和分母之间差异的矩阵:
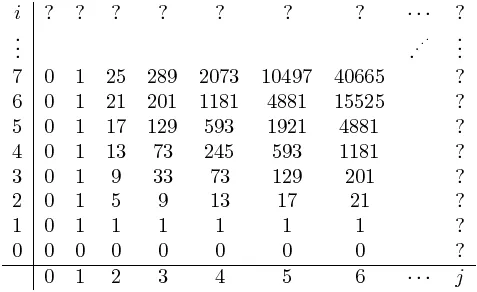
我们决定f(0,0)元素将遵循相同的模式。这些数字看起来已经简单了许多。还要注意一点 - 有趣的是,这些数字遵循与初始数字相同的规则 - 只是第一个数字是1(它们偏移了一列和一行)。T(i,j)=T(i-1,j)+T(i,j-1)+3*T(i-1,j-1)
1
1 1
1 5 1
1 9 9 1
1 13 33 13 1
1 17 73 73 17 1
1 21 129 245 192 21 1
1 25 201 593 593 201 25 1
这更像是组合数学中经常看到的序列。
如果你用这个矩阵中的数字搜索谷歌,你会得到一个结果。
然后,如果你去掉原始数据的链接,你会得到序列
A081578,它被描述为“Pascal-(1,3,1)数组”,这很有意义——如果你旋转矩阵,使
0,0元素在顶部,并且元素形成一个三角形,那么你取左侧元素的
1*,上方元素的
3*和右侧元素的
1*。
现在的问题是实现用于生成数字的公式。
很不幸,这通常说起来比做起来更容易。例如,页面上给出的公式:
T(n,k)=sum{j=0..n, C(k,j-k)*C(n+k-j,k)*3^(j-k)}
是错误的,需要读一些内容(页面上链接了
该论文)才能找到正确的公式。您需要查看命题26和推论28。在命题13之后的表2中提到了该序列。请注意
r=4。
正确的公式在命题26中给出,但那里也有一个错别字:求和符号中的
k=0应为
j=0。
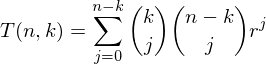
其中T是包含系数的三角矩阵。
OEIS页面提供了一些计算这些数字的实现,但它们都不是用Java编写的,也不能轻松地转换为Java:
这里有一个Mathematica示例:
Table[ Hypergeometric2F1[-k, k-n, 1, 4], {n, 0, 10}, {k, 0, n}]
一如既往地简明扼要。同时也有一个 Haskell 版本,同样简洁。
a081578 n k = a081578_tabl !! n !! k
a081578_row n = a081578_tabl !! n
a081578_tabl = map fst $ iterate
(\(us, vs) -> (vs, zipWith (+) (map (* 3) ([0] ++ us ++ [0])) $
zipWith (+) ([0] ++ vs) (vs ++ [0]))) ([1], [1, 1])
我知道你是用Java编写的,但我懒得把我的答案转换成Java(抱歉)。这是一个Python实现:
from __future__ import division
import math
def cache(function):
cachedResults = {}
def wrapper(*args):
if args in cachedResults:
return cachedResults[args]
else:
result = function(*args)
cachedResults[args] = result
return result
return wrapper
@cache
def fact(n):
return math.factorial(n)
@cache
def binomial(n,k):
if n < k: return 0
return fact(n) / ( fact(k) * fact(n-k) )
def numerator(i,j):
"""
Naive way to calculate numerator
"""
if i == j == 0:
return 0
elif i == 0 or j == 0:
return 3**(max(i,j)-1)
else:
return numerator(i-1,j) + numerator(i,j-1) + 3*numerator(i-1,j-1)
def denominator(i,j):
return 3**(i+j-1)
def A081578(n,k):
"""
http://oeis.org/A081578
"""
total = 0
for j in range(n-k+1):
total += binomial(k, j) * binomial(n-k, j) * 4**(j)
return int(total)
def diff(i,j):
"""
Difference between the numerator, and the denominator.
Answer will then be 1-diff/denom.
"""
if i == j == 0:
return 1/3
elif i==0 or j==0:
return 0
else:
return A081578(j+i-2,i-1)
def answer(i,j):
return 1 - diff(i,j) / denominator(i,j)
N, M = 10,10
for i in range(N):
row = "%10.5f"*M % tuple([numerator(i,j)/denominator(i,j) for j in range(M)])
print row
print ""
for i in range(N):
row = "%10.5f"*M % tuple([answer(i,j) for j in range(M)])
print row
所以,对于一个闭合形式:
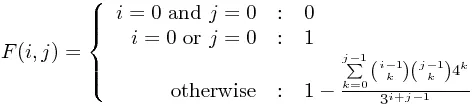
这里的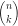 只是二项式系数。
只是二项式系数。
以下是结果:
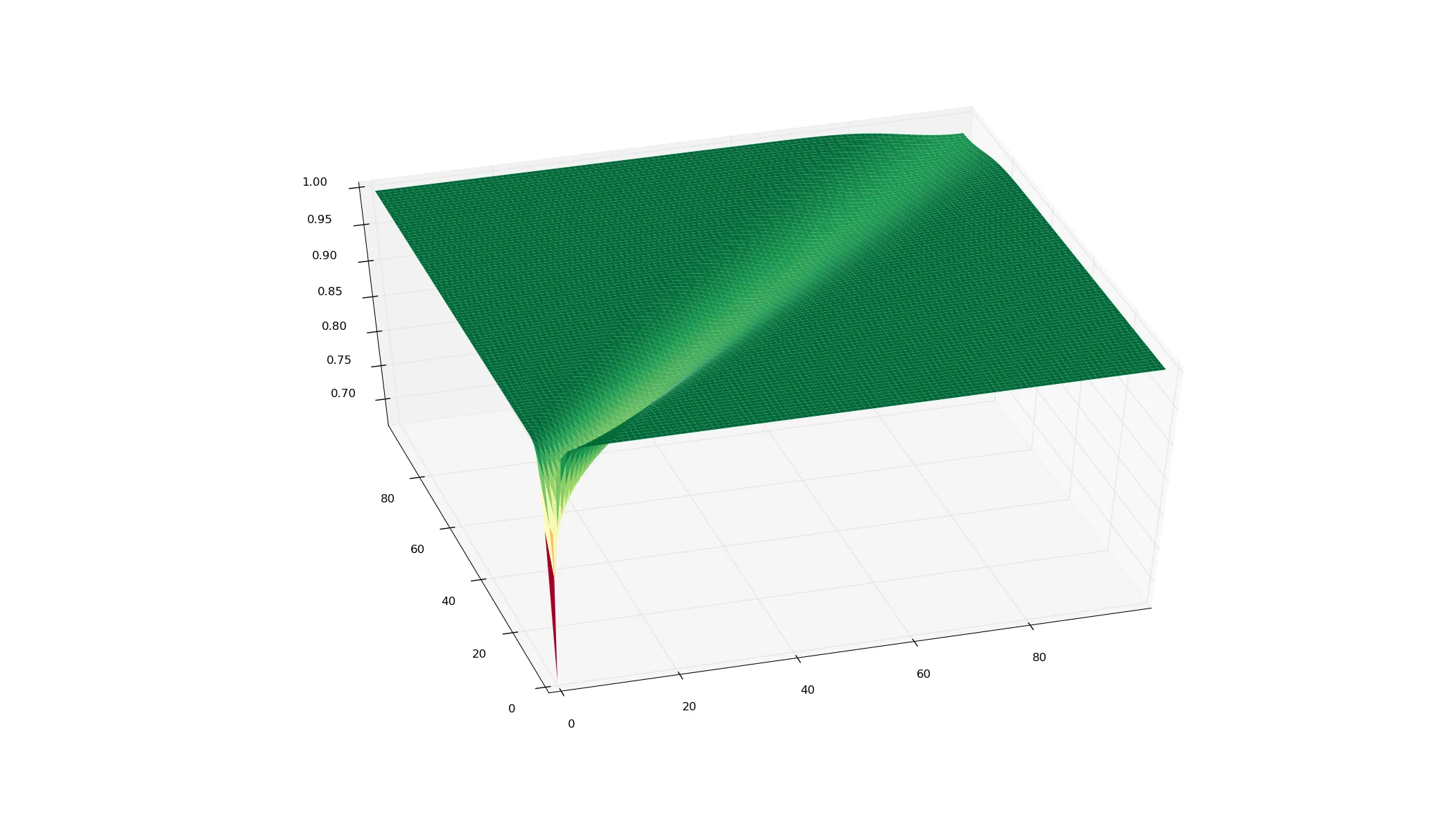
如果您想处理大量数据,那么您需要以不同的方式计算二项式系数,否则整数会溢出。但您的答案应该是浮点数。因为您似乎对大的
f(n) = T(n,n) 感兴趣,所以可以使用 Stirling 近似公式或其他方法。
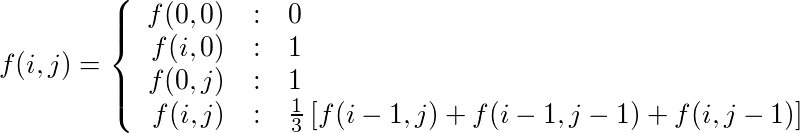
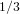 的总数仅是从原点
的总数仅是从原点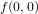 的距离度量。
的距离度量。


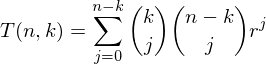
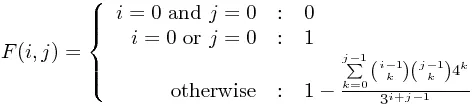
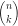 只是二项式系数。
只是二项式系数。
NxN的矩阵,你无法实现O(N)! - user1196549[0 N]x [0 N]中所有值的f还是其中的一些或仅一个? - user1196549