使用FFTW3库在FORTRAN中评估高斯函数的快速傅里叶变换

Question

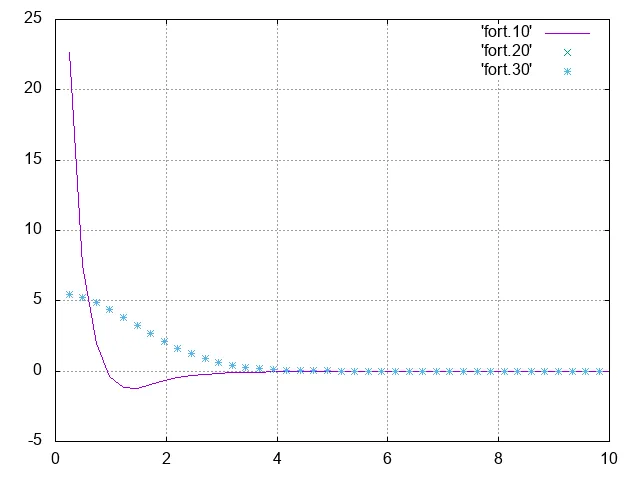
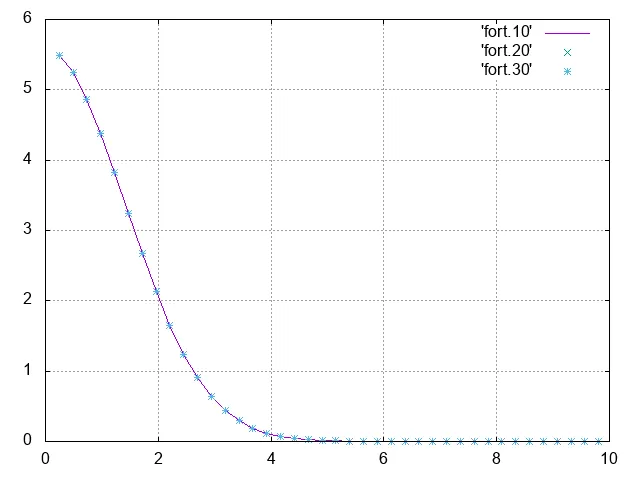
我正在尝试编写一段FORTRAN代码，使用FFTW3库计算高斯函数 f(r)=exp(-(r^2)) 的快速傅里叶变换。众所周知，高斯函数的傅里叶变换是另一个高斯函数。

我考虑在球坐标中计算高斯函数的傅里叶变换积分。

因此，得到的积分可以简化为[r*exp(-(r^2))*sin(kr)]dr的积分。

我编写了以下FORTRAN代码，用于评估由纯实数输入数组执行的离散正弦变换DST，其中DST通过FFTW3中现有的C_FFTW_RODFT00执行，考虑到位置空间中的离散值为r=i*delta (i=1,2,...,1024)，而DST的输入数组为函数r*exp(-(r^2))而不是高斯函数。积分[r*exp(-(r^2))*sin(kr)]dr中的正弦函数是由对球坐标的积分导致的，并且它不是一般情况下进行解析傅里叶变换时出现的exp(ik.r)的虚部。

然而，结果在动量空间中不是高斯函数。

Module FFTW3
 use, intrinsic :: iso_c_binding
include 'fftw3.f03'
end module  

program sine_FFT_transform
use FFTW3
implicit none
integer, parameter :: dp=selected_real_kind(8)

real(kind=dp), parameter :: pi=acos(-1.0_dp)
integer, parameter :: n=1024 
real(kind=dp) :: delta, k
real(kind=dp) :: numerical_F_transform
integer :: i
type(C_PTR) ::  my_plan
real(C_DOUBLE), dimension(1024) :: y
real(C_DOUBLE), dimension(1024) :: yy, yk
integer(C_FFTW_R2R_KIND) :: C_FFTW_RODFT00

my_plan= fftw_plan_r2r_1d(1024,y,yy,FFTW_FORWARD, FFTW_ESTIMATE)

delta=0.0125_dp
do i=1, n        !inserting the input one-dimension position function
y(i)= 2*(delta)*(i-1)*exp(-((i-1)*delta)**2) 
! I multiplied by 2 due to the definition of C_FFTW_RODFT00 in FFTW3
end do

call fftw_execute_r2r(my_plan, y,yy)   
do i=2, n
k = (i-1)*pi/n/delta 
yk(i) = 4*pi*delta*yy(i)/2  !I divide by 2 due to the definition of 
                            !C_FFTW_RODFT00
numerical_F_transform=yk(i)/k
write(11,*) i,k,numerical_F_transform
end do
call fftw_destroy_plan(my_plan)

end program 

执行上述代码将生成如下图所示，该图不是高斯函数的结果。 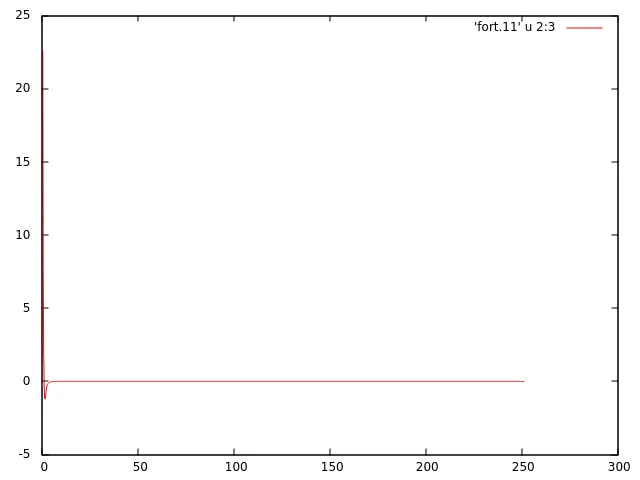有人能帮我理解问题出在哪里吗？我猜问题主要是由于FFTW3引起的。也许我在边界条件上没有正确使用它。

- Mohammed Alhissi

---

你好，你的函数缺少绘图，这使得回答变得困难，就像坐在公交车上一样。但我发现两个有点奇怪的地方，一个是roygvib提到的，你用yk创建了计划(plan)，但在转换(transform)中使用了yy；另一个是对于频率，虽然你的版本并没有错，但更常见的方式是将范围的后半部分作为负频率——这样，如果你做了正确的FFT，绘图看起来会像一个高斯曲线，而你所做的不会（它将是两个“1/2高斯曲线”，分别在范围的两端）。 - Ian Bush

感谢roygvib和Ian Bush。你们的回答很有帮助。负频率没有问题，只要正频率正确就可以生成。在编辑代码后，图形仍然存在负变换，这不会使绘图成为高斯分布。问题仍然存在!!!! - Mohammed Alhissi

Answer 1

浏览FFTW网站上的相关页面（实数变换，变换类型，实数奇变换（DST））以及Fortran的头文件，看起来FFTW希望使用FFTW_RODFT00等而不是FFTW_FORWARD来指定实数变换的类型。例如：

! my_plan= fftw_plan_r2r_1d( n, y, yy, FFTW_FORWARD, FFTW_ESTIMATE )
my_plan= fftw_plan_r2r_1d( n, y, yy, FFTW_RODFT00, FFTW_ESTIMATE )

对上述页面中展示的“type-I”离散正弦变换（DST-I）进行操作。该修改似乎解决了问题（即，使傅里叶变换成为具有正值的高斯函数）。

---

以下是OP代码的略微修改版本，以实验上述修改：

! ... only the modified part is shown...
real(dp) :: delta, k, r, fftw, num, ana
integer :: i, j, n
type(C_PTR) ::  my_plan
real(C_DOUBLE), allocatable :: y(:), yy(:)

delta = 0.0125_dp ; n = 1024   ! rmax = 12.8
! delta = 0.1_dp    ; n = 128    ! rmax = 12.8
! delta = 0.2_dp    ; n = 64    ! rmax = 12.8
! delta = 0.4_dp    ; n = 32    ! rmax = 12.8

allocate( y( n ), yy( n ) )

! my_plan= fftw_plan_r2r_1d( n, y, yy, FFTW_FORWARD, FFTW_ESTIMATE )
my_plan= fftw_plan_r2r_1d( n, y, yy, FFTW_RODFT00, FFTW_ESTIMATE )

! Loop over r-grid
do i = 1, n
    r = i * delta              ! (2-a)
    y( i )= r * exp( -r**2 )
end do

call fftw_execute_r2r( my_plan, y, yy )

! Loop over k-grid
do i = 1, n

    ! Result of FFTW
    k = i * pi / ((n + 1) * delta)    ! (2-b)
    fftw = 4 * pi * delta * yy( i ) / k / 2   ! the last 2 due to RODFT00

    ! Numerical result via quadrature
    num = 0
    do j = 1, n
        r = j * delta
        num = num + r * exp( -r**2 ) * sin( k * r )
    enddo
    num = num * 4 * pi * delta / k

    ! Analytical result
    ana = sqrt( pi )**3 * exp( -k**2 / 4 )

    ! Output
    write(10,*) k, fftw
    write(20,*) k, num
    write(30,*) k, ana
end do

编译（使用gfortran-8.2 + FFTW3.3.8 + OSX10.11）：

$ gfortran -fcheck=all -Wall sine.f90 -I/usr/local/Cellar/fftw/3.3.8/include -L/usr/local/Cellar/fftw/3.3.8/lib -lfftw3

如果我们像原始代码一样使用FFTW_FORWARD，我们会得到： 这个有一个负的叶片（其中fort.10、fort.20和fort.30对应于FFTW、积分和解析结果）。将代码修改为使用FFTW_RODFT00会改变结果如下，因此修改似乎是有效的（但请参见下面的网格定义）。 附加说明

• I have slightly modified the grid definition for r and k in my code (Lines (2-a) and (2-b)), which is found to improve the accuracy. But I'm still not sure whether the above definition matches the definition used by FFTW, so please read the manual for details...

• The fftw3.f03 header file gives the interface for fftw_plan_r2r_1d

  type(C_PTR) function fftw_plan_r2r_1d(n,in,out,kind,flags) bind(C, name='fftw_plan_r2r_1d')
    import
    integer(C_INT), value :: n
    real(C_DOUBLE), dimension(*), intent(out) :: in
    real(C_DOUBLE), dimension(*), intent(out) :: out
    integer(C_FFTW_R2R_KIND), value :: kind
    integer(C_INT), value :: flags
  end function fftw_plan_r2r_1d
  

• (Because of no Tex support, this part is very ugly...) The integral of 4 pi r^2 * exp(-r^2) * sin(kr)/(kr) for r = 0 -> infinite is pi^(3/2) * exp(-k^2 / 4) (obtained from Wolfram Alpha or by noting that this is actually a 3-D Fourier transform of exp(-(x^2 + y^2 + z^2)) by exp(-i*(k1 x + k2 y + k3 z)) with k =(k1,k2,k3)). So, although a bit counter-intuitive, the result becomes a positive Gaussian.

• I guess the r-grid can be chosen much coarser (e.g. delta up to 0.4), which gives almost the same accuracy as long as it covers the frequency domain of the transformed function (here exp(-r^2)).

- roygvib

---

这是正确的答案。我确实没有时间深入研究，但现在看到你的更改，确实是必要的。 - Vladimir F Героям слава

非常感谢@roygvib。我真的很感激你。你的回答是正确和完美的。 - Mohammed Alhissi

Answer 2

当然，有限高斯频谱的FFT的实部存在负成分。你只是使用了变换的实部。因此，你的绘图是绝对正确的。

你似乎将实部误认为是幅度，幅度当然不会是负数。要计算幅度，你需要使用 fftw_plan_dft_r2c_1d 并计算复系数的绝对值。或者你可能将傅里叶变换误认为是有限DFT。

你可以在这里检查以确保你上面的计算是正确的：

http://docs.mantidproject.org/nightly/algorithms/FFT-v1.html

请注意，上面页面上的图形已经被移动，使得频率为0的点在频谱的中间。

引用自己的话，对于所有k>1的情况下，数值积分[r*exp(-(r^2))*sin(kr)]dr如果最高频率归一化为0，则会有负分量。

简而言之，您的绘图是绝对先进的，与离散和有限的函数分析一致。

- Kaveh Vahedipour