困惑：N个人坐在圆桌周围。不交叉握手的方式数量。

Question

我们有n个人坐在圆桌旁边。任意两个人可以握手。这n个人如何进行握手，以使得没有两次握手相交？

我在技术面试论坛中发现了这个谜题，但是没有答案。我能想到的一种方法是找到所有握手的排列，然后检查每个排列是否满足要求。

请问有没有更有效率的解决方案？

@编辑：从评论中澄清：N必须是偶数。

- user2328404

---

我假设握手必须同时发生。所以如果有4个人坐在桌子周围，第1个人可以与他左边的人握手，这时另外2个人也可以同时握手。这是1种组合。然后第2个人可以与对面的人握手，但这不允许其他两个人握手。这是2种组合。然后他可以与右边的人握手，这样其他两个人也可以握手。总共有3种组合。这是对问题的正确理解吗？ - Lasse V. Karlsen

然后，如果桌子周围有5个人，一旦第一个握手将桌子分成了3个“在一起”的人，那么在这个小组中我们又有多种组合方式？ - Lasse V. Karlsen

当 n 为偶数时，解由卡特兰数C(n/2)给出（当 n 为奇数时解为0）。参见[OEIS A000108]（http://oeis.org/A000108）：“在圆上连接2n个点以形成n条不相交弦的方法数”。 - nneonneo

@LasseV.Karlsen 是的，你说得完全正确。 - user2328404

Answer 1

我会尝试一种分治解决方案。如果人1与人x握手，则剩下的人可以分成两组，可以视为坐在两个圆桌上。

- Buhb

---

这可以通过记忆化非常高效地实现，只需要进行 n 次查找（以及计算值直到 n）。 - nneonneo

每个子组必须包含偶数人或零人。棘手的部分是高效地找到重复的解决方案。 - Skizz

@Skizz：没有重复的解决方案！如果你总是将第一个人与另一个人配对，很容易看出不会有重复。 - nneonneo

@nneonneo：如果你有10个人（P1-P10），并且进行了顶层划分P1-P2、P1-P4、P1-P6等，然后进行了顶层划分P2-P3、P2-P5等，那么当你到达P3作为分割者时，P3-P1与已经完成的P1-P3相同。 - Skizz

不，我不明白。你能举个例子说明哪些握手配对会被计算两次吗？ - nneonneo

Answer 2

这个解决方案非常简单，以 Python 函数的形式给出（Python 3.3+）：

@lru_cache(maxsize=None) # memoize
def num_handshakes(n):
    if n % 2 == 1: return 0
    elif n == 0: return 1
    res = 0
    for i in range(0, n, 2):
        res += num_handshakes(i) * num_handshakes(n-2-i)
    return res

例子：

>>> num_handshakes(8)
14

这基本上实现了@Buhb的分治方法。另一种解决方案是，一旦我们知道答案与卡塔兰数有关：

from math import factorial as fac
def catalan(n):
    return fac(2*n) // fac(n+1) // fac(n)

def num_handshakes(n):
    if n % 2 == 1: return 0
    return catalan(n//2)

- nneonneo

Answer 3

我会尝试使用分治解决方案。如果第1个人与第x个人握手，则其余的人分为两组，可以视为坐在两张圆桌旁。

@Buhb是正确的。这个递归关系是：

f(n) = sum( f(i-2) + f(n-i) for i in range(2, n))

或者在代码中

def f(n):
    if n == 0:
        # zero people can handshake
        return 1

    if n == 1:
        # it takes two to tango
        return 0

    ways = 0

    # what if person 1 shakes with person i ?
    for i in range(2, n+1):
        # splits table into independent sets 2 .. i-1 and i+1 .. n
        ways += f(i-2) * f(n-i)

    return ways

一个奇数人数的群体不能握手，但前几个偶数位置的f值分别为1、2、5、14、42。

在整数序列百科全书中搜索，这看起来像是著名的卡特兰数http://oeis.org/A000108

这些序列真的相同吗？还是只是起始相似？它们是相同的。一本数学书证实了我们定义f的递归关系也适用于卡特兰数 https://en.wikipedia.org/wiki/Catalan_number#Properties。

- Colonel Panic

---

请问您能否解释一下为什么我们要将左子表和右子表的计数相乘？我认为将它们相加更有意义，而不是相乘。 - Syed

Answer 4

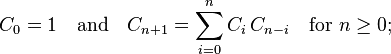
回溯算法怎么样？

1. 从一个握手开始，查找仍然可能的握手。如果不再有“非交叉”握手，则进行回溯。继续回溯，直到没有更多的搜索树分支可以通过“非交叉”握手扩展。
2. 结果搜索树的所有顶点都是“非交叉”的握手。

由于您的桌子是圆形（对称），因此您可以通过假设人员0始终是最上面的握手之一来优化问题。

- MrSmith42

Answer 5

我认为这可能是一个解决方案，即使 n=2m.

将人们从1到2m编号。

在第 j 轮中，1≤j≤m，人员 j 与人员 j+1 握手，所有其他握手都“平行”于此（因此，j-1 与 j+2，j-2 与 j+3 等等 - 在整个过程中，必要时标签按模数解释）。在这 m 轮结束时，每个人都与所有离他们奇数距离的人握过手。

在第 m+j 轮中，1≤j≤m，j 与 j+2 握手，所有其他握手都是平行的（因此 j-1 与 j+3，j-2 与 j+4 等等）。这处理了所有相隔偶数人的情况。因此总共需要 2m 轮。

如问题陈述中所述，2m-1 轮是不可能的，因此答案是 2m。

奇数情况更容易。在第 j 轮中，人员 j 不参与，而 j-1 与 j+1 打招呼，j-2 与 j+2 打招呼，以此类推，同样使用 n 轮。

- Padmanathan J

Answer 6

这里的结果遵循卡特兰数列。以下是我的C++代码：

#include <bits/stdc++.h>
using namespace std;
long c[17] ;
void sieve(){
    c[0] = 1;
    c[1] = 1;
    for(int i =2;i<=15;i++){
        for(int j =0;j<i;j++){
            c[i] += c[j]*c[i-j-1];
        }
    }
}

int main(void){
    sieve();
    int t;
    scanf("%d",&t);
    while(t--){
        int n ;
        scanf("%d",&n);
        if(n%2!=0){
            cout<<"0"<<endl;
        }
        else{
            n = n>>1;
            cout<<c[n]<<endl;
        }
    }

    return 0;
}

- HeadAndTail

Answer 7

由于有n个人且每次只有2个人握手，如果假设A与B握手，B又与A握手，我们不能重复计算即AB和BA都不能被计算，这意味着排列不成立，即不是排列而是组合问题...

因此，应用组合公式变为：nC2 => (n*(n-1))/2。

因此，我们可以直接将此公式应用于问题以得到答案。

- Manish Khandelwal

---

这不是正确的答案。例如，当N = 8时，答案是14。但组合公式给出的是28。 - Syed

Answer 8

人们可以用 (n-1)+(n-2)+.....+1 种方式进行握手。这是针对线性的。

圆桌有 n 种方式。

- DRAJI

---

那么在桌子周围有4个人的情况下，有多少种可能的有效组合？ - Lasse V. Karlsen

3+2+1=6。所以4个人有6种方式。 - DRAJI

@DRAJI：不是6，而是2。记住握手不能交叉。因此，唯一两个有效的选项是：A与左边的人握手，其他两个人握手；或者A与右边的人握手，其他两个人握手。A不能与对面的人握手，因为另外两个人需要交叉。选择另一个人作为A只会复制已经找到的两个解决方案。 - Skizz

@DRAJI：在桌子周围有4个人的情况下，是的，只有另外两个人是有效的，第三个人由于交叉而无效。 - Skizz

好的。最终我们为4个人准备了4份奶昔。这意味着对于n个人，有n种可能的方式。@Skizz - DRAJI