让我们逐步尝试编写自己的函数来解决问题中指定的WBM问题。
使用pulp,当我们有两组节点(u和v,边权重和顶点容量)时,很容易制定和解决加权二分匹配(WBM)问题。
在下面的第2步中,您将找到一个(希望易于理解)的函数,将WBM制定为ILP并使用pulp求解。仔细阅读它,看看它是否有所帮助。(您需要pip安装pulp)
步骤1:设置二分图容量和边权重
import networkx as nx
from pulp import *
import matplotlib.pyplot as plt
from_nodes = [1, 2, 3]
to_nodes = [1, 2, 3, 4]
ucap = {1: 1, 2: 2, 3: 2}
vcap = {1: 1, 2: 1, 3: 1, 4: 1}
wts = {(1, 1): 0.5, (1, 3): 0.3,
(2, 1): 0.4, (2, 4): 0.1,
(3, 2): 0.7, (3, 4): 0.2}
def create_wt_doubledict(from_nodes, to_nodes):
wt = {}
for u in from_nodes:
wt[u] = {}
for v in to_nodes:
wt[u][v] = 0
for k,val in wts.items():
u,v = k[0], k[1]
wt[u][v] = val
return(wt)
步骤2:解决WBM问题(将其制定为整数规划)
以下是一些描述,以使接下来的代码更容易理解:
- WBM是任务分配问题的变体。
- 我们将右侧节点与左侧节点进行“匹配”。
- 边具有权重。
- 目标是最大化所选边的权重之和。
- 额外一组约束条件:对于每个节点,选择的边数必须小于其指定的“容量”。
- 如果您不熟悉
puLP,请参考PuLP文档。
.
def solve_wbm(from_nodes, to_nodes, wt):
''' A wrapper function that uses pulp to formulate and solve a WBM'''
prob = LpProblem("WBM Problem", LpMaximize)
choices = LpVariable.dicts("e",(from_nodes, to_nodes), 0, 1, LpInteger)
prob += lpSum([wt[u][v] * choices[u][v]
for u in from_nodes
for v in to_nodes]), "Total weights of selected edges"
for u in from_nodes:
for v in to_nodes:
prob += lpSum([choices[u][v] for v in to_nodes]) <= ucap[u], ""
prob += lpSum([choices[u][v] for u in from_nodes]) <= vcap[v], ""
prob.writeLP("WBM.lp")
prob.solve()
print( "Status:", LpStatus[prob.status])
return(prob)
def print_solution(prob):
for v in prob.variables():
if v.varValue > 1e-3:
print(f'{v.name} = {v.varValue}')
print(f"Sum of wts of selected edges = {round(value(prob.objective), 4)}")
def get_selected_edges(prob):
selected_from = [v.name.split("_")[1] for v in prob.variables() if v.value() > 1e-3]
selected_to = [v.name.split("_")[2] for v in prob.variables() if v.value() > 1e-3]
selected_edges = []
for su, sv in list(zip(selected_from, selected_to)):
selected_edges.append((su, sv))
return(selected_edges)
第三步:指定图表并调用WBM求解器。
wt = create_wt_doubledict(from_nodes, to_nodes)
p = solve_wbm(from_nodes, to_nodes, wt)
print_solution(p)
这将会给出:
Status: Optimal
e_1_3 = 1.0
e_2_1 = 1.0
e_3_2 = 1.0
e_3_4 = 1.0
Sum of wts of selected edges = 1.6
第四步:可选地使用Networkx绘制图形。
selected_edges = get_selected_edges(p)
graph = nx.Graph()
colors = []
for u in from_nodes:
for v in to_nodes:
edgecolor = 'blue' if (str(u), str(v)) in selected_edges else 'gray'
if wt[u][v] > 0:
graph.add_edge('u_'+ str(u), 'v_' + str(v))
colors.append(edgecolor)
def get_bipartite_positions(graph):
pos = {}
for i, n in enumerate(graph.nodes()):
x = 0 if 'u' in n else 1
pos[n] = (x,i)
return(pos)
pos = get_bipartite_positions(graph)
nx.draw_networkx(graph, pos, with_labels=True, edge_color=colors,
font_size=20, alpha=0.5, width=3)
plt.axis('off')
plt.show()
print("done")
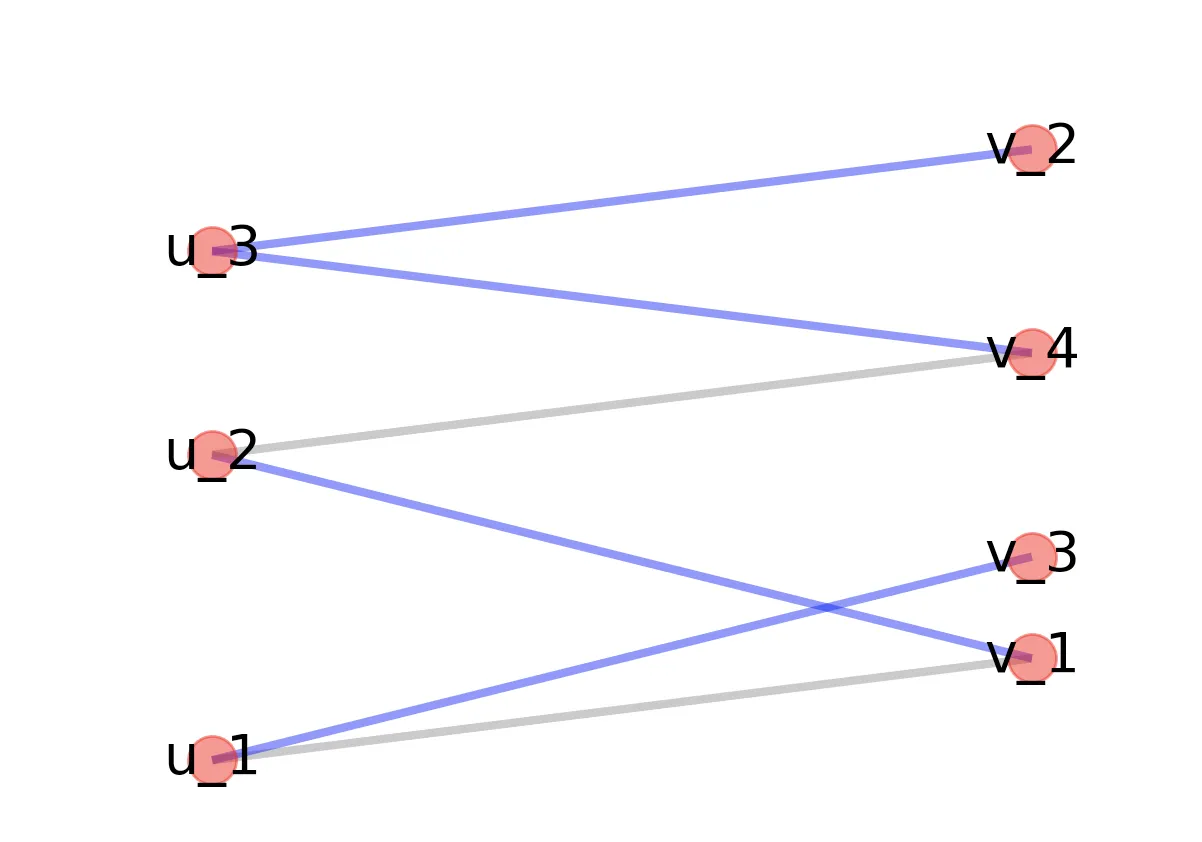
蓝色的边缘是被选为WBM的边缘。希望这可以帮助您继续前进。
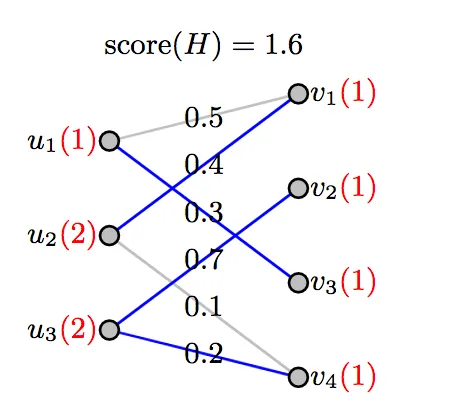

b表示可以连接到该顶点的边的数量。 我们可以说MWM是WBM的一个特例,其中每个顶点的容量为1。 使用顶点的容量对问题进行建模有助于解决一对多问题,例如一个评审人具有审阅b篇文章的能力。 - Sina