logo标签列表

在一个大圆内放置N个不同半径的小圆，且不允许重叠。

algorithmlanguage-agnosticgeometry
32
给定n个半径为r1 ... rn的圆，将它们放置在不重叠的情况下，并使外围圆的半径尽可能“小”。
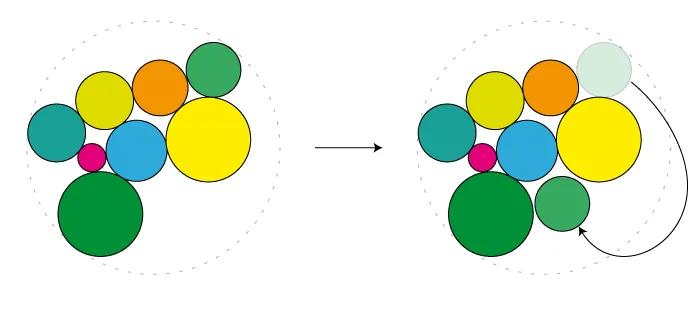
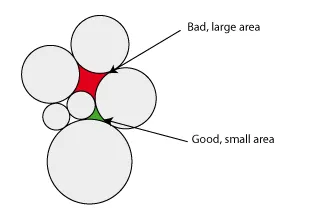
该程序以列表[r1，r2，... rn]作为输入，并输出圆的中心。
我之所以要求“小”，是因为“最小”半径会将其转换为一个更加困难的问题（最小版本已被证明是NP难/完全的 - 请参见问题末尾的脚注）。我们不需要最小值。如果圆形成的形状似乎相当圆形，那就足够了。
如果有帮助，您可以假设Rmax / Rmin <20。
低优先级的问题 - 程序应能处理2000多个圆。作为起点，即使100-200个圆也应该没问题。
您可能已经猜到，圆形不需要紧密地堆放在一起甚至不接触。
目标是设计一个视觉上令人愉悦的圆形排列方式，这些圆可以放入一个更大的圆中，并且不会留下太多空白空间（就像色盲测试图片中的圆形一样）。 alt text 您可以使用以下Python代码作为起点（在Linux上需要numpy和matplotlib -“sudo apt-get install numpy matplotlib”）...
import pylab
from matplotlib.patches import Circle
from random import gauss, randint
from colorsys import hsv_to_rgb

def plotCircles(circles):
    # input is list of circles
    # each circle is a tuple of the form (x, y, r)
    ax = pylab.figure()
    bx = pylab.gca()
    rs = [x[2] for x in circles]
    maxr = max(rs)
    minr = min(rs)
    hue = lambda inc: pow(float(inc - minr)/(1.02*(maxr - minr)), 3)

    for circle in circles:
        circ = Circle((circle[0], circle[1]), circle[2])
        color = hsv_to_rgb(hue(circle[2]), 1, 1)
        circ.set_color(color)
        circ.set_edgecolor(color)
        bx.add_patch(circ)
    pylab.axis('scaled')
    pylab.show()

def positionCircles(rn):
    # You need rewrite this function
    # As of now, this is a dummy function
    # which positions the circles randomly
    maxr = int(max(rn)/2)
    numc = len(rn)
    scale = int(pow(numc, 0.5))
    maxr = scale*maxr

    circles = [(randint(-maxr, maxr), randint(-maxr, maxr), r)
               for r in rn]
    return circles

if __name__ == '__main__':
    minrad, maxrad = (3, 5)
    numCircles = 400

    rn = [((maxrad-minrad)*gauss(0,1) + minrad) for x in range(numCircles)]

    circles = positionCircles(rn)
    plotCircles(circles)

补充信息：在谷歌搜索结果中常被称为“圆形装配算法”的算法不适用于此问题。

另一个“圆形装配算法”的问题陈述如下：给定一个复合K（在这个上下文中称为单纯复合或简称为复合）和适当的边界条件，计算K对应圆形装配的半径...

它基本上从一个图形开始，说明哪些圆相互接触（图形的顶点表示圆，边表示圆之间的接触/切线关系）。必须找到圆的半径和位置，以满足图形所表示的接触关系。

另一个问题确实有一个有趣的观察结果（与此问题无关）：

圆形装配定理 - 每个圆形装配都有一个对应的平面图（这是易于理解的部分），每个平面图都有一个对应的圆形装配（这是不太明显的部分）。图形和装配是彼此的对偶，并且是唯一的。

我们没有一个平面图或切线关系来开始解决我们的问题。

这篇文章 - 罗伯特·J·福勒，迈克·帕特森，史蒂文·L·塔尼莫托：平面上的最优装箱和覆盖问题是NP完全问题 - 证明了此问题的最小版本是NP完全问题。然而，该论文不易在网上获取。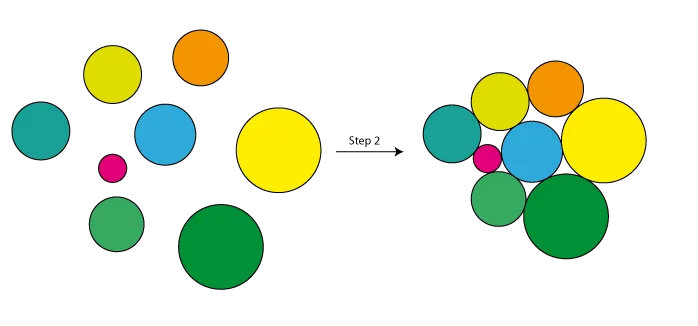
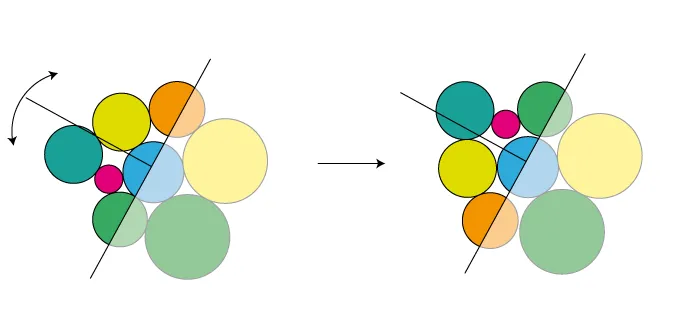不是谜题...这是我在工作中一直苦苦挣扎的问题。我有一个基本的解决方案，但我正在寻找更好的解决方案。 - Rajan
2
在你的评论后，我再次检查了我的问题，但没有看到谜题部分。请告诉我，如果问题的形式表明它是一个非常严肃的谜题类型的问题，我会重新表述它。或者，你是说这个问题对于Stack Overflow来说太难了吗？ - Rajan
2
@Greg Hewgill：他正在寻找一个NP难问题的近似解。如果不是在编程/计算机科学问答网站上，他还能去哪里问呢？ - Niki
@nikie：我的观点是我不反对这种问题。我只是在告诉其他 Stack Overflow 上的人的想法。 - user238469
@Loic - 是的，在发布问题之前我完成了我的功课（实际上在提出启发式方法之前我进行了很多研究）。http://www.google.com/search?hl=en&q=packing+unequal+circles+in+a+circle&btnG=Search&aq=f&aqi=&aql=&oq=&gs_rfai= 用于在圆中装填不等圆的结果。 - Rajan
显示剩余9条评论
5个回答
19

不是一种解决方案，仅仅是一个头脑风暴的想法：据我所知，求解TSP问题的一种常见方法是从随机构造开始，然后通过应用局部操作（例如在路径中“交换”两个边）来尝试得到越来越短的路径。（维基百科链接）

我认为在这里也可能有类似的方法：

  1. 从随机位置开始
  2. “优化”这些位置，使圆没有重叠且尽可能靠近，通过增加重叠的圆之间的距离和减小其他圆之间的距离，直到它们密集地排列。这可以通过某种能量最小化来完成，或者可能存在更有效的贪婪算法。alt text
  3. 对中心位置应用迭代改进运算符
  4. 回到步骤2，在达到最大迭代次数或者上一次迭代没有发现任何改进后退出

有趣的问题是：在步骤3中，你可以使用什么样的“迭代改进运算符”？我们可以假设此阶段的位置是局部最佳的，但它们可能通过重新排列大部分圆来改善。我的建议是任意选择一条穿过圆形的线路。然后选取所有在该线路“左侧”的圆，并在与该线路垂直的某个轴上对其进行镜像反射： alt text 你可能会尝试多条线路并选择导致解决方案最紧凑的线路。

这个想法是，如果某些圆已经处于或接近其最佳配置，则有很大的机会这个操作不会扰乱它们。

我能想到的其他可能的操作：

  • 取距离中心最远的一个圆（与边界圆相切的圆之一），将其随机移动到其他位置： alt text
  • 选择一组彼此靠近的圆（例如，它们的中心位于一个随机选择的圆内），并将其旋转一个随机角度。
  • 另一个选项（尽管有点更加复杂）是在圆紧密堆叠时测量它们之间的面积:

    • alt text

    然后你可以选择与最大圆间面积相邻的一个圆，并将其与另一个圆交换位置，或将其移动到边界上的某个位置。

    （回复评论：）请注意，这些“改进”几乎肯定会创建重叠和/或不必要的空间。但在下一次迭代中，步骤2将移动圆形，使它们再次紧密堆叠并且不重叠。这样，我就可以有一个用于局部优化的步骤（不关心全局优化），以及一个用于全局优化的步骤（可能会创建局部次优解）。这比有一个既做局部又做全局优化的复杂步骤要容易得多。

    线镜像是一个不错的想法，可以在不破坏本地优化的情况下进行全局更改，但当然也可能会创建重叠。 - Chris Johnson
    这里有一些很棒的想法，nikie...我会尝试将它们（如果可能的话）与rafe的方法结合起来，看看会有什么结果。 - Rajan
    15

    我有一个相当简单的（对于半径而言）一次通过的解决方案，可以产生不错的结果，虽然肯定还有改进的空间。我确实有一些这方面的想法，但我想也分享一下我现在的思路，以防其他人也想研究它。

    alt text

    看起来它们在中心相交，但事实并非如此。我用一个嵌套循环装饰了放置函数，该函数检查每个圆是否与每个其他圆相交（两次），如果有，则引发AssertionError异常。

    而且，通过简单地将列表反向排序，我可以使边缘接近完美，但我认为这种方式的中心看起来不太好。这是代码注释中（几乎是唯一的 ;)）讨论的内容。

    我的想法是只查看圆可能存在的离散点，并使用以下生成器迭代它们：

    def base_points(radial_res, angular_res):
    circle_angle = 2 * math.pi
    r = 0
    while 1:
        theta = 0
        while theta <= circle_angle:
            yield (r * math.cos(theta), r * math.sin(theta))
            r_ = math.sqrt(r) if r > 1 else 1
            theta += angular_res/r_
        r += radial_res

    这个算法从原点开始，按照同心圆的轨迹依次遍历各个点。我们按照某些参数对半径进行排序，使大圆靠近中心（列表开头），但足够多的小圆靠近开头填充空间。然后我们遍历半径，在主循环内部，首先循环查找并保存我们已经查看过的点。如果没有合适的点，我们就开始从生成器中抽取新的点并按顺序保存，直到找到一个合适的位置。然后放置圆形，并通过我们保存的点列表提取所有落在新圆内的点。我们接着重复这个过程，处理下一个半径。

    我会尝试一些想法，并让它变得更好。这可能是一个基于物理的好起点，因为你可以从没有重叠的情况开始。当然，它可能已经足够紧凑了，以至于你没有太多的空间。

    此外，我从未使用过numpy或matplotlib，所以我只用纯Python编写。也许有些东西可以让它运行得更快，我需要再看看。

    这看起来很棒。它让我想起了埃舍尔的双曲圆盘，因为大圆圈集中在中心附近。如果需要，我猜这可以改变而不会对算法产生太大影响(我还在努力理解你的算法，所以可能是错的)。此外，我仅使用numpy和matplotlib绘制图片。它们在我的存根中不进行任何处理。 - Rajan
    我很好奇...你的图片里有多少个圆？生成这个输出需要多长时间？ - Rajan
    @Rajan，这张图片里有400个圆。在我的机器上需要几分钟，但我的机器很慢，所以你可能不必等太久。不幸的是，它不适合用于实时的网络服务。要运行它，只需将链接中的代码复制并粘贴到您提供的存根函数上即可。 - aaronasterling
    @Rajan，整个代码可以在我帖子第一段中的链接http://pastebin.com/VciE4Js7中找到。它大约有124行，所以我不想把它放在这里。请注意，它还没有完全调试好，我仍然处于“让它工作”的阶段;) 它应该可以作为一个独立的模块导出positionCircles函数，或者只是粘贴到您提供的存根函数上。 - aaronasterling
    @aaronasterling：这太棒了！非常感谢！我还有一个问题想请教您：您如何设置大圆的半径并填充尽可能多的不重叠的小圆？也就是说，将大圆的直径作为主要参数，而不是选择小圆的数量？我一直在尝试调整您的代码来实现这一点，但由于大圆的半径从未起到作用，所以我一直遇到麻烦。 - Cynthia GS
    7

    你可以将圆视为带电粒子，放置在一个带电腔体内，并寻找稳定的解决方案。也就是说，圆形根据距离相互排斥，但向原点靠近时会相互吸引。进行几步模拟可能会得到一个不错的答案。

    2
    这对我来说听起来很有前途，特别是当它与某种退火时间表（http://en.wikipedia.org/wiki/Simulated_annealing）相结合时，该时间表在模拟早期引入随机噪声以混合粒子，并且（继续电荷类比）在模拟后期将势能调整得几乎成为方阱，以更准确地强制执行无穿透和全局圆形约束。 - Chris Johnson
    1
    这个答案是一种“能量最小化”的类型，可以作为nikie答案的第二步使用。 - Chris Johnson
    @Chris Johnson：没错。我想象每个圆都会被吸引到中心，两个圆一旦开始重叠就会互相排斥。但我猜结果可能差不多。 - Niki
    2
    2
    在谷歌搜索结果中常被提及的圆装箱算法并不适用于这个问题。该算法从一个平面图开始，推导出相应的“圆装箱”。这是根据瑟斯顿的“圆装箱定理”应用而来的。然而，我们没有一个平面图作为起点。如果我们有了平面图，找到圆装箱就可以在多项式时间内完成。这个问题在其一般形式上是NP完全的。 - Rajan
    另一个“圆装箱算法”的问题陈述如下：给定一个复杂的K（图K）和适当的边界条件，计算K的相应圆装箱的半径... 它基本上从一个图开始，告诉我们哪些圆形彼此接触（图的顶点表示圆形，边表示圆形之间的接触）。但是顶点和边在空间中是任意放置的。必须找到圆的半径和位置，以满足图所表示的接触关系。这与我们的问题不同。 - Rajan
    1
    我不确定如何使用垫片，但它们很漂亮。感谢您的发布。 - Rajan
    我认为这在特定的输入情况下可以工作：从三个最大的曲率/半径输入生成阿波罗尼亚垫，然后注意随后生成的曲率/半径。如果其余提供的半径对应于小于或等于生成的半径的半径，则可以简单地在预期在垫子中找到生成的圆的同心圆上绘制圆。但这不是一个非常好的解决方案，但它可能提供一些额外的见解。 - q__
    网页内容由stack overflow 提供, 点击上面的
    可以查看英文原文，
    原文链接