logo标签列表

帮我理解二元支持向量机中的线性可分性。

algorithmmachine-learningclassificationsvmlibsvm
5

我从math.stackexchange.com转发这篇文章，因为我没有得到任何反馈，而且对我来说这是一个时间紧迫的问题。

我的问题涉及支持向量机中的超平面线性可分性。
根据维基百科：
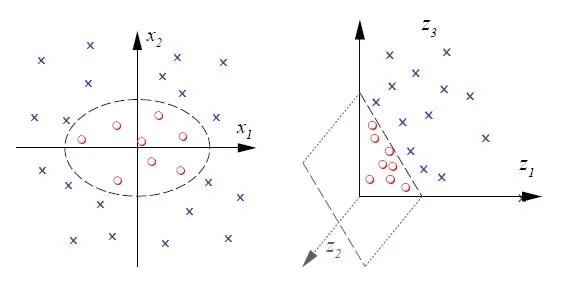
正式地说，支持向量机在高维或无限维空间中构建一个超平面或一组超平面，可用于分类、回归或其他任务。直观地说，通过具有任何类别的最近训练数据点（所谓的函数间隔）的距离最大的超平面来实现良好的分离，因为通常情况下，边界越大，分类器的泛化误差就越低。

对我来说，通过超平面进行类别的线性分离是有直观意义的。我认为我理解了二维几何中的线性可分性。然而，我正在使用一种流行的SVM库（libSVM）实现SVM时，当我玩弄数字时，我无法理解SVM如何在类别之间创建曲线，或者如何在n维空间V中，如果一个超平面是维数为n-1的“平坦”子集，或者在二维空间中 - 是一条1D线，则可以围绕类别1中心点内部的圆形曲线中包含被类别2包围的点。

这就是我的意思：

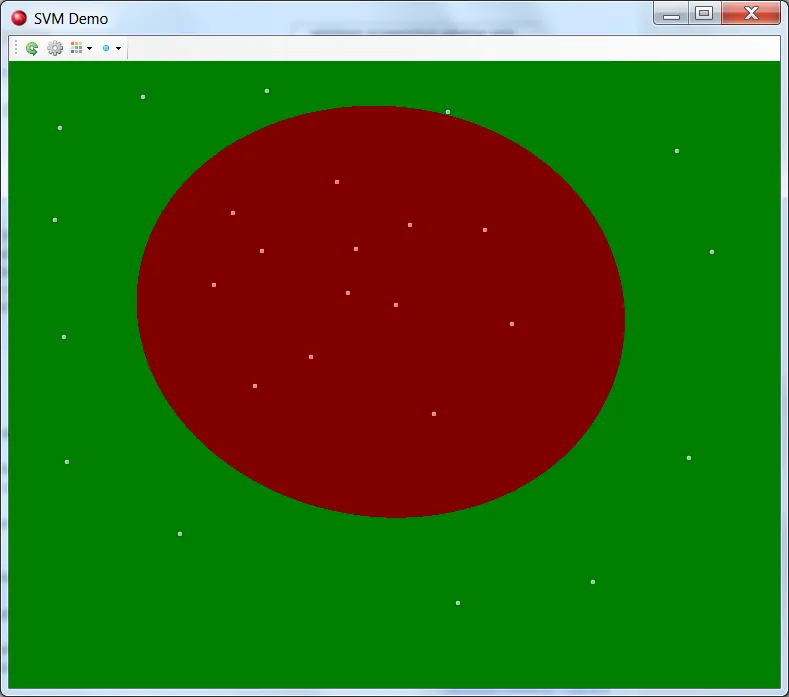
circularly enclosed class separation for a 2D binary SVM

那不是一个超平面，而是圆形的。这是怎么工作的？或者SVM里面有比二维输入特征更多的维度吗？

这个示例应用程序可以从这里下载。

编辑：

感谢您详尽的回答。因此，SVM可以通过使用核函数很好地分离奇怪的数据。在将数据发送到SVM之前，将其线性化是否有帮助？例如，我的一个输入特征（数值）具有拐点（例如0），在该拐点处它完美地适合于类别1，但在零以上和以下，则适合于类别2。现在，因为我知道这一点，将该特征的绝对值发送给SVM是否有助于分类？

2
线性化数据是一种选择，但核函数的一个好处是你实际上不需要构建这样的空间。核函数有效地衡量了数据点之间的不相似度。实际上，找到一个能够实现任意内积的空间可能涉及引入无限多个维度。但是，SVM算法所需的只是一个内积。事实上，如果我没记错的话，它所需要的只是足够“像”内积的东西。 - mokus
这个问题在这里是相关的：http://stats.stackexchange.com/ - Shane
1
@Shane：是的，但是SO拥有更大的受众群体，可以更快地得到答案。 - Petrus Theron
7个回答
12

正如mokus所解释的，支持向量机使用一个核函数来将数据隐式映射到一个特征空间中，在这个空间中它们是线性可分的:

SVM mapping one feature space into another

不同的核函数用于各种各样的数据。请注意，图片中的变换会增加一个额外的维度（特征），虽然这个特征在内存中从未实现。

（图片来源：Chris Thornton, U. Sussex。）

SVM如何知道哪个核函数能够合理地分离数据？它是否遍历一堆方程，并计算哪一个产生最大的间隔？请参阅我问题的编辑。 - Petrus Theron
1
内核通常由用户/开发者作为参数设置。例如，LibSVM具有线性、多项式、RBF和Sigmoid内核类型。其作者建议初学者使用RBF内核。 - Fred Foo
9

请查看这个YouTube视频，它展示了一个线性不可分点的例子，当它们映射到更高维度时，可以通过一个平面进行分离。

alt text

很棒的视频，我希望能找到更多类似的东西！ - Diego
3
我不太熟悉支持向量机(SVM)，但从我学习的内容中记得，它们通常与“核函数”一起使用——本质上是标准内积的替代品，可以有效地非线性化空间。这相当于将非线性变换应用于您的空间，使其转换为某个“工作空间”，在该空间中应用线性分类器，然后将结果拉回到原始空间，其中分类器处理的线性子空间不再是线性的。
维基百科文章在“非线性分类”小节中提到了这一点，并链接到http://en.wikipedia.org/wiki/Kernel_trick，更详细地解释了这种技术。
据我记得，Numerical Recipes 中有一个非常好的章节，介绍了使用核函数实现 SVM 以解决非线性分类问题。 - mokus
实际上，“将结果拉回”步骤是不必要的，即使您手动进行特征空间扩展。您只需在扩展的特征空间中执行点积，为每个支持向量/测试样本对提供一个单一数字。 - Fred Foo
2
这是通过应用所谓的[核技巧]（Kernel Trick）来实现的(http://en.wikipedia.org/wiki/Kernel_trick)。基本上，如果某些东西在现有输入空间中不是线性可分的（在您的情况下是2-D），则会将其投影到更高的维度，使其可分。核函数（可以是非线性的）被应用于修改您的特征空间。然后在此特征空间中执行所有计算（该空间可能也是无限维的）。
使用此核函数转换了输入中的每个点，并且所有进一步的计算都是按照这是您原始输入空间的方式进行的。因此，您的点可能在更高的维度（可能是无限的）中是可分离的，因此更高维度中的线性超平面在原始维度中可能不是线性的。
以XOR的简单示例为例。如果您将Input1绘制在X轴上，将Input2绘制在Y轴上，则输出类将为：
1.第0类：(0,0)，(1,1) 2.第1类：(0,1)，(1,0)
正如您所观察到的那样，它在2-D中不是线性可分的。但是，如果我将这些有序对移动到3-D中（只需在3-D中移动1个点），例如：
1.第0类：(0,0,1)，(1,1,0) 2.第1类：(0,1,0)，(1,0,0)
现在，您可以轻松观察到3-D中有一个平面可用于线性分离这两个类。
因此，如果将输入投影到足够大的维度（可能是无限的），则您将能够在线性方面分离您的类。
这里需要注意的一个重要点（也许我还会回答您的另一个问题）是，您不必自己制作核函数（就像我上面制作的那样）。好处在于，核函数自动处理您的输入并找出如何“线性化”它。
1

对于在二维空间中给出的SVM示例，假设x1和x2是两个轴。您可以有一个转换函数F = x1^2 + x2^2，并将此问题转换为一维空间问题。如果您仔细观察，您会发现在转换后的空间中，您可以轻松地线性分离点（在F轴上的阈值）。这里转换后的空间是[ F ]（1维）。在大多数情况下，您将增加维度以获得线性可分的超平面。

这也是我的理解，因为它是基于核函数输出的线性而不是核函数本身形状的。如果有四个维度F=x1^2 + x2^2 + x3^3 + x4^2，它在F值的阈值上仍然是一维的。 - Vass
0
0

我之前回答的问题可能会让你对这种情况发生的原因有一些了解。我给出的例子非常人为，不是在SVM中真正发生的情况，但它应该能给你一些直观的印象。

网页内容由stack overflow 提供, 点击上面的
可以查看英文原文，
原文链接