为了开始,您需要做一些假设。
1. n相对于任何常数项都很大。
2. 您可以有效地随机输入数据。
3. 您可以采样足够密集的数据以更好地了解运行时间的分布情况。
特别地,(3)很难与(1)共同实现。因此,您可能会得到一个最坏情况下呈指数增长的算法,但从未遇到过该最坏情况,因此认为您的算法平均而言比它实际上好得多。
说了这么多,您只需要任何标准曲线拟合库。
Apache Commons Math有一个完全足够的库。然后,您可以创建一个包含您想要测试的所有常见术语的函数(例如:常数、log n、n、n log n、n
n、nn*n、e^n),或者取对数并拟合指数,然后如果您得到的指数不接近整数,请看看是否加入log n可以获得更好的拟合结果。
更详细地说,如果你适合使用
C*x^a 表示
C 和
a,或者更容易的是
log C + a log x,你就可以得到指数
a;在一次性处理所有常见项的方案中,你将获得每个项的权重,因此如果你有
n*n + C*n*log(n),其中
C 很大,你也会捕捉到该项。
你需要足够变化大小,以便你可以区分不同的情况(如果你关心对数项可能会很难),并且安全地比你有的参数更多的不同大小(可能 3 倍的过剩会开始变得可行,只要你总共运行至少十几次)。
编辑:这里有一份Scala代码,可以为您完成所有操作。我不会解释每个小部分,而是让你自己去探索它; 它使用C * x ^ a拟合实现了上面的方案,并返回((a,C),(a的下限,a的上限))。由于您可以从运行几次中看到,这些边界非常保守。 C 的单位为秒(a 无单位),但不要太相信它,因为有一些循环开销(还有一些噪音)。
class TimeLord[A: ClassManifest,B: ClassManifest](setup: Int => A, static: Boolean = true)(run: A => B) {
@annotation.tailrec final def exceed(time: Double, size: Int, step: Int => Int = _*2, first: Int = 1): (Int,Double) = {
var i = 0
val elapsed = 1e-9 * {
if (static) {
val a = setup(size)
var b: B = null.asInstanceOf[B]
val t0 = System.nanoTime
var i = 0
while (i < first) {
b = run(a)
i += 1
}
System.nanoTime - t0
}
else {
val starts = if (static) { val a = setup(size); Array.fill(first)(a) } else Array.fill(first)(setup(size))
val answers = new Array[B](first)
val t0 = System.nanoTime
var i = 0
while (i < first) {
answers(i) = run(starts(i))
i += 1
}
System.nanoTime - t0
}
}
if (time > elapsed) {
val second = step(first)
if (second <= first) throw new IllegalArgumentException("Iteration size increase failed: %d to %d".format(first,second))
else exceed(time, size, step, second)
}
else (first, elapsed)
}
def multibench(smallest: Int, largest: Int, time: Double, n: Int, m: Int = 1) = {
if (m < 1 || n < 1 || largest < smallest || (n>1 && largest==smallest)) throw new IllegalArgumentException("Poor choice of sizes")
val frac = (largest.toDouble)/smallest
(0 until n).map(x => (smallest*math.pow(frac,x/((n-1).toDouble))).toInt).map{ i =>
val (k,dt) = exceed(time,i)
if (m==1) i -> Array(dt/k) else {
i -> ( (dt/k) +: (1 until m).map(_ => exceed(time,i,first=k)).map{ case (j,dt2) => dt2/j }.toArray )
}
}.foldLeft(Vector[(Int,Array[Double])]()){ (acc,x) =>
if (acc.length==0 || acc.last._1 != x._1) acc :+ x
else acc.dropRight(1) :+ (x._1, acc.last._2 ++ x._2)
}
}
def alpha(data: Seq[(Int,Array[Double])]) = {
val dat = data.map{ case (i,ad) => math.log(i) -> ad.map(x => math.log(i) -> math.log(x)) }
val slopes = (for {
i <- dat.indices
j <- ((i+1) until dat.length)
(pi,px) <- dat(i)._2
(qi,qx) <- dat(j)._2
} yield (qx - px)/(qi - pi)).sorted
val mbest = slopes(slopes.length/2)
val mp05 = slopes(slopes.length/20)
val mp95 = slopes(slopes.length-(1+slopes.length/20))
val intercepts = dat.flatMap{ case (i,a) => a.map{ case (li,lx) => lx - li*mbest } }.sorted
val bbest = intercepts(intercepts.length/2)
((mbest,math.exp(bbest)),(mp05,mp95))
}
}
请注意,
multibench方法预计需要大约sqrt(2)
nm*time的时间运行,假设使用静态初始化数据,并且与您正在运行的内容相比相对便宜。以下是一些参数选取为大约15秒运行时间的示例:
val tl1 = new TimeLord(x => List.range(0,x))(_.sum) // Should be linear
// Try list sizes 100 to 10000, with each run taking at least 0.1s;
// use 10 different sizes and 10 repeats of each size
scala> tl1.alpha( tl1.multibench(100,10000,0.1,10,10) )
res0: ((Double, Double), (Double, Double)) = ((1.0075537890632216,7.061397125245351E-9),(0.8763463348353099,1.102663784225697))
val longList = List.range(0,100000)
val tl2 = new TimeLord(x=>x)(longList.apply) // Again, should be linear
scala> tl2.alpha( tl2.multibench(100,10000,0.1,10,10) )
res1: ((Double, Double), (Double, Double)) = ((1.4534378213477026,1.1325696181862922E-10),(0.969955396265306,1.8294175293676322))
// 1.45?! That's not linear. Maybe the short ones are cached?
scala> tl2.alpha( tl2.multibench(9000,90000,0.1,100,1) )
res2: ((Double, Double), (Double, Double)) = ((0.9973235607566956,1.9214696731124573E-9),(0.9486294398193154,1.0365312207345019))
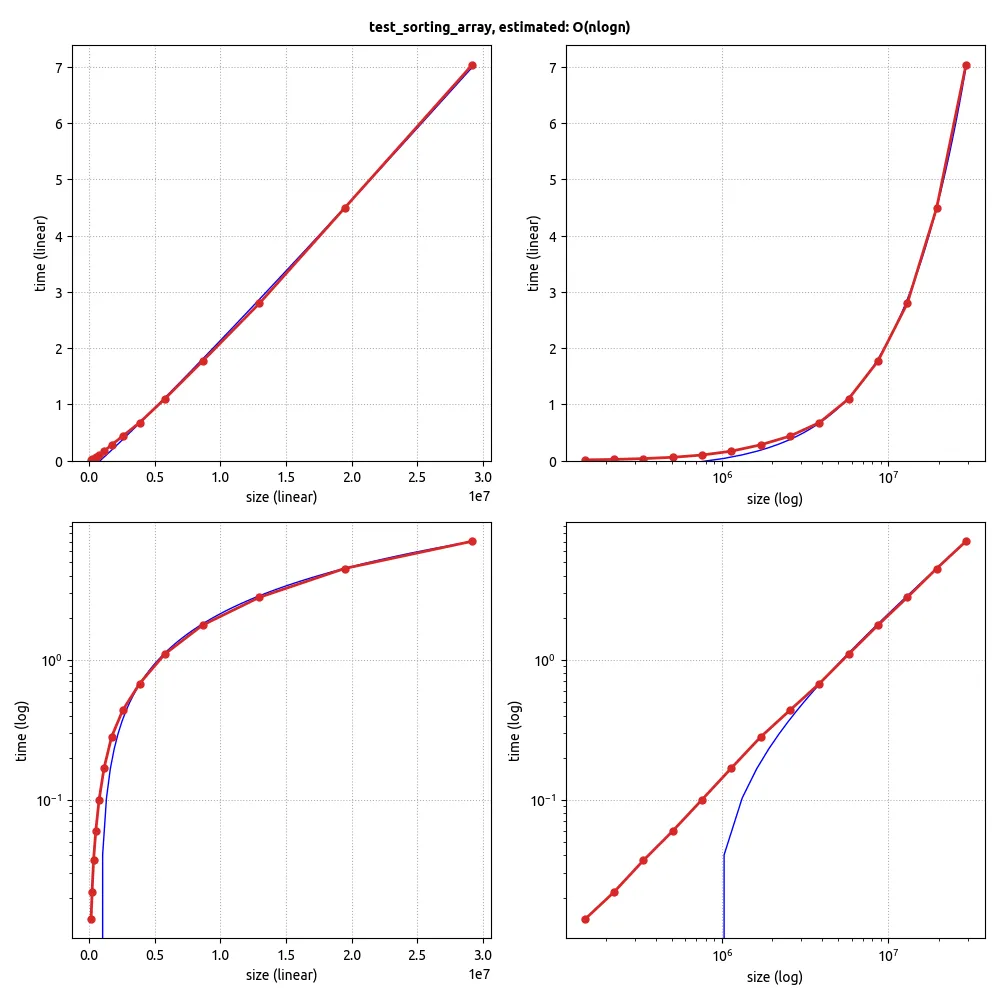
// Let's try some sorting
val tl3 = new TimeLord(x=>Vector.fill(x)(util.Random.nextInt))(_.sorted)
scala> tl3.alpha( tl3.multibench(100,10000,0.1,10,10) )
res3: ((Double, Double), (Double, Double)) = ((1.1713142886974603,3.882658025586512E-8),(1.0521099621639414,1.3392622111121666))
// Note the log(n) term comes out as a fractional power
// (which will decrease as the sizes increase)
// Maybe sort some arrays?
// This may take longer to run because we have to recreate the (mutable) array each time
val tl4 = new TimeLord(x=>Array.fill(x)(util.Random.nextInt), false)(java.util.Arrays.sort)
scala> tl4.alpha( tl4.multibench(100,10000,0.1,10,10) )
res4: ((Double, Double), (Double, Double)) = ((1.1216172965292541,2.2206198821180513E-8),(1.0929414090177318,1.1543697719880128))
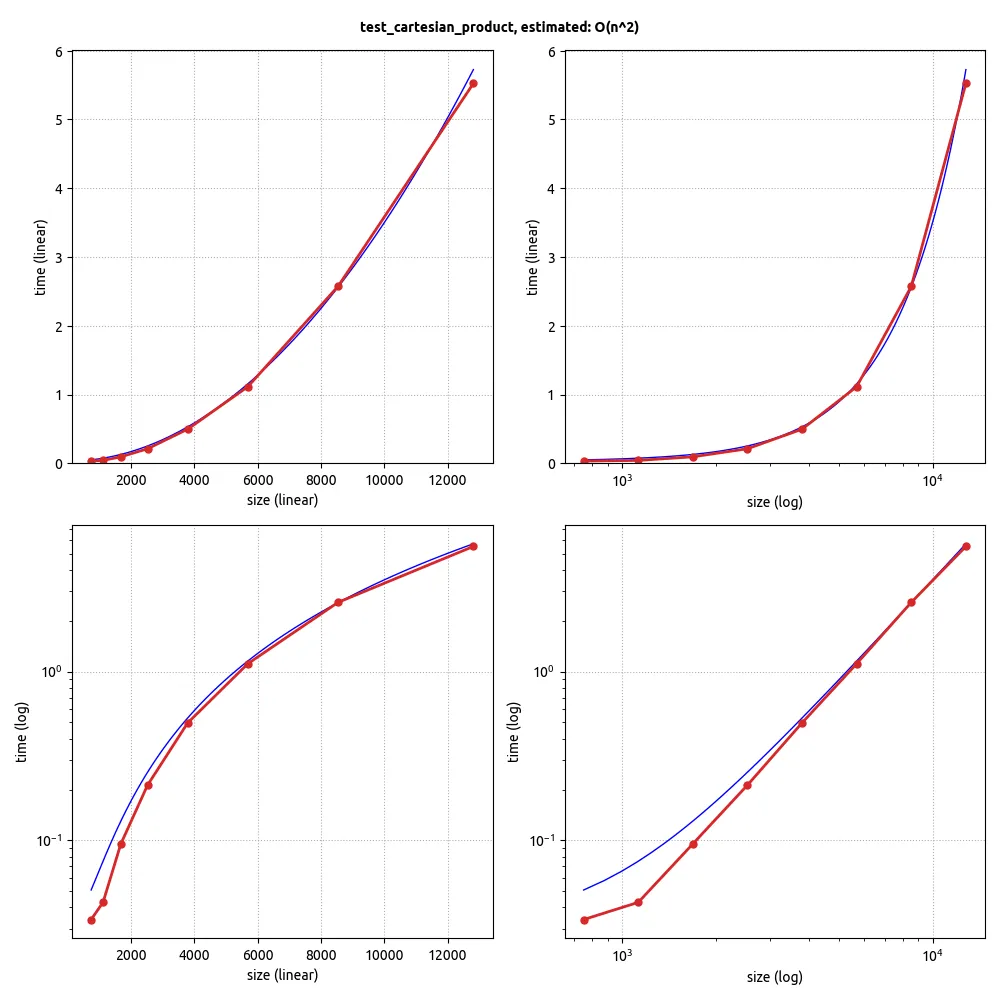
// Let's time something slow
def kube(n: Int) = (for (i <- 1 to n; j <- 1 to n; k <- 1 to n) yield 1).sum
val tl5 = new TimeLord(x=>x)(kube)
scala> tl5.alpha( tl5.multibench(10,100,0.1,10,10) )
res5: ((Double, Double), (Double, Double)) = ((2.8456382116915484,1.0433534274508799E-7),(2.6416659356198617,2.999094292838751))
// Okay, we're a little short of 3; there's constant overhead on the small sizes
无论如何,对于所述用例——检查订单是否更改——这可能是足够的,因为您可以在设置测试时稍微调整一下值,以确保它们给出合理的结果。也可以创建启发式算法来搜索稳定性,但这可能有点过度。
(顺便说一句,在这里没有明确的预热步骤;Theil-Sen估计器的强健拟合应该使其不必要适用于合理大的基准测试。这也是我不使用任何其他测试框架的原因;它所做的任何统计都会从这个测试中失去效力。)
再次编辑:如果你用以下方法替换alpha方法:
@inline private[this] def sq(x: Double) = x*x
final private[this] val inv_log_of_2 = 1/math.log(2)
@inline private[this] def log2(x: Double) = math.log(x)*inv_log_of_2
import math.{log,exp,pow}
case class Yp(x: Double, m: Double, b: Double) {}
case class Estimator(fx: Double => Double, invfx: Double=> Double, fy: (Double,Double) => Double, model: Yp => Double) {}
val alpha = Estimator(log, exp, (x,y) => log(y), p => p.b*pow(p.x,p.m))
val logalpha = Estimator(log, exp, (x,y) =>log(y/log2(x)), p => p.b*log2(p.x)*pow(p.x,p.m))
case class Fit(slope: Double, const: Double, bounds: (Double,Double), fracrms: Double) {}
def theilsen(data: Seq[(Int,Array[Double])], est: Estimator = alpha) = {
val dat = data.map{ case (i,ad) => ad.map(x => est.fx(i) -> est.fy(i,x)) }
val slopes = (for {
i <- dat.indices
j <- ((i+1) until dat.length)
(pi,px) <- dat(i)
(qi,qx) <- dat(j)
} yield (qx - px)/(qi - pi)).sorted
val mbest = slopes(slopes.length/2)
val mp05 = slopes(slopes.length/20)
val mp95 = slopes(slopes.length-(1+slopes.length/20))
val intercepts = dat.flatMap{ _.map{ case (li,lx) => lx - li*mbest } }.sorted
val bbest = est.invfx(intercepts(intercepts.length/2))
val fracrms = math.sqrt(data.map{ case (x,ys) => ys.map(y => sq(1 - y/est.model(Yp(x,mbest,bbest)))).sum }.sum / data.map(_._2.length).sum)
Fit(mbest, bbest, (mp05,mp95), fracrms)
}
然后,当有对数项时,您可以得到指数的估计值——误差估计存在于选择是使用对数项还是不使用对数项的正确方式之间,但由您决定(即我假设您最初将监督此过程并阅读输出的数字):
val tl3 = new TimeLord(x=>Vector.fill(x)(util.Random.nextInt))(_.sorted)
val timings = tl3.multibench(100,10000,0.1,10,10)
scala> tl3.theilsen( timings )
res20: tl3.Fit = Fit(1.1811648421030059,3.353753446942075E-8,(1.1100382697696545,1.3204652930525234),0.05927994882343982)
scala> tl3.theilsen( timings, tl3.logalpha )
res21: tl3.Fit = Fit(1.0369167329732445,9.211366397621766E-9,(0.9722967182484441,1.129869067913768),0.04026308919615681)
(编辑:修正了RMS计算,使其实际上是平均值,另外还演示了您只需要进行一次定时,然后可以尝试两种拟合。)