邻接表或边列表转换为面

Question

邻接表或边列表转换为面

4

如何从平面图的边界列表或邻接列表表示转换为面列表？

例如，对于这个图（奇怪的是它不是0索引）：

我想要一个看起来像这样的列表：

[
[1,2,8,7],
[1,2,4,3],
[1,3,5,7],
[2,4,6,8],
[5,6,7,8],
[3,4,6],
[3,5,6]
]

它不必采用那种格式或顺序，但应该是一种列出所有面孔的列表（或集合）。外部面孔也包括在内。

对于一个具有V个顶点的图形（因为是平面图，E=O(V)），该算法应该在O(V)内生成此列表。

- user4159038

邻接表按角度排序了吗？如果没有，它们可以排列吗？ - David Eisenstat

3个回答

1

短答案是：你必须实际布局图形！更确切地说，你必须在平面上找到图形的嵌入方式 - 假设没有边交叉。因此，你上面的嵌入方式是：

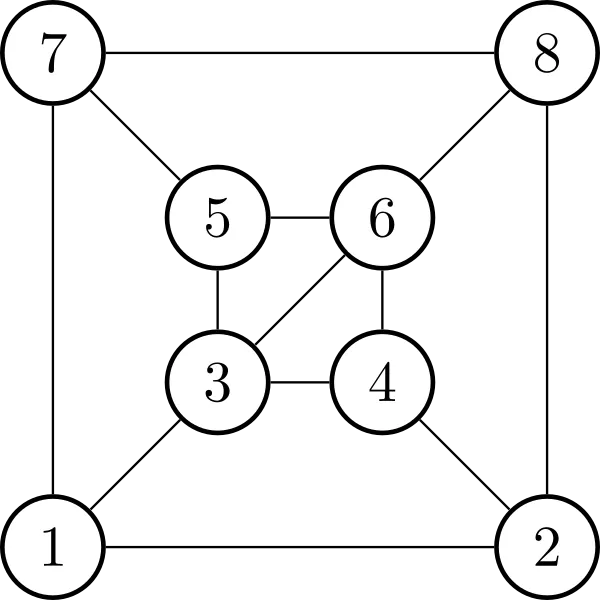
1: [2, 7, 3]
2: [1, 4, 8]
3: [1, 5, 6, 4]
...

这是每个顶点都有其邻居集的排序。您必须指定该排序是顺时针还是逆时针，但除此之外就没有其他要求了。

一旦您完成嵌入，就可以使用组合地图来恢复面。这看起来比实际情况要棘手，尽管它涉及到飞镖（或标志）。

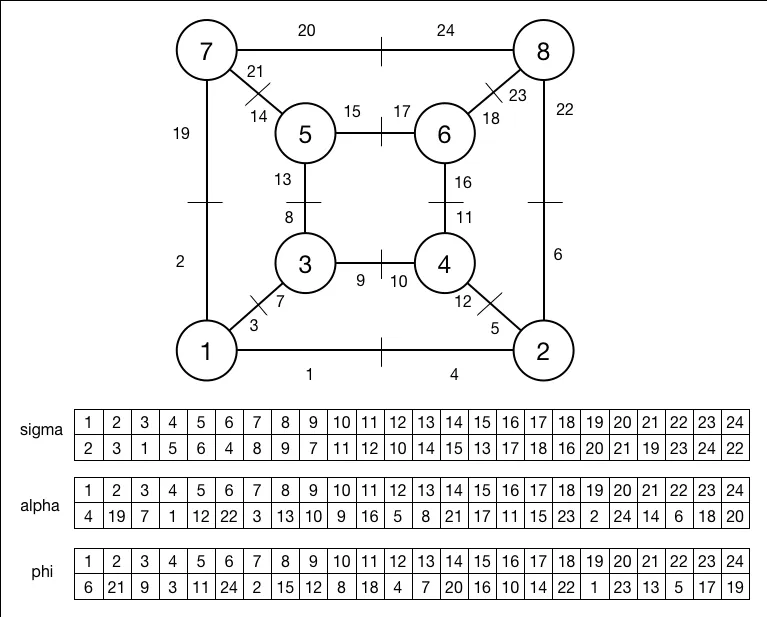
首先，将每个边缘分成标志（顶点+半边），并创建一个存储地图的排列（维基描述中的sigma）。例如，我们可以按照地图的相同顺序标记标志 - 然后1：[2、7、3]变为{1->2：1、1->7：2、1->3：3}等等。

例如，一个立方体（注意：删除了中间的边缘！）：

然后计算alpha（反演置换），它仅将标志映射到边缘另一侧的标志。最后，phi是这两个置换的乘积，phi的循环给出面。因此，从图像中的phi，我们得到(1, 6, 24, 19)，这是外部面（请注意，这些是darts，因此我们考虑它开始的顶点）。

- gilleain

0

正如@gilleain在他的回答中提到的，您必须实际布局图形，因为如果您只给定拓扑结构，则可能存在多个布局。在这里，我将进行一些算法分析，然后给出一个简单的解决方案。

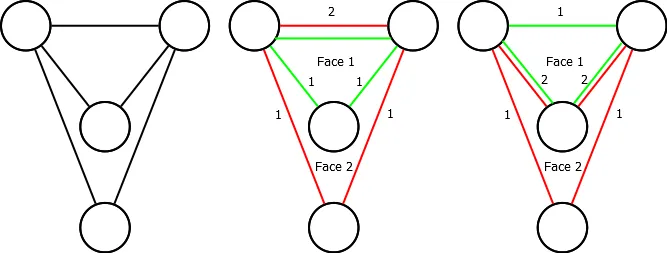
引理1：每条边涉及至少一个面，最多涉及两个面。

证明：我们在二维空间中绘图，所以一条线将平面分成两半。

这意味着我们可以为每条边附加一个“容量”，初始值为2。当我们发现涉及一条边的面时，从该容量中减去1。

由于面是平面图中的循环，因此问题转化为在给定上述约束条件的情况下找到循环。

引理2：如果我们检查两个有效解之间的差异，则它们在具有互补容量（1 vs. 2和2 vs. 1）的边上不同。

证明：见图。

因此，当你在寻找解决方案时排除了导致另一个解决方案的歧义，就会耗尽边缘的容量。

因此，直接的解决方案是在图中进行深度优先搜索以查找循环。当您找到一个循环时，请减去涉及边缘的容量。当容量达到0时，在DFS进一步时考虑删除该边缘。请注意，当发现一个循环时，我们必须检查其中所有边缘是否具有容量1。如果是这样，则必须跳过此循环，因为将此循环包含在我们的结果中会导致重复计数。

def DFS-Tarjan(v, capacities, stack)
    for e in N(v):
        if capacity[e] != 0:
            if stack.contains[e.target] AND NOT all of them have capacity 1:
                output-loop(stack, e.target)
                for e2 in stack:
                    capacity[e2] -= 1
            else:
                stack.push(e.target)
                DFS-Tarjan(v, capacities, stack)
                stack.pop(e.target)
        else:
            pass # capacity drained

def find-faces(g):
    initialize capacities of g.E to [2...2]
    for v in unvisited(g.V):
        DFS-Tarjan(v, capacities, [])

如果您更改DFS的顺序，则可以找到多个解决方案。对于单个解决方案，该算法的时间复杂度为O（V），因为每条边最多只被使用两次。

- Yadli

通过深度优先搜索查找环并不等同于查找面。你可以在 DFS 中找到一个环，然后将该环内部定义为一个区域，但是这个区域可能会被 DFS 中其他路径所划分，形成两个子区域，而这些子区域实际上就是由原始环和划分线段所定义的两个面。这个过程可以重复进行，直到所有面都被找到。 - MT0

1

请在您的解释中更详细地说明，因为目前它似乎没有意义，而且不清楚“引理2”证明了什么。您似乎严重依赖DFS处理边缘的顺序 - 如果这是非确定性的，则您的算法在一般情况下无法工作，除非进行大量准备工作来重新排序边缘的优先级。 - MT0

引理1只是约旦曲线定理的一个陈述。然而，一条边总是与恰好两个面相邻 - 您似乎只是忽略了嵌入的外部面。 - MT0

"e.target" 是类似于伪代码的 AND NOT all of them have capacity 1:，我认为最好只保留核心逻辑并剥离细节。 - Yadli

e.target 是伪代码...好的，但它代表什么？它是相邻顶点吗？它是DFS树中的祖先吗？还是其他什么？目前，我被你的伪代码缺乏清晰度打败了，无法开始实现你的算法以正确验证它。 - MT0

显示剩余7条评论

网页内容由stack overflow 提供, 点击上面的

可以查看英文原文，
原文链接

- MT0 · Accepted Answer

您需要生成一个图的平面嵌入。一个问题是经常会有一个双连通图可以生成多个平面嵌入。

其中一个测试平面性和嵌入算法在"Planarity Testing by Path Addition" PhD thesis中给出，它解决了生成一个双连通图的所有可能平面嵌入的问题（对于一个有V个顶点和E条边的双连通图，单个嵌入的时间和空间复杂度为O(V+E)，生成所有可能独特平面嵌入的时间复杂度为O(P(V+E))，空间复杂度为O(V+E)，其中P是嵌入的排列数）。

第5章详细介绍了测试图的平面性所需的算法，以及如何为每个顶点生成循环边序（也介绍了如何迭代到嵌入的下一个排列）。

给定一个循环边序，您可以通过取每条边并沿着循环边序中下一个顺时针（或逆时针）的边来遍历每个连续的顶点来生成图的面。