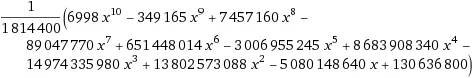为什么使用Math.pow的这段代码会打印出"HELLO WORLD"?

Question

我发现了下面的代码。我知道，它看起来比使用似乎随机的数字（此处）更不奇怪/令人兴奋，但似乎比在一个大数上使用位移（此处）更复杂：

long[] c = {130636800L, -5080148640L, 13802573088L, -14974335980L, 8683908340L,
           -3006955245L, 651448014L, -89047770L, 7457160L, -349165L, 6998L};

for (int x = 0; x < 11; x++) {
    long s = 0;
    for (int i = 0; i < 11; i++)
        s += c[i] * Math.pow(x, i);

    System.out.print((char)(s / 1814400));
}

在Ideone上的代码

输出:

你好，世界

它是如何工作的？它是一种加密形式还是有人发疯构建它了？

- honk

---

试试将整个计算反过来！这里没有什么神奇的东西，只是数字经历了一些计算。 - GhostCat

"它是如何工作的？" - 现在是铅笔和纸的时间了... - Mitch Wheat

我不会称之为“加密”，更多的是“混淆”。 - Fred Larson

没有人因此而发疯，但他们很可能有很多空闲时间。 :) 他们只是取出消息的每个代码点，对其应用一些操作，得到一个值，然后编写一个程序来反转这些操作以恢复原始代码点。有人很可能会在答案部分提供完整细节。 - Ray Toal

正如@FredLarson所说，这只是一种奇怪的混淆。字符本质上是数字，如果您传递正确的数字并将它们转换为字符，您可以打印任何内容。 - Jan Ossowski

Answer 1

让我们来看一些数学：

解下面的方程，你就能得到答案。这些方程只有一个唯一解，因为方程的数量等于未知变量的数量。

让 c[0] = 72，它是 'H' 的 ASCII 值。

为了清晰起见：我使用了 ^ 表示乘幂约定。现在解决：

1^0 * c[0] + 1^1 * c[1] + 1^2 * c[2] + 1^3 * c[3] + 1^4 * c[4] + 1^5 * c[5] + 1^6 * c[6] + 1^7 * c[7] + 1^8 * c[8] + 1^9 * c[9] + 1^10 * c[10] = 69
2^0 * c[0] + 2^1 * c[1] + 2^2 * c[2] + 2^3 * c[3] + 2^4 * c[4] + 2^5 * c[5] + 2^6 * c[6] + 2^7 * c[7] + 2^8 * c[8] + 2^9 * c[9] + 2^10 * c[10] = 76
3^0 * c[0] + 3^1 * c[1] + 3^2 * c[2] + 3^3 * c[3] + 3^4 * c[4] + 3^5 * c[5] + 3^6 * c[6] + 3^7 * c[7] + 3^8 * c[8] + 3^9 * c[9] + 3^10 * c[10] = 76
4^0 * c[0] + 4^1 * c[1] + 4^2 * c[2] + 4^3 * c[3] + 4^4 * c[4] + 4^5 * c[5] + 4^6 * c[6] + 4^7 * c[7] + 4^8 * c[8] + 4^9 * c[9] + 4^10 * c[10] = 79
5^0 * c[0] + 5^1 * c[1] + 5^2 * c[2] + 5^3 * c[3] + 5^4 * c[4] + 5^5 * c[5] + 5^6 * c[6] + 5^7 * c[7] + 5^8 * c[8] + 5^9 * c[9] + 5^10 * c[10] = 32
6^0 * c[0] + 6^1 * c[1] + 6^2 * c[2] + 6^3 * c[3] + 6^4 * c[4] + 6^5 * c[5] + 6^6 * c[6] + 6^7 * c[7] + 6^8 * c[8] + 6^9 * c[9] + 6^10 * c[10] = 87  
7^0 * c[0] + 7^1 * c[1] + 7^2 * c[2] + 7^3 * c[3] + 7^4 * c[4] + 7^5 * c[5] + 7^6 * c[6] + 7^7 * c[7] + 7^8 * c[8] + 7^9 * c[9] + 7^10 * c[10] = 79  
8^0 * c[0] + 8^1 * c[1] + 8^2 * c[2] + 8^3 * c[3] + 8^4 * c[4] + 8^5 * c[5] + 8^6 * c[6] + 8^7 * c[7] + 8^8 * c[8] + 8^9 * c[9] + 8^10 * c[10] = 82  
9^0 * c[0] + 9^1 * c[1] + 9^2 * c[2] + 9^3 * c[3] + 9^4 * c[4] + 9^5 * c[5] + 9^6 * c[6] + 9^7 * c[7] + 9^8 * c[8] + 9^9 * c[9] + 9^10 * c[10] = 76
10^0 * c[0] + 10^1 * c[1] + 10^2 * c[2] + 10^3 * c[3] + 10^4 * c[4] + 10^5 * c[5] + 10^6 * c[6] + 10^7 * c[7] + 10^8 * c[8] + 10^9 * c[9] + 10^10 * c[10] = 68

请注意，未知数的数量为c[1]到c[10]，共有10个。我们已知c[0] = 72，所以它不是未知数，方程的数量是10。

现在，我们将所有数字乘以1814400，除以答案中的相同数字，这样不会改变任何内容，或者通过解决方程得出的答案可能不是整数，因此乘以1814400以获得整数。

您可以使用此代码解决任意阶数的同时方程。

- user9823668

Answer 2

受到用户9823668的回答的启发，我找到了另一种逆向计算的方法。代码中的内循环（包括输出行的除法）基本上代表了以下多项式：

这个多项式在代码的外层循环中针对0到10的值进行计算，并产生相应的ASCII字符。因此问题是：如何通过给定的连续数据点拟合一个多项式?

我的搜索结果之一指向术语牛顿插值多项式。这是一种针对给定数据点的插值多项式。由于该多项式是针对值0到10进行计算的，因此我们在这里有xi = i的特殊情况。因此，为了构造上述多项式，我们必须计算一些二项式系数。

首先，我们必须计算数据点上的差商（即ASCII编码的函数输出）：

 0: H = <b>72</b>
 1: E = 69  <b>-3</b>
 2: L = 76   7  <b>10</b>
 3: L = 76   0  -7  <b>-17</b>
 4: O = 79   3   3   10   <b>27</b>
 5:   = 32 -47 -50  -53  -63  <b>-90</b>
 6: W = 87  55 102  152  205  268   <b>358</b>
 7: O = 79  -8 -63 -165 -317 -522  -790 <b>-1148</b>
 8: R = 82   3  11   74  239  556  1078  1868  <b>3016</b>
 9: L = 76  -6  -9  -20  -94 -333  -889 -1967 -3835 <b>-6851</b>
10: D = 68  -8  -2   7    27  121   454  1343  3310  7145 <b>13996</b>

然后，每列中最顶部的条目是我们构建插值多项式所需的系数：

72
-     3 /       1 x
+    10 /       2 x(x-1)
-    17 /       6 x(x-1)(x-2)
+    27 /      24 x(x-1)(x-2)(x-3)
-    90 /     120 x(x-1)(x-2)(x-3)(x-4)
+   358 /     720 x(x-1)(x-2)(x-3)(x-4)(x-5)
-  1148 /    5040 x(x-1)(x-2)(x-3)(x-4)(x-5)(x-6)
+  3016 /   40320 x(x-1)(x-2)(x-3)(x-4)(x-5)(x-6)(x-7)
-  6851 /  362880 x(x-1)(x-2)(x-3)(x-4)(x-5)(x-6)(x-7)(x-8)
+ 13996 / 3628800 x(x-1)(x-2)(x-3)(x-4)(x-5)(x-6)(x-7)(x-8)(x-9)

这里，分母表示n!（见特殊情况）。通过展开这个公式（例如使用WolframAlpha），您可以得到上面显示的多项式。如果有人想知道，这个多项式如下所示：

- honk