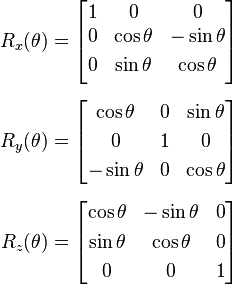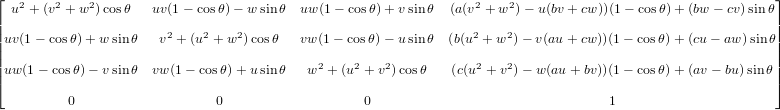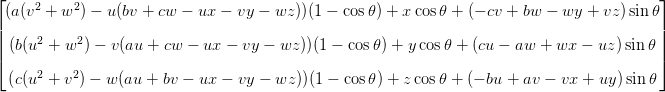一种有用的进行旋转的方法是使用
四元数。实际上,我发现它们更容易使用,并且有避免
万向锁的额外好处。
这里有一个很好的教程,解释了为什么以及如何将其用于绕任意轴旋转(这是对用户问题的回答)。它有点高级,适合初学者,所以我建议从那里开始。
更新以避免链接失效
来自链接网站的文本:
显然,绕过原点和三维空间中单位球面上的一点
(a,b,c)的轴旋转是一个线性变换,因此可以通过矩阵乘法表示。我们将介绍一种非常简洁的确定该矩阵的方法,但为了欣赏公式的紧凑性,最好先做一些说明。
三维旋转是一种非常特殊的线性变换,其中最重要的特点是保持向量长度和向量之间的角度(当两个向量被旋转时)。这样的变换被称为“正交变换”,它们由正交矩阵表示:
M M' = I
我们方便地用“'”来表示转置。换句话说,正交矩阵的转置是其逆矩阵。
考虑定义变换所需的数据。您已经给出了旋转轴的符号表示,ai + bj + ck,方便地假定为单位向量。唯一的其他数据是旋转角度,由于没有更自然的字符,我将其表示为r(表示旋转?),并且我们将假定以弧度给出。
现在,即使在正交变换中,旋转也是有点特殊的,事实上,由于它们具有保持“方向”的属性,它们也被称为特殊正交变换(或矩阵)。将它们与反射进行比较,后者也可以保持长度和角度,您会发现保持方向(或“左右手性”,如果您愿意)的几何特征在矩阵的行列式中具有数值对应关系。旋转矩阵的行列式为1,而反射矩阵的行列式为-1。结果表明,两个旋转的乘积(或组合)仍然是一个旋转,这与乘积的行列式等于行列式的乘积(或旋转的情况下为1)的事实相符。
现在我们可以描述一种逐步的方法,来构建所需的矩阵(在我们快速跳到答案之前!)。首先考虑旋转单位向量的步骤:
u = ai + bj + ck
希望将其与“标准”单位向量之一重合,可能是k(正z轴)。现在我们知道如何围绕z轴旋转;这只是在x、y坐标上进行通常的2x2变换的问题:
cos(r) sin(r) 0
M = -sin(r) cos(r) 0
0 0 1
最后,我们需要“撤销”将u旋转到k的初始旋转,这很容易实现,因为该转换的逆转换(我们回想起)由矩阵转置表示。换句话说,如果矩阵R表示将u旋转到k的旋转,则R'将k旋转到u,并且我们可以像这样写出变换的组合:
R' M R
很容易验证这个矩阵乘积,当它与向量u相乘时,会得到u本身:
R' M R u = R' M k = R' k = u
因此,这确实是绕由u定义的轴旋转。
这种表达式的一个优点是,它清晰地将M对角度r的依赖性与Q和Q'对“轴”向量u的依赖性分离开来。然而,如果我们需要详细进行计算,我们显然需要进行大量的矩阵乘法。
所以,来看一下快捷方式。当所有的尘埃落定时,旋转之间的乘法等同于单位四元数的乘法。四元数,如果你以前没有见过,是复数的四维推广。它们是由威廉·哈密顿(William Hamilton)在1843年“发明”的:
[威廉·罗恩·哈密顿]
http://www-gap.dcs.st-and.ac.uk/~history/Mathematicians/Hamilton.html
今天的三维图形程序员非常感激他。
每个单位四元数q=q0+q1*i+q2*j+q3*k都可以定义一个旋转矩阵。
(q0² + q1² - q2² - q3²) 2(q1q2 - q0q3) 2(q1q3 + q0q2)
Q = 2(q2q1 + q0q3) (q0² - q1² + q2² - q3²) 2(q2q3 - q0q1)
2(q3q1 - q0q2) 2(q3q2 + q0q1) (q0² - q1² - q2² + q3²)
验证Q是否为正交矩阵,即
Q Q' = I,实质上意味着Q的行形成一个标准正交基。例如,第一行应该长度为1:
(q0² + q1² - q2² - q3²)² + 4(q1q2 - q0q3)² + 4(q1q3 + q0q2)²
= (q0² + q1² - q2² - q3²)² + 4(q1q2)² + 4(q0q3)² + 4(q1q3)² + 4(q0q2)²
= (q0² + q1² + q2² + q3²)²
= 1
前两行的点积应该为零:
[ (q0² + q1² - q2² - q3²), 2(q1q2 - q0q3), 2(q1q3 + q0q2) ]
* [ 2(q2q1 + q0q3), (q0² - q1² + q2² - q3²), 2(q2q3 - q0q1) ]
= 2(q0² + q1² - q2² - q3²)(q2q1 + q0q3)
+ 2(q1q2 - q0q3)(q0² - q1² + q2² - q3²)
+ 4(q1q3 + q0q2)(q2q3 - q0q1)
= 4(q0²q1q2 + q1²q0q3 - q2²q0q3 - q3²q2q1)
+ 4(q3²q1q2 - q1²q0q3 + q2²q0q3 - q0²q2q1)
= 0
一般情况下,可以证明det(Q) = 1,因此Q确实是一个旋转。
但是,Q的旋转轴在哪个方向?旋转角度是多少?给定角度r和单位向量:
u = ai + bj + ck
如前所述,相应的四元数为:
q = cos(r/2) + sin(r/2) * u
= cos(r/2) + sin(r/2) ai + sin(r/2) bj + sin(r/2) ck
因此,使用:
q0 = cos(r/2), q1 = sin(r/2) a, q2 = sin(r/2) b, q3 = sin(r/2) c,
我们能够得到所需的属性,即Q乘以u会“固定”它。
Q u = u
不要费力地通过冗长的代数计算,让我们来做一个简单的例子。
令u = 0i + 0.6j + 0.8k成为我们的单位向量,r = pi成为我们的旋转角度。
那么四元数就是:
q = cos(pi/2) + sin(pi/2) * u
= 0 + 0i + 0.6j + 0.8k
和旋转矩阵:
-1 0 0
Q = 0 -0.28 0.96
0 0.96 0.28
在这个具体的案例中,很容易验证 Q Q' = I 并且 det(Q) = 1。
同时我们计算出:
Q u = [ 0, -0.28*0.6 + 0.96*0.8, 0.96*0.6 + 0.28*0.8 ]'
= [ 0, 0.6, 0.8 ]'
= u
例如,单位向量u定义了旋转轴,因为它被Q“固定”。
最后,我们通过考虑Q如何作用于沿着正x轴方向的单位向量(与u垂直)来说明旋转角度为pi(或180度):
i + 0j + 0k, or as a vector, [ 1, 0, 0 ]'
接下来是关于编程的内容,Q [ 1, 0, 0 ]' = [-1, 0, 0 ]'表示将向量[1,0,0]'绕着向量u旋转π角度。
关于用四元数表示旋转的方法和其他表示方法(以及它们的优点),可以参考以下链接:
[三维旋转的表示方法]http://gandalf-library.sourceforge.net/tutorial/report/node125.html
总结
给定弧度r和单位向量u=ai+bj+ck或[a,b,c]', 定义如下:
q0 = cos(r/2), q1 = sin(r/2) a, q2 = sin(r/2) b, q3 = sin(r/2) c
并从这些值构建旋转矩阵:
(q0² + q1² - q2² - q3²) 2(q1q2 - q0q3) 2(q1q3 + q0q2)
Q = 2(q2q1 + q0q3) (q0² - q1² + q2² - q3²) 2(q2q3 - q0q1)
2(q3q1 - q0q2) 2(q3q2 + q0q1) (q0² - q1² - q2² + q3²)
使用 Q 进行乘法,然后实现所需的旋转,特别地:
Q u = u

![\hat{u} = [u_x,u_y,u_z]](https://istack.dev59.com/HoLjl.webp)
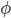
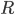
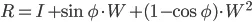
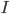
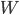
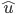
![W= [0 -uz uy; uz 0 -ux; -uy ux 0];](https://istack.dev59.com/V1Fk9.webp)