经纬度点集间的最大距离

Question

经纬度点集间的最大距离

ralgorithmgeospatiallatitude-longitudecran

15

我有一组经纬度坐标。如何高效地计算集合中任意两个点之间的最大距离（如果您愿意，称之为“最大直径”）？

一种朴素的方法是使用Haversine公式来计算每两个点之间的距离并获取最大值，但这显然不具有可扩展性。

编辑：这些点位于一个足够小的区域内，测量范围是人们在单日活动中携带移动设备的区域。

- Jeroen Ooms

如果距离“较小”（例如，几十英里/公里），则简单的公式将为解决方案提供更好的常数因子。 - Walter Tross

你能举个例子吗？ - Jeroen Ooms

最接近和最远的问题在你的问题和那个问题之间应该是微不足道的区别。 - hatchet - done with SOverflow

2

请参考sp包中的?spDists，以及geosphere包中的其他选项来计算距离。 - mdsumner

1

@hatchet：最接近与最远并不是一个微不足道的差别。 - Walter Tross

显示剩余2条评论

4个回答

10

我认为以下内容可能是一个有用的近似值，它与点的数量呈线性比例而不是二次比例，并且非常容易实现：

1. 计算点的质心M 2. 找到距离M最远的点P0 3. 找到距离P0最远的点P1 4. 用P0和P1之间的距离来近似最大直径

这可以通过重复第3步N次并取P_N-1和P_N之间的距离来推广。

第1步可以有效地进行，将M近似为经度和纬度的平均值，当距离“小”且极点足够远时，这是可以接受的。其他步骤可以使用精确的距离公式进行，但如果点的坐标可以近似为在一个平面上，则速度要快得多。一旦找到了“远距离对”（希望是具有最大距离的对），则可以使用精确公式重新计算其距离。

一个近似的例子可能是以下内容：如果φ(M)和λ(M)是质心的纬度和经度，计算为Σφ(P)/n和Σλ(P)/n，

x(P) = (λ(P) - λ(M) + C) cos(φ(P))
y(P) = φ(P) - φ(M) [这只是为了清晰起见，也可以简单地写成y(P) = φ(P)]

其中C通常为0，但如果点集穿过λ=±180°线，则可以为±360°。要找到最大距离，您只需找到

max((x(P_N) - x(P_N-1))² + (y(P_N) - y(P_N-1))²)

（您不需要平方根，因为它是单调的）

同样的坐标变换可以用于重复步骤1（在新的坐标系统中），以获得更好的起点。我怀疑，如果满足某些条件，则上述步骤（不重复步骤3）总是导致“真实的远距离对”（我的术语）。如果我只知道哪些条件...

编辑：

我讨厌在别人的解决方案基础上进行构建，但有人必须这样做。

仍然保持以上4个步骤，可选（但可能有益，取决于点的典型分布）重复步骤3，并遵循Spacedman的解决方案，在三维中进行计算克服了靠近和远离极点的限制：

x（P）= sin（φ（P））
y（P）= cos（φ（P））sin（λ（P））
z（P）= cos（φ（P））cos（λ（P））

（唯一的近似是这仅适用于完美的球体）

质心由公式x(M) = Σx(P)/n给出，等等，而要寻找的最大值是

max((x(P_N) - x(P_N-1))² + (y(P_N) - y(P_N-1))² + (z(P_N) - z(P_N-1))²)

所以：首先将球坐标转换为直角坐标，然后从质心开始，至少在两个步骤（步骤2和3）中找到距离前一个点最远的点。您可以重复步骤3，只要距离增加，可能有最大重复次数，但这不会使您远离局部最大值。如果点分布在整个地球上，则从质心开始也没有太大帮助。

编辑2：

我学会了足够的R语言来写下算法的核心（用于数据分析的好语言！）

对于平面近似，忽略λ=±180°线周围的问题：

# input: lng, lat (vectors)
rad = pi / 180;
x = (lng - mean(lng)) * cos(lat * rad)
y = (lat - mean(lat))
i = which.max((x - mean(x))^2 + (y       )^2)
j = which.max((x - x[i]   )^2 + (y - y[i])^2)
# output: i, j (indices)

在我的电脑上，查找1000000个点的索引i和j只需要不到一秒钟。下面的3D版本稍微慢一些，但适用于任何点的分布（并且不需要在穿过λ=±180°线时进行修改）：

# input: lng, lat
rad = pi / 180
x = sin(lat * rad)
f = cos(lat * rad)
y = sin(lng * rad) * f
z = cos(lng * rad) * f
i = which.max((x - mean(x))^2 + (y - mean(y))^2 + (z - mean(z))^2)
j = which.max((x - x[i]   )^2 + (y - y[i]   )^2 + (z - z[i]   )^2)
k = which.max((x - x[j]   )^2 + (y - y[j]   )^2 + (z - z[j]   )^2) # optional
# output: j, k (or i, j)

计算 k 可以被省略（即结果可以由 i 和 j 给出），这取决于数据和要求。另一方面，我的实验表明，计算进一步的指数是无用的。

应该记住，在任何情况下，得到的点之间的距离都是一个估计值，它是集合“直径”的下限，尽管它往往会是直径本身（有多少次取决于数据）。 编辑3： 不幸的是，平面逼近的相对误差在极端情况下可能高达1-1/√3 ≅ 42.3%，即使非常罕见也可能是不可接受的。可以修改算法，以获得大约20%的上限，我用圆规和直尺推导出来的（解析解决方案很麻烦）。修改后的算法找到一对具有局部最大距离的点，然后重复相同的步骤，但这次从第一对的中点开始，可能会找到另一对：

# input: lng, lat
rad = pi / 180
x = (lng - mean(lng)) * cos(lat * rad)
y = (lat - mean(lat))
i.n_1 = 1 # n_1: n-1
x.n_1 = mean(x)
y.n_1 = 0 # = mean(y)
s.n_1 = 0 # s: square of distance
repeat {
   s = (x - x.n_1)^2 + (y - y.n_1)^2
   i.n = which.max(s)
   x.n = x[i.n]
   y.n = y[i.n]
   s.n = s[i.n]
   if (s.n <= s.n_1) break
   i.n_1 = i.n
   x.n_1 = x.n
   y.n_1 = y.n
   s.n_1 = s.n
}
i.m_1 = 1
x.m_1 = (x.n + x.n_1) / 2
y.m_1 = (y.n + y.n_1) / 2
s.m_1 = 0
m_ok  = TRUE
repeat {
   s = (x - x.m_1)^2 + (y - y.m_1)^2
   i.m = which.max(s)
   if (i.m == i.n || i.m == i.n_1) { m_ok = FALSE; break }
   x.m = x[i.m]
   y.m = y[i.m]
   s.m = s[i.m]
   if (s.m <= s.m_1) break
   i.m_1 = i.m
   x.m_1 = x.m
   y.m_1 = y.m
   s.m_1 = s.m
}
if (m_ok && s.m > s.n) {
   i = i.m
   j = i.m_1
} else {
   i = i.n
   j = i.n_1
}
# output: i, j

这个三维算法可以以类似的方式进行修改。在二维和三维情况下，如果找到第二对点，可以再次从中点开始重新开始。在这种情况下，上限留给读者自行思考。

修改后的算法与（过于）简单的算法进行比较，对于正常和方形均匀分布，处理时间几乎翻倍，并且平均误差从0.6％降低到0.03％（数量级）。从中点重新开始会导致稍微更好的平均误差，但最大误差几乎相等。

编辑4：

我还需要研究这篇文章，但看起来用圆规和直尺找到的20％实际上是1-1/√（5-2√3）≅ 19.3％

- Walter Tross

也许您可以提供一个小的实际示例，展示如何在 r 中实现这个功能？（这是原帖作者试图实现的编程语言）。 - Simon O'Hanlon

@SimonO101：抱歉，我不懂 R :-( - Walter Tross

3

现在我会一点R语言了 :-) - Walter Tross

太好了！很高兴听到这个好的解决方案和算法。我给你点赞。 - Simon O'Hanlon

谢谢。快速简单的近似方法，非常适合我的问题。最终距离可以使用 geosphere::distHaversine(c(lat[i], lng[i]), c(lat[j], lng[j])) 计算。 - Jeroen Ooms

@Jeroen：永远不要接受陌生人的代码，除非它经过彻底的测试和审查；-）在您接受我的答案之后，我开始担心您或其他人可能会在生产中使用我的代码。因此，我进行了一些真正的测试，并使用指南针和直尺进行了一些真正的工作。为了修复我发现的问题，我不得不修改算法，这使得平均时间增加了近一倍，但让我睡得更好（也许您也是）。 - Walter Tross

3

这是一个天真的例子，不太适用于大规模应用（正如你所说），但可能有助于在R中构建解决方案。

## lonlat points
n <- 100
d <- cbind(runif(n, -180, 180), runif(n, -90, 90))


library(sp)
## distances on WGS84 ellipsoid
x <- spDists(d, longlat = TRUE)

## row, then column index of furthest points
ind <- c(row(x)[which.max(x)], col(x)[which.max(x)])

## maps
library(maptools)
data(wrld_simpl)
plot(as(wrld_simpl, "SpatialLines"), col = "grey")

points(d, pch = 16, cex = 0.5)

## draw the points and a line between  on the page
points(d[ind, ], pch = 16)
lines(d[ind, ], lwd = 2)


## for extra credit, draw the great circle on which the furthest points lie
library(geosphere)


lines(greatCircle(d[ind[1], ], d[ind[2], ]), col = "firebrick")

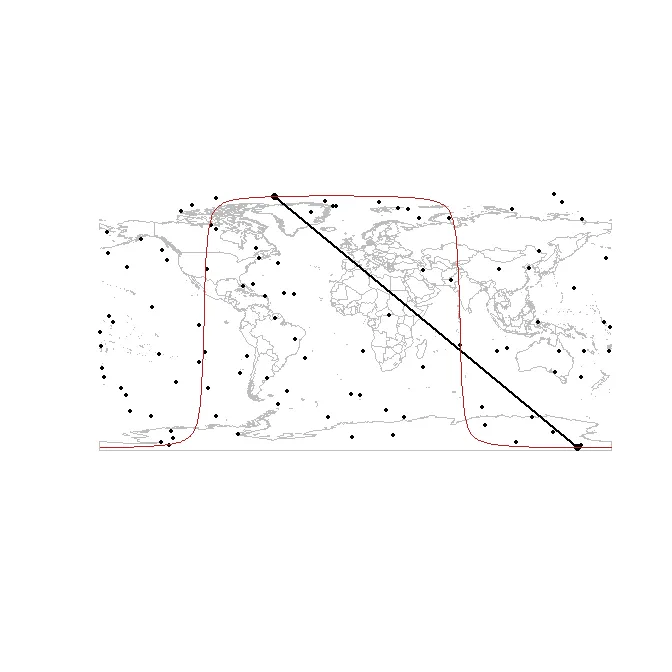
在WGS84椭球体上查找样本点之间的最远距离

如果需要更多的距离计算选项，可以使用geosphere包。在这里使用的详细信息请参见sp中的?spDists。

- mdsumner

+1 以展示 sp 和 geosphere 机制。我觉得对于大量的点，最快的搜索可能是将地球表面分成一个网格；计算所有占用的网格单元格（使用它们的顶点）之间的最小和最大距离；仅保留在彼此完全远离任何其他单元格的单元格集合中的点；然后细分它们，重复步骤2、3和4，直到点的数量已经足够减少。需要大量的簿记工作，但在大多数情况下应该可以运行得非常快。 - Josh O'Brien

我也有类似的想法，你可以很容易地用光栅图来粗略处理它，但今天不是我做这个的时候。这是一个好问题，希望我有机会探索一些这些想法（和沃尔特的想法）。我在20000个点上尝试了一下，它可以正常运行，但非常浪费资源，而50000个点对于16Gb的内存来说太多了。 :) - mdsumner

3

您没有告诉我们这些点是否位于地球的一个足够小的部分。对于真正全局的点集，我的第一个猜测是运行一个朴素的O(n^2)算法，可能通过一些空间索引（R *树、八叉树等）获得性能提升。这个想法是预先生成一个n*（n-1）的距离矩阵中三角形列表，并将其分块输入快速距离库以最小化I/O和过程开销。Haversine很好，你也可以用Vincenty的方法来做（最大的贡献者是二次复杂度，而不是Vincenty公式中的（固定数量的）迭代）。顺便说一下，实际上，你不需要R来做这件事。

编辑#2：Barequet-Har-Peled algorithm（由Spacedman在他的回复中指出）对于e>0具有O（（n+1/（e^3））log（1/e））的复杂度，值得探索。

对于准平面问题，这被称为“凸包直径”，由三部分组成：

使用Graham扫描计算凸包，其时间复杂度为O(n*log(n)) - 实际上，应该尝试将点转换为横向墨卡托投影（使用数据集中的点的重心）。
通过旋转卡壳算法找到反极点 - 线性O(n)。
在所有反极点对中找到最大距离 - 线性搜索，O(n)。

伪代码和讨论链接：http://fredfsh.com/2013/05/03/convex-hull-and-its-diameter/

请参阅此处有关相关问题的讨论：https://gis.stackexchange.com/questions/17358/how-can-i-find-the-farthest-point-from-a-set-of-existing-points

编辑：Spacedman的解决方案指向了Malandain-Boissonnat算法（请参见pdf中的论文here）。然而，这比暴力朴素O(n ^ 2)算法更糟或相同。

- Deer Hunter

网页内容由stack overflow 提供, 点击上面的

可以查看英文原文，
原文链接

- Spacedman · Accepted Answer

定理 #1：地球表面上任意两个大圆距离的排序方式与你通过地球中心挖隧道的两个点之间的直线距离排序方式相同。

因此，将你的经纬度转换为基于球面的x、y、z坐标系或具有给定形状参数的椭球体。对于每个点只需使用一些正弦/余弦函数（不是每对点）。

现在你有了一个标准的三维问题，它不依赖于计算Haversine距离。两点之间的距离只是欧几里得距离（3D平方和的平方根）。如果只关心比较，可以省略平方根。

可能会有一些高级的空间树数据结构来帮助处理这个问题。或者像这里的算法（点击“下一页”查看3D方法）。或者使用这里的C++代码。

找到最大距离对后，可以使用Haversine公式计算该对点之间的地表距离。