logo标签列表

从（1..n）的自然数序列中取出每个第k个元素

algorithmsearchdata-structuresjosephus
7
例如，我们有一系列数字：1、2、3、4、5。我们每次取三个元素 => 3、1、5、2、4（选中的元素不应保留，我们可以在序列不为空时取）。使用双向循环链表的朴素实现不是一个好的选择，因为它的性能不佳。您能否给我建议，哪些数据结构和算法更适用？
2
链表有什么问题吗？看起来这里是自然的选择——一旦你选择了一个元素，只需将其从列表中删除（O(1)），然后继续。 - SomeWittyUsername
1
@SomeWittyUsername，n的上限是100,000。假设k也等于100,000。对于每个取出的元素，我们必须遍历100,000个元素。总操作数为10^10。时间限制为1秒。显然，我们会得到时间限制异常（这个任务来自比赛）。 - Evgeniy
我明白了。所以你需要一些额外的数据结构来快速地在列表中向前移动。 - SomeWittyUsername
1
@SomeWittyUsername 这是个问题。我不知道要使用哪种数据结构以及如何使用它。 - Evgeniy
一棵二叉树，每个分支都存储其左侧有多少叶子？您可以找到一个叶子，删除它，并一次性更新节点中的数字，从而获得N.logN而不是N²。（与此相反：https://dev59.com/cJnga4cB1Zd3GeqPfOib#38985607） - m69 ''snarky and unwelcoming''
显示剩余3条评论
4个回答
6

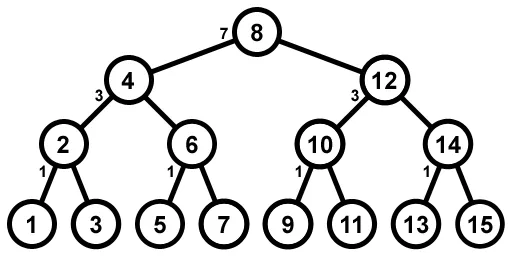
构建一个包含数字1到n的完全二叉树，例如对于n=15，二叉树如下：

start

在每个分支中，存储其左侧节点的数量；这将使我们能够快速找到第i个节点。(您会发现，此树具有非常可预测的结构和值，并且生成它比使用随机排序值构建相同大小的二叉树更有效。它也是一个理想的数组中树的候选项。) 然后，要查找第i个数字，请从根节点开始，在每个节点上，如果i比左侧节点的数量多1，则找到了第i个数字，否则向左（如果i不大于左侧节点数）或向右（如果i比左侧节点数多1）。
每当您向左移动时，请减少该节点左侧的节点计数（因为我们将删除一个节点）。
每当您向右移动时，请将您要查找的数字减去节点左侧的节点数加1（如果节点中的值已被删除，则加0）。
当你找到第i个节点时，读取它的值（添加到删除顺序列表中），然后将其值设置为0。此后，如果我们正在寻找的第i个节点已经被删除，我们将向右移动，然后取最左边的节点。
我们从一个值i = k开始，每次擦除第i个节点中的数字时，我们将减少总节点数并设置i =（i + k-1）％total（或者如果为零：i = total）。
这样可以获得log2N的查找时间和N×LogN的总复杂度。

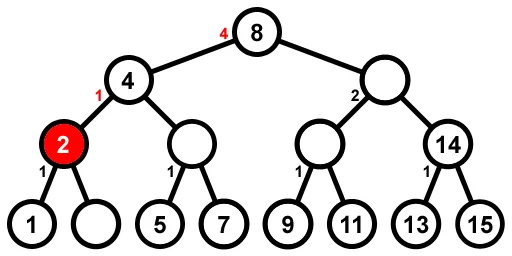
示例步骤：当n=15（如上图所示）且k=6时，前几步为6、12、3、10、2。此时的情况是：

step 5: number 2

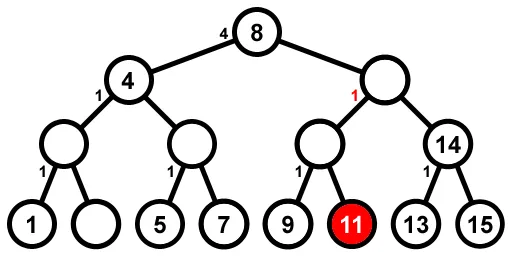
我们刚刚删除了第二个数字，现在 i = 2 + 6 - 1 = 7。我们从根节点开始，它左边有4个节点并且仍然有它的值，所以我们向右走并且从我们正在寻找的7中减去5得到2。我们到达节点12（已被删除）并发现它左边有2个节点，所以我们减少了它左边的节点数然后向左走。我们来到节点10（已被删除）并发现它左边有1个节点，而且1 = 2 - 1，所以这就是我们要找的节点；但是，由于它的值已被删除，我们向右走并从我们正在寻找的2中减去1得到1。我们到达节点11，它左边没有节点（因为它是叶子节点），0 = 1 - 1，所以这就是我们要找的节点。

step 6: number 11

我们将节点总数从10减少到9，将i从7更新为(7 + 6 - 1) % 9 = 3，然后继续查找第三个节点（现在值为5）。
以下是JavaScript的简单实现。它可以在不到一秒钟的时间内解决100,000个数字的系列问题，通过使用树形数组结构，可能可以使其更快速和更节省空间。（与上面的解释不同，数字的索引是从零开始的，以简化代码; 因此，索引0是树中的第一个数字，并且我们查找具有左侧连接子节点数等于目标索引的节点。） 

function Tree(size) {                      // CONSTRUCTOR
    var height = Math.floor(Math.log(size) / Math.log(2));
    this.root = addNode(height, 1 << height, size);
    this.size = size;
    function addNode(height, value, max) { // RECURSIVE TREE-BUILDER
        var node = {value: value > max ? 0 : value, lower: (1 << height) - 1};
        if (height--) {
            node.left = addNode(height, value - (1 << height), max);
            if (value < max) {             // DON'T ADD UNNECESSARY RIGHT NODES
                node.right = addNode(height, value + (1 << height), max);
            }
        }
        return node;
    }
}
Tree.prototype.cut = function(step) {      // SEE ANSWER FOR DETAILS
    var sequence = [], index = (step - 1) % this.size;
    while (this.size) {
        var node = this.root, target = index;
        while (node.lower != target || node.value == 0) {
            if (target < node.lower) {
                --node.lower;
                node = node.left;
            } else {
                target -= node.lower + (node.value ? 1 : 0);
                node = node.right;
            }
        }
        sequence.push(node.value);
        node.value = 0;
        index = (index + step - 1) % --this.size;
    }
    return sequence;
}
var tree = new Tree(15);
var sequence = tree.cut(6);
document.write("15/6&rarr;" + sequence + "<BR>");

tree = new Tree(100000);
sequence = tree.cut(123456);
document.write("100000/123456&rarr;" + sequence);

注意：

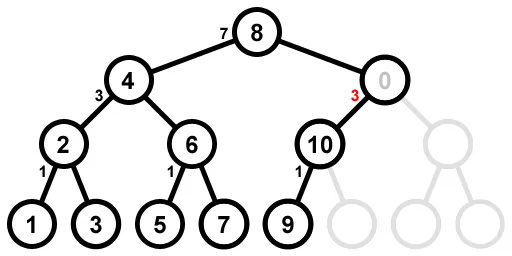
如果您查看n=10的树，您会发现根节点右侧的节点有一个不完整的树，其左侧有2个节点，但是上面代码示例中实现的算法将其左节点计数错误地设置为3而不是2：

tree for n=10

然而，左侧树不完整的节点从不持有任何值，并且从未存在右侧节点。因此，你总是在那里向左走，左侧节点数过高对结果没有影响。
这是二叉搜索树的一个惊人应用。另一种方法是使用基于策略的数据结构，您可以在此处阅读更多信息。其思想是使用其order_of_key()函数，从而节省了实现BST所需的时间。 - Milind Prajapat
5
如果只需要最后一个数字，它被称为约瑟夫问题，有已知的公式可以在O(N)时间内计算出答案。
我不知道是否可以将其适应于运行完整模拟，因此我将在此描述一种直接的O(N log N)解决方案：
让我们将所有数字保存在具有隐式键的treap中。我们需要找到第k个元素并在每个步骤中删除它（实际上可能会有移位，所以更像是(cur_shift + k) % cur_size，但这并不重要）。 Treap可以做到这一点。我们只需要将其拆分为3部分[0，k-1]，[k，k]和[k + 1，cur_size-1]，在对应于第二部分的节点中打印数字，然后将第一部分和最后一部分合并。每步需要O(log N)时间，因此对于给定的限制应该足够好。
2
这里有一个二叉树的数组实现，仅将左子树的大小作为节点值存储。输入数组实际上并没有被存储，但假定它是二叉树底层以下的叶子节点。 

function josephusPermutation(size, step) {
    var len = 1 << 32 - Math.clz32(size-1), // Smallest power of 2 >= size
        tree = Array(len).fill(0), // Create tree in array representation 
        current = 0, 
        skip = step - 1,
        result = Array(size).fill(0),
        goRight, leftSize, order, i, j;

    // Initialise tree with sizes of left subtrees as node values
    (function init(i) {
        if (i >= len) return +(i - len < size); // Only count when within size
        var left = tree[i] = init(i*2); // recursive, only store left-size
        return left + (left ? init(i*2+1) : 0); // return sum of left and right 
    })(1);

    for (j = 0; j < result.length; j++, size--) {
        current = (current + skip) % size; // keep within range
        order = current;
        for (i = 1; i < len; i = i*2+goRight) {
            leftSize = tree[i];
            goRight = order >= leftSize;
            if (goRight) {
                order -= leftSize; // Moving rightward, counting what is at left side.
            } else {
                tree[i]--; // we will remove value at left side
            }
        }
        result[j] = 1 + i - len;
    }
    return result;
}

var sequence = josephusPermutation(100000, 123456);
console.log(sequence.join(','));

看你初始化树的方式，我意识到我的代码有时可能会高估节点左侧连接的数量。然而，如果一个节点在左侧有不完整的子树，则其右侧没有任何节点，因此您总是向左移动，而错误的计数无关紧要。我认为这也意味着您可以将树初始化为例如[7,3,3,1,1,1,1]，而无需使用递归计算节点数。 - m69 ''snarky and unwelcoming''
我认为这不适用于我构建的树。在10的情况下，该算法中的树具有8作为根计数值，而不是您结构所需的7。 - trincot
1
以下是王磊和王晓东（2013年）1的O(n log k)算法实现（非常类似于，如果不是基于1983年Errol Lloyd的算法）。其思想是将原始序列分成log k高度的n/m个二叉树。该算法实际上是为“猫科动物”约瑟夫问题设计的，其中参与者可以拥有多个生命（在下面的数组变量global.l中列出）。
我也喜欢Knuth，Ahrens和Kaplansky的O(1)空间算法（由Gregory Wilson，加州州立大学海沃德分校，1979年2在硕士论文中概述），虽然处理时间较长，但根据参数可以非常快速。
Knuth的J(n,d,t)（t是第ith次命中）递减序列的算法：
Let x1 = d * t and for k = 2,3,..., 
  let x_k = ⌊(d * x_(k−1) − d * n − 1) / (d − 1)⌋

Then J(n,d,t) = x_p where x_p is the first term in the sequence <= n.

Ahrens算法用于计算升序列J(n,d,t)：

Let a1 = 1 and for k = 2,3,... 
  let a_k = ⌈(n − t + a_(k−1)) * d / (d − 1)⌉ 
If a_r is the first term in the sequence such that a_r + 1 ≥ d * t + 1 
  then J(n,d,t) = d * t + 1 − a_r.

Kaplansky算法用于计算J(n,d,t)：

J(n,d,t)：

Let Z+ be the set of positive integers and for k =1,2,...,t 
  define a mapping P_k : Z+ → Z+ by P_k(m) = (m+d−1)−(n−k+1)(m−k+d−1)/(n−k+1)
Then, J(n,d,t) = P1 ◦ P2 ◦···◦Pt(t).

JavaScript代码：

var global = {
  n: 100000,
  k: 123456,
  l: new Array(5).fill(1),
  m: null,
  b: null,
  a: [],
  next: [],
  prev: [],
  i: 0,
  limit: 5,
  r: null,
  t: null
}

function init(params){
  global.m = Math.pow(2, Math.ceil(Math.log2(params.k)));
  params.b = Math.ceil(params.n / global.m);
      
  for (let i=0; i<params.b; i++){
    let s = i * global.m,
        t = (i + 1) * global.m,
        u = [];
        
    for (let j=0; j<global.m; j++)
      u[j] = 0;
      
    for (let j=s; j<=Math.min(t-1,params.n-1); j++)
      u[j-s] = -(j + 1);
      
    global.a[i] = [];
    build(u, global.a[i]);
    
    t = (i + 1) % params.b;
    
    params.next[i] = t;
    params.prev[t] = i;
  }
}

function build(u,v){
  function count(_v, i){
    if (global.m < i + 2){
      if (_v[i] < 0)
        return 1;
      else
        return 0;
        
    } else {
      _v[i] = count(_v, 2*i + 1);
      _v[i] = _v[i] + count(_v, 2*i + 2);
      return _v[i];
    }
  }
  
  for (let i=0; i<global.m; i++)
    v[global.m + i - 1] = u[i];
    
  count(v, 0);
}

function algorithmL(n, b){
  global.r = 0;
  global.t = b - 1;
      
  while (global.i < global.limit){
    tree(global, global);
    let j = leaf(global, global);
    hit(global.i,j,global,global);
    global.i = global.i + 1;
  }
}

function tree(params_r,params_t){
  if (params_t.t === global.next[params_t.t] && params_r.r < global.k){
    params_r.r = global.k + global.a[params_t.t][0] - 1 - (global.k - params_r.r - 1) % global.a[params_t.t][0];
  } else {
    while (params_r.r < global.k){
      params_t.t = global.next[params_t.t];
      params_r.r = params_r.r + global.a[params_t.t][0];
    }
  }
}

function size(t,j){
  if (global.a[t][j] < 0)
    return 1
  
  return global.a[t][j];
}

function leaf(params_r,params_t){
  let j = 0,
      nxt = params_r.r - global.k;
      
  while (j + 1 < global.m){
    let rs = size(params_t.t, 2*j + 2);
    if (params_r.r - rs < global.k){
      j = 2*j + 2;
    } else {
      j = 2*j + 1;
      params_r.r = params_r.r - rs;
    }
  }
  params_r.r = nxt;
  return j;
}

function hit(i,j,params_r,params_t){
  let h = -global.a[params_t.t][j];
  console.log(h);
  if (global.l[h-1] > 1)
    global.l[h-1] = global.l[h-1] - 1;
  else
    kill(i,j,params_r,params_t);
}

function kill(i,j,params_r,params_t){
  global.a[params_t.t][j] = 0;
  while (j > 0){
    j = Math.floor((j - 1) / 2);
    global.a[params_t.t][j] = global.a[params_t.t][j] - 1;
  }
  if (params_t.t !== global.next[params_t.t]){
    if (global.a[params_t.t][0] + global.a[global.next[params_t.t]][0] === global.m){
      params_r.r = params_r.r + global.a[global.next[params_t.t]][0];
      combine(params_t);
    } else if (global.a[params_t.t][0] + global.a[global.prev[params_t.t]][0] === global.m){
      t = global.prev[params_t.t];
      combine(params_t);
    }
  }
}

function combine(params_t){
  let x = global.next[params_t.t],
      i = 0,
      u = [];
  
  for (let j=0; j<global.m; j++)
    if (global.a[params_t.t][global.m + j - 1] < 0){
      u[i] = global.a[params_t.t][global.m + j - 1];
      i = i + 1;
    }
  for (let j=0; j<global.m; j++)
    if (global.a[x][global.m + j - 1] < 0){
      u[i] = global.a[x][global.m + j - 1];
      i = i + 1;
    }
  build(u,global.a[params_t.t]);
  global.next[params_t.t] = global.next[global.next[params_t.t]];
  global.prev[global.next[params_t.t]] = params_t.t;
}

init(global);
algorithmL(global.n, global.b);

(1) L. Wang 和 X. Wang。广义 Josephus 问题算法的比较研究。《应用数学和信息科学》, 2013, 7(4): 1451-1457。

(2) Wilson（1979）的参考文献：

Knuth, D. E.，《计算机程序设计艺术》，Addison-Wesley，Reading Mass.，Vol I Fundamental Algorithms，1968，Ex. 22，p158；Vol. III，Sorting and Searching，Ex. 2，pp. 18-19；Vol. I，2nd ed.，p.181。

Ahrens, W.，《Mathematische Unterhaltungen und Spiele》，Teubner: Leipzig，1901，Chapter 15，286-301。

Kaplansky, I. 和 Herstein I.N.，《Matters Mathematical》，Chelsea，New York，1978，pp. 121-128。

网页内容由stack overflow 提供, 点击上面的
可以查看英文原文，
原文链接