每个k=1..n的子数组大小最大和

Question

对于一个大小为n的数组，对于每个k从1到n，找出大小为k的连续子数组的最大和。

这个问题有一个明显的解决方案，时间复杂度为O(N²)，空间复杂度为O(1)。Lua代码:

array = {7, 1, 3, 1, 4, 5, 1, 3, 6}
n = #array

function maxArray(k)
    ksum = 0
    for i = 1, k do
        ksum = ksum + array[i]
    end
    max_ksum = ksum
    for i = k + 1, n do
        add_index = i
        sub_index = i - k
        ksum = ksum + array[add_index] - array[sub_index]
        max_ksum = math.max(ksum, max_ksum)
    end
    return max_ksum
end

for k = 1, n do
    print(k, maxArray(k))
end

是否有时间复杂度更低的算法？例如，O(N log N) + 额外的内存。

相关主题：

• 卡兰尼算法

- starius

Answer 1

一种高效的解决方案是基于以下事实：可以使用之前大小为 k 的子数组（或窗口）的和来在 O(1) 时间内获得大小为 k 的子数组（或窗口）的总和。除了第一个大小为 k 的子数组外，对于其他子数组，我们通过删除上一个窗口的第一个元素并添加当前窗口的最后一个元素来计算总和。

下面是相同解决方案的实现代码：

int maxSum(int arr[], int n, int k) 
{ 
// k must be greater 
if (n < k) 
{ 
   cout << "Invalid"; 
   return -1; 
} 

// Compute sum of first window of size k 
int res = 0; 
for (int i=0; i<k; i++) 
   res += arr[i]; 

// Compute sums of remaining windows by 
// removing first element of previous 
// window and adding last element of  
// current window. 
int curr_sum = res; 
for (int i=k; i<n; i++) 
{ 
   curr_sum += arr[i] - arr[i-k]; 
   res = max(res, curr_sum); 
} 

return res; 
 } 

时间复杂度：O（n） 辅助空间：O（1）

来源：Source

- Srinath gunnu

Answer 2

这个问题可以简化为最小和卷积，参见第2.4节（MCSP）在https://core.ac.uk/download/pdf/84869149.pdf中。因此，目前您可以期望的最佳复杂度可能是O（n^2 / polylog（n））。

- newbie

Answer 3

如果没有添加其他约束条件，我不认为有比O(N²)更高效的解决方案。换句话说，没有其他方法来确定您已经找到了最大和子数组，而不是探索所有其他子数组。

因此，最简单的解决方案包括O(N²/2)，即给定长度N的数组的所有连续子数组的总数。

个人而言，我会使用动态规划方法来实现这一点。思路是拥有一组部分结果，然后使用它们来构建子数组的当前和（代替计算整个总和）。无论如何，这只会给出“恒定”的加速，因此复杂度为O(N²/2)~O(N²)。

以下是伪代码-很抱歉我不会用Lua

// here we place temporary results, row by row alternating in 0 or 1
int[2][N] sum_array_buffer
// stores the start of the max subarray
int[N] max_subarray_start
// stores the value
int[N] max_subarray_value

array = {7, 1, 3, 1, 4, 5, 1, 3, 6}
// we initialize the buffer with the array (ideally 1-length subarrays)
sum_array_buffer[1] = array
// the length of subarrays - we can also start from 1 if considered
for k = 1 ; k <= (N); ++k:
    // the starting position fo the sub-array
    for j = 0; j < (N-k+1); ++j:
        sum_array_buffer[k%2][j] = sum_array_buffer[(k+1)%2][j] + array[j+k-1]
        if j == 0 || sum_array_buffer[k%2][j] > max_subarray_value[k]:
            max_subarray_value = sum_array_buffer[k%2][j]
            max_subarray_start[k] = j


for k = 1 ; k <= (N); ++k:
    print(k, max_subarray_value[k])

图形化地：

- Fabio Veronese

Answer 4

我们创建一个名为Qi的Dequeue，其容量为k，仅存储当前k个元素窗口中的有用元素。如果元素在当前窗口中并且大于其左侧当前窗口中所有其他元素，则该元素是有用的。我们逐个处理所有数组元素，并维护Qi以包含当前窗口的有用元素，并以排序顺序维护这些有用元素。 Qi前面的元素是最大的元素，而Qi后面的元素是当前窗口中最小的元素。

- user5811614

Answer 5

int maxCrossingSum(int arr[], int l, int m, int h) 
{ 
    // Include elements on left of mid. 
    int sum = 0; 
    int left_sum = INT_MIN; 
    for (int i = m; i >= l; i--) 
    { 
        sum = sum + arr[i]; 
        if (sum > left_sum) 
          left_sum = sum; 
    } 

    // Include elements on right of mid 
    sum = 0; 
    int right_sum = INT_MIN; 
    for (int i = m+1; i <= h; i++) 
    { 
        sum = sum + arr[i]; 
        if (sum > right_sum) 
          right_sum = sum; 
    } 

    // Return sum of elements on left and right of mid 
    return left_sum + right_sum; 
} 

// Returns sum of maxium sum subarray in aa[l..h] 
int maxSubArraySum(int arr[], int l, int h) 
{ 
   // Base Case: Only one element 
   if (l == h) 
     return arr[l]; 

   // Find middle point 
   int m = (l + h)/2; 

   /* Return maximum of following three possible cases 
      a) Maximum subarray sum in left half 
      b) Maximum subarray sum in right half 
      c) Maximum subarray sum such that the subarray crosses the midpoint */
   return max(maxSubArraySum(arr, l, m), 
              maxSubArraySum(arr, m+1, h), 
              maxCrossingSum(arr, l, m, h)); 
} 

解释

使用分治法，我们可以在O(nLogn)时间内找到最大子数组和。以下是分治算法。

1）将给定的数组分成两半

2）返回以下三个中的最大值

….a）左半部分的最大子数组和（进行递归调用）

….b）右半部分的最大子数组和（进行递归调用）

---

源代码

- Anshuman Kumar

Answer 6

    The above question can be solved by O(n).
    Please try this algorithm.
    lets say k=3.
array = {7, 1, 3, 1, 4, 5, 1, 3, 6}
    maxsum=0.
    1)We start with adding 7+1+3 and store sum=11.since sum >maxsum.maxsum=11.
    2)Now since size of k=3,next continuous array is 1+3+1.so how we get this sum??
    remove 7 from sum and add 1 to sum.so now sum is 5.Check if sum>maxsum.
    3)Similarly do for other elements as well.This loop will run until (n-1).``

请在此处找到代码。

 class Program
    {
        static void Main(string[] args)
        {
            int sum=0;
            int max=0;
            int size=9;
           string input="7, 1, 3, 1, 4, 5, 1, 3, 6";
           string[] values=input.Split(',');
           int length=values.Length;
           int k=size-1;
           for(int i=0;i<=k;i++)
           {
             sum=sum+int.Parse(values[i]);
             max=sum;
           }
           for(int j=0;k<length-1;j++)
           {
               ++k;
            sum=(sum-int.Parse(values[j]))+int.Parse(values[k]);
            if(sum>max)
            max=sum;
           }
           Console.WriteLine(max);
        }
    }

- CodeOfLife

Answer 7

以下过程可能会对您有所帮助

1）选择第一组k个元素，并创建一个大小为k的自平衡二叉搜索树(BST)。

2）运行循环，从i=0到n-k：

…..a）从BST中获取最大元素并打印出来。

…..b）在BST中查找arr[i]并将其从BST中删除。

…..c）将arr[i+k]插入到BST中。

时间复杂性：步骤1的时间复杂度为O(kLogk)。步骤2(a)，2(b)和2(c)的时间复杂度为O(Logk)。由于步骤2(a)，2(b)和2(c)循环运行n-k+1次，因此整个算法的时间复杂度为O(kLogk + (n-k+1)*Logk)，也可以写成O(nLogk)。

- Pavan Kumar K

---

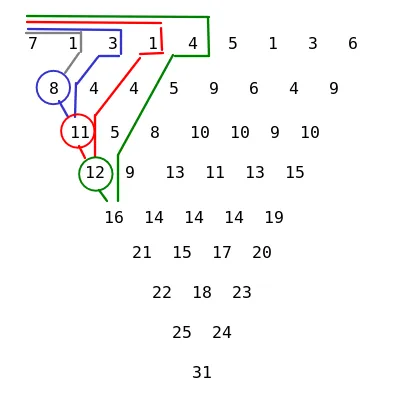
当对于每个 k=1,....,n 进行操作时，其时间复杂度为 O(n^2logn)。这种方法比 OP 的解决方案更低效。使用滑动窗口可以在 O(n) 的时间内找到 k 个相邻元素的最大和。因此，不需要使用 O(nlogk) 的树解决方案。 - amit

我可以在 O(N) 的时间内解决给定k的子问题。这个问题的关键点是需要找到每个 k 从 1 到 n 对应的最大和的 k-子数组。 - starius