斐波那契堆数据结构的名称中包含“斐波那契”一词，但数据结构中似乎没有使用斐波那契数。根据维基百科文章：
斐波那契堆的名称来自斐波那契数，在运行时间分析中使用。
这些斐波那契数是如何在斐波那契堆中出现的？
2个回答
23
斐波那契堆由一组不同“顺序”的较小堆有序树构成，遵守某些结构约束条件。斐波那契数列的出现是因为这些树以一种方式构建，使得一个顺序为n的树中至少有Fn+2个节点，其中Fn+2是第(n+2)个斐波那契数。
要看到为什么这个结果是正确的，让我们从了解斐波那契堆中的树是如何构建的开始。最初，每当将节点放入斐波那契堆时，它都会被放入一个顺序为0的树中，该树只包含该节点。每当从斐波那契堆中删除值时，一些斐波那契堆中的树会合并在一起，以使树的数量不会变得太大。
在合并树时，斐波那契堆仅合并相同顺序的树。要将两棵顺序为n的树合并成一棵顺序为n + 1的树，斐波那契堆会选择具有比另一棵更大的根值的树，然后将该树作为另一棵树的子节点。这个事实的一个结果是，顺序为n的树总是恰好有n个子节点。
Fibonacci堆的主要吸引力在于它支持高效地降低键值（摊销O（1））。为了支持此功能，Fibonacci堆将降低键值实现如下：要降低存储在某个节点中的值的键，该节点从其父树中切断并视为自己单独的树。当发生这种情况时，其旧父节点的顺序减少了一个。例如，如果一个顺序为4的树有一个被切掉的子节点，则它会缩小为一个顺序为3的树，这是有意义的，因为树的顺序应该是它包含的子节点数。
这样做的问题在于，如果从同一棵树上切掉太多的树，我们可能会得到一棵具有很大顺序但包含非常少节点的树。如果具有大顺序的树只包含少量节点，那么Fibonacci堆的时间保证只有在包含大量节点的大顺序树中才能实现，如果我们可以随意切割任何节点，我们很容易陷入一个情况，即具有巨大顺序的树仅包含少量节点。
为了解决这个问题，Fibonacci堆提出了一个要求 - 如果您从一棵树中切掉两个子节点，则必须依次从其父树中切掉该树。这意味着形成Fibonacci堆的树不会因降低键值而受到太大的损害。
现在我们可以谈谈斐波那契数列的部分。此时，我们可以说以下关于斐波那契堆中树的内容：
让我们试试一些例子。只有一个可能的0阶树，它只是一个单独的节点：
现在我们可以发现一个模式。最小可能的(n + 2)阶树将如下形成：首先创建一个正常的(n + 2)阶树，它有n + 1，n，n - 1，...，2，1，0阶的子节点。然后，通过从中删除节点而不切断同一节点的两个子节点来尽可能缩小这些树。这将留下一个具有n、n - 2、...、1、0和0阶子节点的树。
现在我们可以编写一个递归关系来确定这些树中有多少个节点。如果我们这样做，我们得到以下结果，其中NC(n)表示可能存在的n阶树中最小的节点数：
在这里，最后的+1是为了计算根节点本身。
如果我们展开这些术语，我们得到以下内容：
如果您注意到的话，这正是斐波那契数列偏移了两个位置。换句话说，每棵树都必须至少有Fn+2个节点，其中Fn + 2是第（n + 2）个斐波那契数。
那么为什么它被称为斐波那契堆呢？因为每个顺序为n的树都必须至少有Fn+2个节点！
如果您好奇，斐波那契堆的原始论文上有这些最小可能的树的图片。看起来很不错！此外，查看这篇CS理论Stack Exchange帖子，了解关于为什么斐波那契堆树具有其大小的替代解释。
希望这可以帮到您！
要看到为什么这个结果是正确的，让我们从了解斐波那契堆中的树是如何构建的开始。最初，每当将节点放入斐波那契堆时，它都会被放入一个顺序为0的树中，该树只包含该节点。每当从斐波那契堆中删除值时，一些斐波那契堆中的树会合并在一起，以使树的数量不会变得太大。
在合并树时，斐波那契堆仅合并相同顺序的树。要将两棵顺序为n的树合并成一棵顺序为n + 1的树，斐波那契堆会选择具有比另一棵更大的根值的树，然后将该树作为另一棵树的子节点。这个事实的一个结果是，顺序为n的树总是恰好有n个子节点。
Fibonacci堆的主要吸引力在于它支持高效地降低键值（摊销O（1））。为了支持此功能，Fibonacci堆将降低键值实现如下：要降低存储在某个节点中的值的键，该节点从其父树中切断并视为自己单独的树。当发生这种情况时，其旧父节点的顺序减少了一个。例如，如果一个顺序为4的树有一个被切掉的子节点，则它会缩小为一个顺序为3的树，这是有意义的，因为树的顺序应该是它包含的子节点数。
这样做的问题在于，如果从同一棵树上切掉太多的树，我们可能会得到一棵具有很大顺序但包含非常少节点的树。如果具有大顺序的树只包含少量节点，那么Fibonacci堆的时间保证只有在包含大量节点的大顺序树中才能实现，如果我们可以随意切割任何节点，我们很容易陷入一个情况，即具有巨大顺序的树仅包含少量节点。
为了解决这个问题，Fibonacci堆提出了一个要求 - 如果您从一棵树中切掉两个子节点，则必须依次从其父树中切掉该树。这意味着形成Fibonacci堆的树不会因降低键值而受到太大的损害。
现在我们可以谈谈斐波那契数列的部分。此时，我们可以说以下关于斐波那契堆中树的内容：
- 一个n阶树恰好有n个子节点。
- n阶树是通过取两个n-1阶树并将其中一个作为另一个的子节点来形成的。
- 如果一棵树失去了两个子节点，则该树将从其父节点中切断。
让我们试试一些例子。只有一个可能的0阶树，它只是一个单独的节点：
Smallest possible order 0 tree: *
最小可能的一阶树至少需要一个带有子节点的节点。我们能够创建的最小可能的子节点是一个只有一个子树为最小零阶树的单个节点，该树如下所示：
Smallest possible order 1 tree: *
|
*
那么二阶最小的树是什么样子呢？这就变得有趣了。这棵树肯定要有两个子节点，它将由两棵一阶树合并而成。因此，这棵树最初会有两个子节点——一棵零阶树和一棵一阶树。但请记住——我们可以在合并树后从中切除子节点！在这种情况下，如果我们切除一阶树的子节点，我们将得到一棵有两个子节点的树，它们都是零阶树：
Smallest possible order 2 tree: *
/ \
* *
那么3阶的情况呢？和之前一样，这个树是由两个2阶树合并而成的。然后我们会尽可能地剪掉这个3阶树的子树。当它被创建时，它有2、1、0阶的子树。我们无法从0阶子树中剪切，但可以从2阶和1阶子树中各剪切一个子节点。这样，我们就得到了一个具有三个子节点的树，其中一个是1阶，另外两个是2阶：
Smallest possible order 3 tree: *
/|\
* * *
|
*
现在我们可以发现一个模式。最小可能的(n + 2)阶树将如下形成：首先创建一个正常的(n + 2)阶树，它有n + 1，n，n - 1，...，2，1，0阶的子节点。然后，通过从中删除节点而不切断同一节点的两个子节点来尽可能缩小这些树。这将留下一个具有n、n - 2、...、1、0和0阶子节点的树。
现在我们可以编写一个递归关系来确定这些树中有多少个节点。如果我们这样做，我们得到以下结果，其中NC(n)表示可能存在的n阶树中最小的节点数：
NC(0) = 1
NC(1) = 2
NC(n + 2) = NC(n) + NC(n - 1) + ... + NC(1) + NC(0) + NC(0) + 1
在这里，最后的+1是为了计算根节点本身。
如果我们展开这些术语，我们得到以下内容：
NC(0) = 1
NC(1) = 2
NC(2) = NC(0) + NC(0) + 1 = 3
NC(3) = NC(1) + NC(0) + NC(0) + 1 = 5
NC(4) = NC(2) + NC(1) + NC(0) + NC(0) + 1 = 8
如果您注意到的话，这正是斐波那契数列偏移了两个位置。换句话说，每棵树都必须至少有Fn+2个节点，其中Fn + 2是第（n + 2）个斐波那契数。
那么为什么它被称为斐波那契堆呢？因为每个顺序为n的树都必须至少有Fn+2个节点！
如果您好奇，斐波那契堆的原始论文上有这些最小可能的树的图片。看起来很不错！此外，查看这篇CS理论Stack Exchange帖子，了解关于为什么斐波那契堆树具有其大小的替代解释。
希望这可以帮到您！
- templatetypedef
4
我猜问题在于我们不知道树的大小，只能通过它们的等级来近似表示。如果我们能知道大小，就可以像哈夫曼编码一样合并它们，而不需要删除父节点。然而，跟踪树的大小太昂贵了。 - Thomas Ahle
@ThomasAhle 没错。斐波那契堆被优化为允许摊销O(1)的减少键值，通过从其父节点中剪切节点并仅更新直接父节点中的信息。如果您从其父节点中剪切一个节点，则必须在其所有祖先上更新子树大小，但这需要时间Ω(log n)，并且会破坏O(1)减少键值的时间限制。 - templatetypedef
我想知道是否有人尝试过存储树大小的随机近似值。然后，当删除一个子节点时，算法会以'1、1/2、1/4...'的概率减少其祖先的大小，有点像跳表。实际上，这可能既不比已经存在的其他堆更简单也不更快。 - Thomas Ahle
@ThomasAhle 我认为这个存在，并且在期望上具有与斐波那契堆相同的保证。 - templatetypedef
5
我想给出一个直观的解释，让人们也能像我一样有“啊哈！”的时刻。树结构实现O(log n)的运行时间，因为它们能够按其高度存储指数级数量的项。二叉树可以存储2^h个，三叉树可以存储3^h个，通用情况下可存储x^h个。x可以小于2吗？当然可以！只要x>1，我们仍然可以实现对数运行时间，并且能够存储指数级大量的项。但是我们如何构建这样的树呢？斐波那契堆是一种数据结构，其中x≈1.62，或者说是黄金比例。每当我们遇到黄金比例时，都会有斐波那契数隐藏在某处...... 斐波那契堆实际上是一片树林。经过称为“合并”的过程后，每个树都包含不同数量的项，这些项是2的幂次方。例如，如果你的斐波那契堆有15个项，它将有4棵树，分别持有1、2、4和8个项，看起来像这样：
我们允许每个父节点失去多达一个子节点。如果随后尝试从同一父节点中删除另一个子节点，则我们还将将该父节点从该树中剪切出来，并将其放入根列表作为1个树。
上述规则确保树即使在最坏情况下仍具有指数项高度。什么是最坏情况？最坏情况发生在我们使每个父节点失去一个子节点时。如果父节点有>1个子节点，我们可以选择哪个子节点进行处理。在这种情况下，让我们摆脱具有最大子树的子节点。因此，在上图中，如果您对每个父节点都这样做，您将得到大小为1、1、2和3的树。看到模式了吗？只是为了好玩，在上面的图中添加新的4阶树（即16项），并猜测在对每个父节点运行此规则后会剩下什么：5。我们有一个斐波那契数列！
由于斐波那契序列是指数级的，每个树仍然保留指数数量的项，因此可以在EXTRACT-MIN操作中具有O(log n)运行时间。但请注意，DECREASE-KEY现在只需要O(1)。另一个很酷的事情是，您可以将任何数字表示为斐波那契数的总和。例如，32 = 21 + 8 + 3，这意味着如果您需要在斐波那契堆中保存32个项目，则可以使用三棵树分别保存21、8和3个项目。但是，“合并”过程不会产生节点数为斐波那契数的树。它们只在发生DECREASE-KEY或DELETE的最坏情况下出现。 进一步阅读
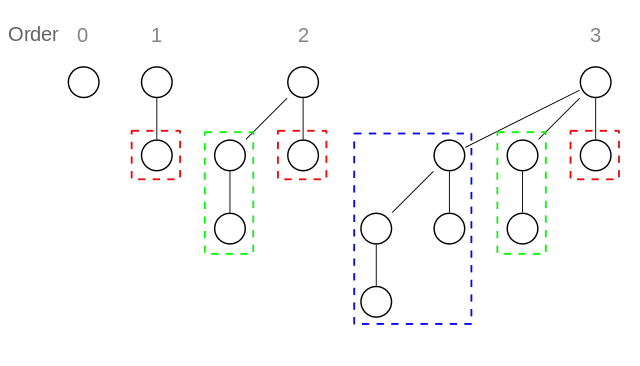
"合并"过程的细节并不重要，但本质上它基本上是将同一度数的树联合在一起，直到所有树都具有不同的度数（尝试使用酷炫的可视化工具来查看这些树是如何构建的）。由于您可以将任何n写成2的确切幂的和，因此很容易想象对于任何n，Fibonacci堆的合并树会是什么样子。
到目前为止，我们仍然没有看到斐波那契数列的直接联系。它们实际上出现在非常特殊的情况下，这也是为什么斐波那契堆可以为DECREASE-KEY操作提供O(1)时间的关键所在。当我们减少一个键时，如果新键仍然大于父键，则我们不需要做任何其他事情，因为最小堆属性没有被违反。但如果不是这样，我们不能让较小的子节点埋藏在更大的父节点下面，因此我们需要将其子树剪切出来，并将其制作成新树。显然，我们不能每次删除都这样做，否则我们最终会得到树太高且不再具有指数项的树，这意味着提取操作不再具有O(log n)时间。所以问题是我们可以设置什么规则，使树仍然具有指数项的高度？聪明的想法是这样的：我们允许每个父节点失去多达一个子节点。如果随后尝试从同一父节点中删除另一个子节点，则我们还将将该父节点从该树中剪切出来，并将其放入根列表作为1个树。
上述规则确保树即使在最坏情况下仍具有指数项高度。什么是最坏情况？最坏情况发生在我们使每个父节点失去一个子节点时。如果父节点有>1个子节点，我们可以选择哪个子节点进行处理。在这种情况下，让我们摆脱具有最大子树的子节点。因此，在上图中，如果您对每个父节点都这样做，您将得到大小为1、1、2和3的树。看到模式了吗？只是为了好玩，在上面的图中添加新的4阶树（即16项），并猜测在对每个父节点运行此规则后会剩下什么：5。我们有一个斐波那契数列！
由于斐波那契序列是指数级的，每个树仍然保留指数数量的项，因此可以在EXTRACT-MIN操作中具有O(log n)运行时间。但请注意，DECREASE-KEY现在只需要O(1)。另一个很酷的事情是，您可以将任何数字表示为斐波那契数的总和。例如，32 = 21 + 8 + 3，这意味着如果您需要在斐波那契堆中保存32个项目，则可以使用三棵树分别保存21、8和3个项目。但是，“合并”过程不会产生节点数为斐波那契数的树。它们只在发生DECREASE-KEY或DELETE的最坏情况下出现。 进一步阅读
- 二项堆 - 斐波那契堆本质上是一种懒惰的二项堆。这是一种很酷的数据结构，因为它展示了一种在树的高度上存储指数项的不同方式，而不是二叉堆。
- 斐波那契堆背后的直觉 - 任何想要理解斐波那契堆核心思想的人都需要阅读此内容。教科书对此主题通常过于肤浅和杂乱无章，但是这个SO答案的作者完美地解决了这个问题。
- Shital Shah
网页内容由stack overflow 提供, 点击上面的可以查看英文原文，
原文链接
原文链接