Product和Coproduct：
余积：
据我了解，在Haskell中，Product类型举例来说是：data Pair = P Int Double
一个Sum类型是：
data Pair = I Int | D Double
如何理解与Sum和Product类型相关的图像？
这些图片来自http://blog.higher-order.com/blog/2014/03/19/monoid-morphisms-products-coproducts/。
A，B和Zf和g（在第一个图中，f :: Z -> A，g :: Z -> B，在第二个图中箭头会“反过来”，因此f :: A -> Z和g :: B -> Z）。现在我将集中讨论第一个图，这样我就不必用稍微有些变化的方式说两遍了。
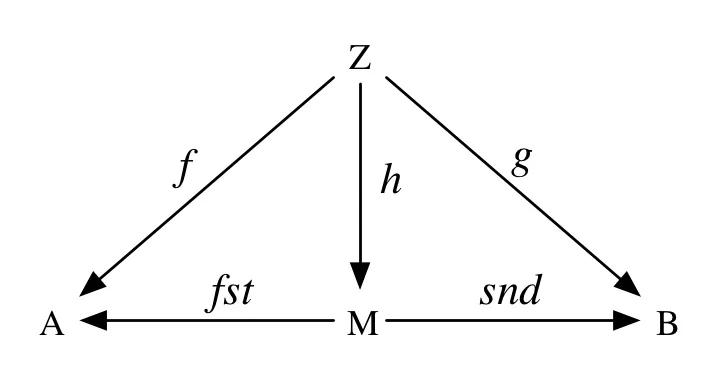
无论如何，根据以上内容，想法就是有一种类型M以及函数fst :: M -> A，snd :: M -> B和h :: Z -> M，使得，正如数学家所说的那样，图表“交换”。这只是表示，在给定图表中的任意两点上，如果您按任何方式从其中一个点沿着箭头走到另一个点，结果的函数都是相同的。即，f与fst . h相同，而g与snd . h相同。
很容易看出，无论Z是什么，都可以使用配对类型(A, B)及通常的Haskell函数fst和snd实现这一点——再加上适当的h选择，即：
h z = (f z, g z)
这两个要求在图表中形成交换所必须满足的特定条件，是很容易得到满足的。
这是有关图表的基本解释。但您可能会对其中Z的角色略感困惑。这是因为实际上陈述的是相当强的内容。也就是说，给定A、B、f和g，存在一个M以及函数fst和snd，可以为任何类型Z（这意味着还需要提供一个函数h::Z->M）构造出这样的图表。并且进一步说明只有一种函数h能够满足所需的属性。
一旦您玩弄它并理解各种要求，就很清楚了，配对(A,B)以及其他与之同构的类型（基本上意味着定义了data MyPair a b = MyPair a b的MyPair A B）是唯一满足此条件的东西。而且还有其他类型的M也可以起作用，但会产生不同的h，例如：将M作为三元组(A, B, Int)，其中fst和snd分别从第一个和第二个组件提取（在数学术语中称为“投影”），然后对于任何您要命名的x :: Int，h z = (f z, g z, x)都是这样的一个函数。
距我学习数学，特别是范畴论已经太长时间了，无法证明(A,B)是唯一满足我们所讨论的“通用性质”的类型。但可以放心地说它确实是唯一的，而且您真的不需要理解这个（或者实际上任何内容）才能在Haskell中使用积类型和和类型。
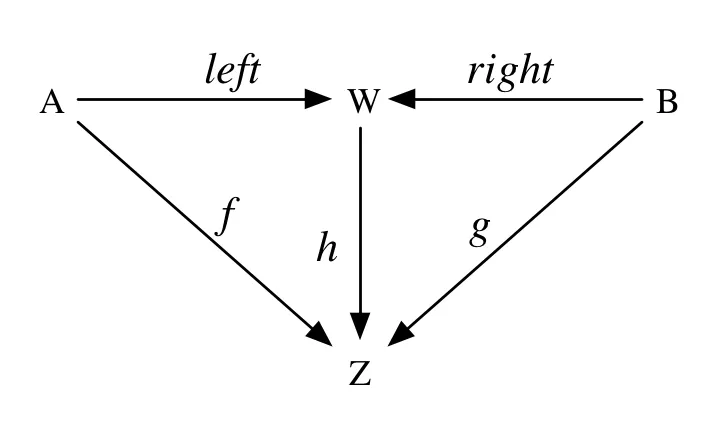
第二个图表与第一个图表基本相同，只是所有箭头都被反转了。在这种情况下，A和B的“余积”或“和”M实际上是Either a b（或其等价物），并且定义为：h::M->Z将被定义为：
h (Left a) = f a
h (Right b) = g b
a and B=b.I must produce an object (type) and two arrows (functions). I pick M=Pair a b. Then I must write functions of type Pair a b -> a (for the arrow fst : M -> A) and Pair a b -> b (for the arrow snd : M -> B). I choose:
fst :: Pair a b -> a
fst (P a b) = a
snd :: Pair a b -> b
snd (P a b) = b
z and two arrows (functions); f will have type z -> a and g will have type z -> b.I must produce a function h of type z -> Pair a b. I choose:
h = \z -> P (f z) (g z)
This h is required to make the diagram commute. This means that any two paths through the diagram that begin and end at the same object should be equal. For the diagrams given, that means we must show that it satisfies two equations:
f = fst . h
g = snd . h
I'll prove the first; the second is similar.
fst . h
= { definition of h }
fst . (\z -> P (f z) (g z))
= { definition of (.) }
\v -> fst ((\z -> P (f z) (g z)) v)
= { beta reduction }
\v -> fst (P (f v) (g v))
= { definition of fst }
\v -> f v
= { eta reduction }
f
As required.