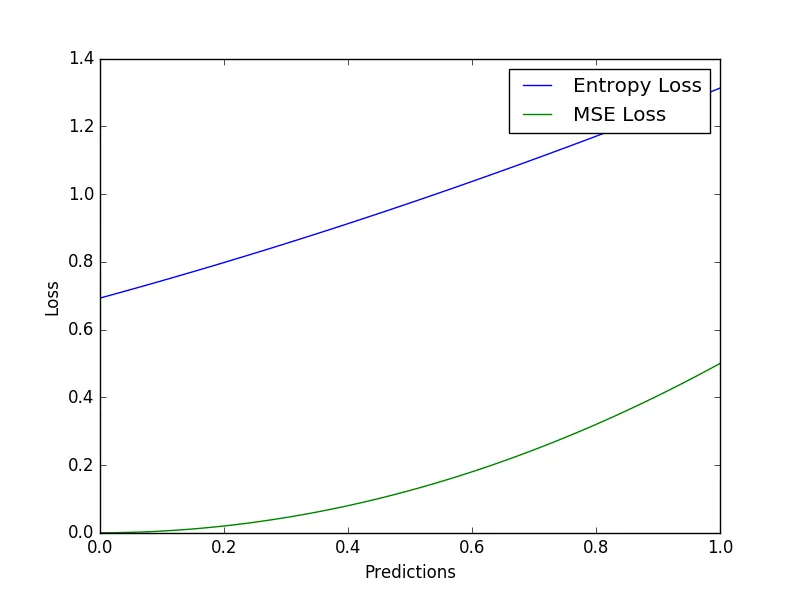
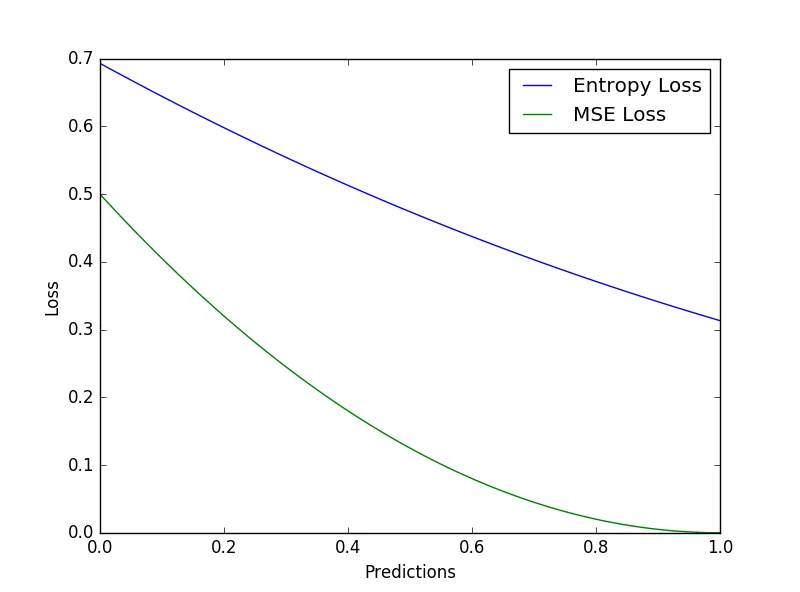
以收敛速度比较均方误差损失和交叉熵损失

Question

以收敛速度比较均方误差损失和交叉熵损失

machine-learninglogistic-regressionlosscross-entropymean-square-error

4

对于一个非常简单的分类问题，其中我有一个目标向量[0,0,0,....0]和一个预测向量[0,0.1,0.2,....1]，交叉熵损失更快/更好地收敛还是均方误差损失？当我绘制它们时，似乎MSE损失具有较低的误差边界。为什么会这样？

或者例如当我将目标设置为[1,1,1,1....1]时，我得到以下结果：

- aa1

我的回答关于MSE vs cross_entropy会很有帮助。 - vipin bansal

1

@vipinbansal 不幸的是，它不会。 - iRestMyCaseYourHonor

4个回答

8

你听起来有点困惑...

比较MSE和交叉熵损失的值并说其中一个比另一个低，就像是在比较苹果和橙子一样
MSE用于回归问题，而交叉熵损失用于分类问题；这些上下文是互相排斥的，因此比较它们对应的损失度量的数值是没有意义的
当你的预测向量是像[0,0.1,0.2,....1]这样的（即具有非整数分量）时，正如你所说，问题是一个回归问题（而不是分类问题）；在分类设置中，我们通常使用独热编码的目标向量，其中只有一个分量为1，其余都为0
[1,1,1,1....1]的目标向量可以是回归设置中的情况，也可以是多标签多类别分类的情况，即输出可能同时属于多个类别

除此之外，你选择的图表，水平轴上的百分比（？），令人困惑 - 我从未在ML诊断中看到过这样的图表，也不太确定它们到底代表什么或者为什么它们有用...

如果你想详细讨论分类设置中的交叉熵损失和准确性，可以看看我在这个答案中的内容。

- desertnaut

“MSE用于回归问题，而交叉熵损失用于分类问题……” 我经常听到这样的话，但我还没有找到一个好的解释为什么MSE不能/不应该用于分类问题。我能想到的唯一一件事是，对数函数比平方函数更陡峭，因此它会更好地惩罚错误预测，并在理论上导致更快的收敛。” - Super-intelligent Shade

@Super-intelligentShade 请查看自己的答案此处的最后一部分。 - desertnaut

谢谢您的回答，但是这个问题正好相反。我仍然看不出为什么均方误差不能应用于分类问题。 - Super-intelligent Shade

@Super-intelligentShade，我没有提到问题；我说的是 - 检查我的答案的最后一部分，在那里我部分地解决了这个问题（这与原始问题无关）。 - desertnaut

1

我最终找到了一个令人满意的答案，来自伟大的Andrew Ng本人：使用MSE与sigmoid激活相结合将导致非凸代价函数具有许多局部最优解。就这么简单。 - Super-intelligent Shade

1

针对你的第一个问题，简单回答如下：

对于一个非常简单的分类问题...使用交叉熵损失函数和均方误差损失函数哪个会更好/更快地收敛？

答案是，当与sigmoid激活结合使用时，MSE损失函数会导致多个局部最小值的非凸代价函数。这是由Andrew Ng教授在他的讲座中解释的：

Lecture 6.4 — Logistic Regression | Cost Function — [ Machine Learning | Andrew Ng]

我想同样适用于softmax激活的多类别分类。

- Super-intelligent Shade

0

我倾向于不同意之前给出的答案。关键在于交叉熵和均方误差损失是相同的。

现代神经网络使用参数空间的最大似然估计（MLE）来学习其参数。最大似然估计器由参数空间上概率分布的乘积的argmax给出。如果我们应用对数变换并通过自由参数的数量缩放MLE，我们将获得由训练数据定义的经验分布的期望。

此外，我们可以假设不同的先验条件，例如高斯或Bernoulli，它们分别产生MSE损失或Sigmoid函数的负对数似然。

更多阅读资料: Ian Goodfellow的《深度学习》

- polkadot21

网页内容由stack overflow 提供, 点击上面的

可以查看英文原文，
原文链接

- Mitiku · Accepted Answer

作为对被接受的答案的补充，我将回答以下问题：

从概率角度来看，MSE损失和交叉熵损失的解释是什么？
为什么分类使用交叉熵，线性回归使用MSE？

TL;DR 如果（随机）目标变量来自高斯分布，则使用MSE损失；如果（随机）目标变量来自多项式分布，则使用分类交叉熵损失。

MSE（均方误差）

线性回归的假设之一是多变量正态性。由此可以得出目标变量服从正态分布的结论（关于线性回归的假设更多信息可在这里和这里找到）。

高斯分布（正态分布）的均值为 $\mu$ ，方差为 $\sigma^2$ ，表示为
$\mathcal{N}(x|\mu,\sigma^2)=\frac{1}{\sqrt{2\pi\sigma^{2}}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$
在机器学习中，我们经常处理均值为0，方差为1的分布（或将数据转换为具有均值为0和方差为1）。此时正态分布为
$\mathcal{N}(x|\mu=0,\sigma^2=1)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}$ ，称为标准正态分布。
对于具有权重参数 $\mathbf{w}$ 和精度（逆方差）参数 $\beta$ 的正态分布模型，给定输入 $\mathbf{x}$ ，观察到单个目标t的概率由以下方程表示：

$\mathcal{p(t|x,\mathbf{w},\beta)=\mathcal{N}(t|y(x,\mathbf{w}),\beta^{-1})$ ，其中 $y(x,\mathbf{w})$ 是分布的均值，由模型计算得出：

$y(x,\mathbf{w})=\sum_{i=1}^{m}w_ix^i$

现在，给定输入 $\mathbf{X}$ ，目标向量 $\mathbf{t}$ 的概率可以表示为：

$p(\mathbf{t}|\mathbf{X},\mathbf{w},\beta)=\prod_{n=1}^{N}\mathcal{N}(t_n|y(x_n,\mathbf{w}),\beta^{-1})=$ $\prod_{n=1}^{N}\frac{\beta}{\sqrt{2\pi}}e^{-\beta\frac{(t_n-y(x_n,w))^2}{2}}$
取左右两边的自然对数可得：

$\ln p(\mathbf{t}|\mathbf{X},\mathbf{w},\beta)=\ln \prod_{n=1}^{N}\frac{\beta}{\sqrt{2\pi}}e^{-\beta\frac{(t_n-y(x_n,w))^2}{2}}$
$=-\frac{\beta}{2}\sum_{n=1}^N\left{y(x_n,w)-t_n\right}^2+\frac{N}{2}\ln\beta-\frac{N}{2}\ln(2\pi)=$ $\ln L(\mathbf{w},\beta}|\mathbf{X},\mathbf{t})$
其中 $\ln L(\mathbf{w},\beta}|\mathbf{X},\mathbf{t})$ 是正态函数的对数似然，通常训练模型涉及相对于参数 $\mathbf{w}$ 最大化似然函数。现在参数 $\mathbf{w}$ 的最大似然函数为 (关于常数项的 $\mathbf{w}$ 可以省略)。

$\ln L(\mathbf{w},\beta}|\mathbf{X},\mathbf{t})=-\frac{\beta}{2}\sum_{n=1}^N\left{y(x_n,w)-t_n\right}^2$

训练模型时省略常数 $\frac{-\beta}{2}$ 不会影响收敛。

$\ln L(\mathbf{w},\beta}|\mathbf{X},\mathbf{t})=\sum_{n=1}^N\left{y(x_n,w)-t_n\right}^2$ 这被称为平方误差，取mean可得均方误差。
$\frac{1}{N}\ln L(\mathbf{w},\beta}|\mathbf{X},\mathbf{t})=\frac{1}{N}\sum_{n=1}^N\left{y(x_n,w)-t_n\right}^2$ ,

交叉熵

在深入了解更一般的交叉熵函数之前，我将解释特定类型的交叉熵 - 二元交叉熵。

二元交叉熵

二元交叉熵的假设是目标变量的概率分布来自伯努利分布。根据维基百科

伯努利分布是一个离散型随机变量的概率分布，它取值1的概率为 p，取值0的概率为 q=1-p

伯努利分布随机变量的概率为
$P(Y=k)=p^k(1-p)^{1-k}$ , 其中 $k\in\left{0,1\right}$ ，p 是成功的概率。这可以简单地写成 $P(y)=p^y(1-p)^{1-y}$
两边取负自然对数得到

$-\sum_{i=1}^{n}y_i\ln(p_i)$

这被称为二元交叉熵。涉及内容与编程有关。

分类交叉熵

交叉熵的泛化遵循随机变量是多元的（来自多项式分布）的一般情况，其概率分布如下：

$-\sum_{i=1}^{n}y_i\ln(p_i)$

$P(\mathbf{Y})=\prod_{n=1}^{N}p_n^{y_n}(1-p_n)^{1-y_n}={p_n}^{\sum_{n=1}^{N}y_n}(1-p_n)^{n-\sum_{n=1}^{N}y_n}}$

对两边取自然对数的负值，得到分类交叉熵损失。

$-\ln P(y)=-(\sum_{n=1}^{N}y_n\ln(p_n)+(1-y_n)\ln(1-p_n))$ ,