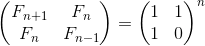以O(logn)的时间复杂度找到第n个斐波那契数。

Question

以O(logn)的时间复杂度找到第n个斐波那契数。

7

我正在试着解决这个问题: SPOJ problem。经过一些研究，我发现这其实可以归结为计算第n个斐波那契数的简单运算，但是n可能会非常大，所以O(n)解法并不好用。在Google上搜索后，我发现可以用O(logn)的时间复杂度计算第n个斐波那契数，而且还找到了一个完成该运算的代码示例：

long long fibonacci(int n) {
    long long fib[2][2] = {{1,1},{1,0}}, ret[2][2] = {{1,0},{0,1}}, tmp[2][2] = {{0,0},{0,0}};
    int i, j, k;
    while (n) {
        if (n & 1) {
            memset(tmp, 0, sizeof tmp);
            for (i = 0; i < 2; i++)
                for (j = 0; j < 2; j++)
                    for (k = 0; k < 2; k++)
                        tmp[i][j] = (tmp[i][j] + ret[i][k] * fib[k][j]);
            for (i = 0; i < 2; i++)
                for (j = 0; j < 2; j++)
                    ret[i][j] = tmp[i][j];
        }
        memset(tmp, 0, sizeof tmp);
        for (i = 0; i < 2; i++)
            for (j = 0; j < 2; j++)
                for (k = 0; k < 2; k++)
                    tmp[i][j] = (tmp[i][j] + fib[i][k] * fib[k][j]);
        for (i = 0; i < 2; i++)
            for (j = 0; j < 2; j++)
                fib[i][j] = tmp[i][j];
        n /= 2;
    }
    return (ret[0][1]);
}

我尝试修改了代码，但是仍然得到 WA 错误：http://ideone.com/3TtE5m

我是不是在计算模运算时出了错？还是有其他问题？

- user2947605

3

菲波那切数列还是质数？ - EvgeniyZh

对于SPOJ问题，请使用fib（n + 1），除非n = 0，我不确定0个硬币是否算作1种方式。请注意，（x％12345678901）* y（％12345678901）可能需要高达68位。在64位模式下，可以实现基于汇编的函数以对12345678901取模乘法，因为乘法后的积和除法前的被除数可以是128位。 - rcgldr

3个回答

5

斐波那契数列出现在

的连分数收敛项比值中，任何连分数的连分数收敛项所形成的矩阵行列式为+1或−1。

矩阵表示法为斐波那契数列提供了以下闭合形式表达式。

矩阵被乘以n次，因为只有这样我们才能得到结果矩阵中行和列(0,0)处的第(n+1)个斐波那契数作为元素。如果我们使用非递归矩阵乘法来应用上述方法，则时间复杂度为O(n)，空间复杂度为O(1)。但是，我们想要时间复杂度为O(log n)，因此我们必须优化上述方法，这可以通过递归乘以矩阵来完成获取第n次幂。上述规则的实现可以在下面找到。

#include <stdio.h>

void multiply(int F[2][2], int M[2][2]);

void power(int F[2][2], int n);

/*
The function that returns nth Fibonacci number.
*/

int fib(int n) {
    int F[2][2] = {{1, 1}, {1, 0}};
    if (n == 0)
        return 0;
    power(F, n - 1);
    return F[0][0];
}

/*
Optimized using recursive multiplication.
*/

void power(int F[2][2], int n) {
    if ( n == 0 || n == 1)
        return;
    int M[2][2] = {{1, 1}, {1, 0}};
    power(F, n / 2);
    multiply(F, F);
    if (n % 2 != 0)
        multiply(F, M);
}

void multiply(int F[2][2], int M[2][2]) {
    int x = F[0][0] * M[0][0] + F[0][1] * M[1][0];
    int y = F[0][0] * M[0][1] + F[0][1] * M[1][1];
    int z = F[1][0] * M[0][0] + F[1][1] * M[1][0];
    int w = F[1][0] * M[0][1] + F[1][1] * M[1][1];
    F[0][0] = x;
    F[0][1] = y;
    F[1][0] = z;
    F[1][1] = w;
}

int main() {
    printf("%d\n", fib(15));
    /*
    15th Fibonacci number is 610.
    */
    return 0;
}

- Rajiv Singh

3

有一个非常简单的算法，只使用整数：

long long fib(int n) {
    long long a, b, p, q;
    a = q = 1;
    b = p = 0;
    while (n > 0) {
        if (n % 2 == 0) {
            long long qq = q*q;
            q = 2*p*q + qq;
            p = p*p + qq;
            n /= 2;
        } else {
            long long aq = a*q;
            a = b*q + aq + a*p;
            b = b*p + aq;
            n -= 1;
        }
    }
    return b;
}

基于Lucas序列的特性完成。

- orlp

时间复杂度是多少？如果使用模算术，能否计算n=10^18的值？ - user2947605

@AleksXPO 你可以通过在每一步骤上取模来使它成为模块化。这应该能够在眨眼间计算出10^18 - 它只需要大约60次迭代。 - orlp

如果有人错过了我对原问题的评论，请注意，(x%12345678901) * y(%12345678901) 可能需要高达68位。 - rcgldr

@rcgldr 我在这里有一个针对64位乘法取模的优化实现：https://github.com/orlp/libop/blob/9063749f2b678df858433f502b7f9648e96f657b/bits/intrin.h#L119 - orlp

网页内容由stack overflow 提供, 点击上面的

可以查看英文原文，
原文链接

- cerkiewny · Accepted Answer

希望你是指第n个斐波那契数。

为了实现这一点，您需要使用斐波那契数的矩阵分解，在此处进行了描述。

基本思想是采用Donald E. Knuth的矩阵恒等式形式来计算斐波那契数，即：

而不是以传统的方式计算斐波那契数列，您将尝试找到矩阵的幂（k），其中k是给定的数字。

因此，这是通过k次矩阵乘法解决问题，但并不真正有帮助，因为我们可以用更简单的方法来完成它。

但是等等！我们可以优化矩阵乘法。我们可以先对其进行平方，然后再进行一半的乘法。我们可以继续这样做。因此，如果给定的数字是2^a，则我们可以在a步内完成它。通过不断平方矩阵来实现。

如果数字不是2的幂，则可以对数字进行二进制分解，看看是否将给定的平方矩阵纳入最终产品。

在您的情况下，在每次乘法之后，您还需要对每个矩阵元素应用模运算符123456。

希望我的解释有所帮助，如果没有，请参见链接以获得更清晰和更长的解释。

实际上，这个任务还有一个注意事项：由于要求您提供给定数字的某些斐波那契数模数，因此您还应证明取每个矩阵元素的余数不会改变结果。换句话说，如果我们乘以矩阵并取余数，我们实际上仍然得到斐波那契数的余数。但由于余数运算在加法和乘法中是可分配的，因此它确实产生了正确的结果。