为什么SymPy不能将(-x3)(2/3)简化为x**2？

Question

为什么SymPy不能将(-x3)(2/3)简化为x**2？

3

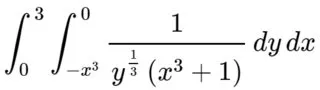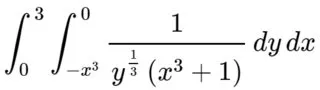我正试图使用SymPy计算以下积分： $\int_{lower}^{0}$ 手算时，答案为-½ log(28)。

我的工作与SymPy的结果一致，直到我对x进行积分。

x, y = sp.symbols('x y', real=True)
z = 1 / (sp.root(y, 3)*(x**3+1))
iz = z.integrate((y, -x**3, 0)) # integrate with respect to y
print(iz)
# -3*(-x**3)**(2/3)/(2*(x**3 + 1))
iiz = iz.integrate((x, 0, 3)) # integrate with respect to x
print(iiz)
# -3*Integral((-x**3)**(2/3)/(x**3 + 1), (x, 0, 3))/2
print(sp.N(iiz))
# 0.833051127543801 - 1.4428868782084*I

似乎SymPy无法处理(-x**3)**(2/3)。这应该简化为x**2，但SymPy不认为如此。手动简化产生了与我手动获取的相同答案。

print( sp.integrate(-3*x**2/(2*(x**3 + 1)), (x, 0, 3)) )
# -log(28)/2

有更好的方法来处理这个问题吗？

- nvi

我快速查看了https://docs.sympy.org/latest/tutorial/simplification.html#powers，其中列出了默认情况下未执行的简化操作，但不幸的是，它们都没有改变任何东西。你应该在github上进行查询https://github.com/sympy/sympy/issues。 - Aleksander Bobiński

abs() 匹配。 iiz 有一个 (-1)**(2/3) 项，这使得结果变成了复数。 - hpaulj

@hpaulj 关于 abs() 的观察真的很有趣。这是否意味着 -log(28)/2 和 0.833051127543801 - 1.4428868782084*I 都是有效答案，因为它们在复平面上距离原点的距离相同？ - nvi

@nvi：虽然−½ log(28) 和 0.83 − 1.44 i是正确的答案，但这并不是因为它们具有相同的绝对值（到原点的距离）。这只是来自特定方程的特殊属性所必需的属性。有许多满足该属性的数字，其中最多有三个解决方案（取决于您的方程式中^⅓的定义是什么，是否允许复杂的解决方案等等）。此外，对于其他问题，解可能具有不同的绝对值。 - Wrzlprmft

2个回答

1

在我的 isympy 会话中： SymPy 1.6.2

In [131]: z = 1 / (root(y,3)*(x**3+1))

In [132]: iz = z.integrate((y, -x**3, 0))

In [133]: iiz = iz.integrate((x,0,3))

In [134]: iiz
Out[134]: 
     2/3         
-(-1)   ⋅log(28) 
─────────────────
        2        

In [135]: N(iiz)
Out[135]: 0.833051127543801 - 1.4428868782084⋅ⅈ

In [136]: abs(iiz)
Out[136]: 
log(28)
───────
   2

root文档讨论返回主根，除了提供k参数外，建议使用real_root：

In [137]: z = 1 / (real_root(y,3)*(x**3+1))

In [138]: iz = z.integrate((y, -x**3, 0))

In [139]: iiz = iz.integrate((x,0,3))

In [140]: iiz
Out[140]: 
-log(28) 
─────────
    2    

In [141]: N(iiz)
Out[141]: -1.66610225508760

显然，双重积分有多个解，取决于根号的值。看起来它们都有相同的大小。听起来很合理，但我的复杂数学研究已经是很久以前的事情了，所以我不能提供理论上的证明。

当 k=2 时，我们得到第三个解：

In [146]: z = 1 / (root(y,3,2)*(x**3+1))

In [147]: iz = z.integrate((y, -x**3, 0))

In [148]: iiz = iz.integrate((x,0,3))

    In [149]: iiz
    Out[149]: 
    3 ____        
    ╲╱ -1 ⋅log(28)
    ──────────────
          2

因此，在复平面上有3个解，其乘法因子为-1, (-1)**(1/3), -(-1)**(2/3)，并且具有相同的大小。

-1.66610225508760
0.833051127543801 - 1.4428868782084⋅ⅈ
0.833051127543801 + 1.4428868782084⋅ⅈ

如果我们将一个整数符号k引入到z中：

In [158]: z = 1 / (root(y,3,k)*(x**3+1))

In [159]: z
Out[159]: 
      -2⋅k    
      ─────   
        3     
  (-1)        
──────────────
3 ___ ⎛ 3    ⎞
╲╱ y ⋅⎝x  + 1⎠

双重积分变为：

In [164]: iiz =z.integrate((y, -x**3,0)).integrate((x,0,3))

In [165]: iiz
Out[165]: 
             -2⋅k          
             ─────         
     2/3       3           
-(-1)   ⋅(-1)     ⋅log(28) 
───────────────────────────
             2

执行 iiz.subs({k:0}) 等操作会生成上述复杂解决方案。

- hpaulj

网页内容由stack overflow 提供, 点击上面的

可以查看英文原文，
原文链接

- Wrzlprmft · Accepted Answer

你的问题是sympy.root默认返回主根而不是实数根。为了避免这种情况，你可以使用sympy.root的第三个可选参数来指定你需要实数根。以下代码将产生所需的结果：

import sympy as sp

x, y = sp.symbols('x y', real=True)
z = 1 / (sp.root(y,3,1)*(x**3+1))
iz = z.integrate((y, -x**3, 0))
iiz = iz.integrate((x, 0, 3))
print(iiz)
# -log(28)/2

为了回答你的问题，(-x**3)**(2/3) 实际上是 (-x**3)**0.666666666666667，因为这里出现了一个Python分数。如果想得到更接近你所需答案的结果，你需要进行以下操作：

import sympy as sp
x = sp.symbols('x', positive=True)
solution = (-x**3)**sp.Rational(2,3)
print(solution)
# (-1)**(2/3)*x**2

通常情况下，我建议避免使用有理数次方，除非你真的需要考虑到它们的多个解、复杂性等方面。

为什么SymPy不能将(-x**3)**(2/3)简化为x**2？

为什么SymPy不能将(-x3)(2/3)简化为x**2？