如何使堆的构建时间复杂度为O(n)？

Question

有人能帮忙解释如何将构建堆的时间复杂度优化到O(n)吗？

将一个项目插入到堆中的时间复杂度为O(log n)，并且插入操作会重复进行n/2次（余下的是叶子节点，不会违反堆属性）。因此，这意味着时间复杂度应该是O(n log n)。

换句话说，对于每个我们“堆化”的项目，它有可能需要向下过滤（即下滤）每个已经存在的堆层级一次（这个堆的层数为log n）。

我漏掉了什么？

- GBa

---

你说的“building”堆是什么意思？ - mfsiega

就像在堆排序中一样，取一个未排序的数组，并过滤掉顶部一半的元素，直到符合堆的规则。 - GBa

我能找到的唯一东西就是这个链接： Buildheap 的复杂度似乎为 Θ(n lg n) - n 次调用 Heapify，每次调用的成本为 Θ(lg n)，但这个结果可以改进为 Θ(n)。http://www.cs.txstate.edu/~ch04/webtest/teaching/courses/5329/lectures/heap-comp.pdf - GBa

请看这个麻省理工学院的视频：讲得很清楚，解释了如何用一点点数学推导出O(n)。 https://www.youtube.com/watch?v=B7hVxCmfPtM - CodeShadow

@CodeShadow提到的解释的直接链接：https://youtu.be/B7hVxCmfPtM?t=41m21s - sha1

堆包含二叉树，将元素插入二叉树中需要logn的时间，对于n个元素的总时间是n*logn。 - Devanshu

Answer 1

我认为这个主题中隐藏了几个问题：

• 如何实现 buildHeap 以使其在 O(n) 时间内运行？
• 当正确实现时，如何证明 buildHeap 的运行时间为 O(n)？
• 为什么相同的逻辑不能使堆排序的运行时间从 O(n log n) 变为 O(n)？

如何实现 buildHeap 以使其在 O(n) 时间内运行？

通常，对于这些问题的回答集中于 siftUp 和 siftDown 之间的区别。正确选择 siftUp 和 siftDown 对于实现 buildHeap 并获得 O(n) 性能至关重要，但这并不能帮助人们理解 buildHeap 和堆排序的一般区别。实际上，正确实现 buildHeap 和 heapSort 都只使用 siftDown。而 siftUp 操作仅在向现有堆中插入元素时才需要，因此它将用于实现使用二叉堆的优先级队列，例如。

我编写了这篇文章来描述最大堆的工作方式。这是通常用于堆排序或优先级队列（其中较高的值表示较高的优先级）的堆类型。最小堆也很有用；例如，在以升序排列具有整数键或按字母顺序排列具有字符串键的项时。原则完全相同，只需改变排序顺序即可。

堆属性 指定二叉堆中每个节点必须至少与其两个子节点一样大。特别是，这意味着堆中最大的项在根处。下移和上移本质上是相反方向的同一操作：将有问题的节点移动到满足堆属性的位置：

• siftDown 将一个太小的节点与其最大的子节点交换（从而将其向下移动），直到它至少与其下面的两个节点一样大。
• siftUp 将一个太大的节点与其父节点交换（从而将其向上移动），直到它不比其上面的节点更大。

siftDown和siftUp所需操作的次数与节点需要移动的距离成正比。对于siftDown，它要移动到树底的距离，因此对于在树顶的节点而言，siftDown是昂贵的。而对于siftUp，其工作量与到达树顶的距离成正比，因此对于在树底的节点而言，siftUp是昂贵的。尽管两种操作在最坏情况下都是O(log n)，但在堆中，只有一个节点在顶部，而一半的节点位于底层。因此如果我们必须对每个节点应用操作，那么我们更喜欢使用siftDown而不是siftUp。 buildHeap函数接受一个未排序项目的数组，并将它们移动，直到它们全部满足堆属性，从而生成一个有效的堆。使用我们描述的siftUp和siftDown操作，可以采用两种方法之一来实现buildHeap。

1. 从堆的顶部（数组的开头）开始，在每个项目上调用siftUp 。在每一步中，先前筛选的项目（当前项目在数组中的前一个项目）形成一个有效的堆，筛选下一个项目将其放置到堆的有效位置。在筛选每个节点之后，所有项目都满足堆属性。 2. 或者，相反地，从数组的末尾开始向前移动。在每次迭代中，将一个项目筛选到正确的位置。

哪种实现方式更高效呢？这两种方法都会产生一个有效的堆。不出所料，使用siftDown的第二种操作更高效。

假设h = log n表示堆的高度，则采用siftDown方法所需的工作量由以下总和给出：

(0 * n/2) + (1 * n/4) + (2 * n/8) + ... + (h * 1).

每个术语的总和都是给定高度节点将不得不移动的最大距离（对于底层为零，对于根为h）乘以该高度的节点数。相比之下，对于调用siftUp中的每个节点的总和为

(h * n/2) + ((h-1) * n/4) + ((h-2)*n/8) + ... + (0 * 1).

很明显第二个求和式更大。第一项单独为hn/2 = 1/2 n log n，因此这种方法的复杂度最好为O(n log n)。

我们如何证明siftDown方法的求和确实是O(n)？

一种方法（还有其他分析方法也可行）是将有限求和转化为无限级数，然后使用泰勒级数。 我们可以忽略第一项，即零：

如果您不确定每个步骤为什么有效，请看下面的文字解释：

• 各项都是正数，因此有限求和必须小于无限求和。
• 该级数等于在x=1/2处评估的幂级数。
• 该幂级数等于Taylor级数的导数，其中f(x)=1/(1-x)。
• x=1/2在该Taylor级数的收敛区间内。
• 因此，我们可以用1/(1-x)替换Taylor级数，求导并评估来找到无限级数的值。

由于无限和正好为n，因此我们得出有限和不大于O(n)。

为什么堆排序需要O(n log n)的时间？

如果可以在线性时间内运行buildHeap，那么为什么堆排序需要O(n log n)的时间呢？ 好吧，堆排序分为两个阶段。 首先，我们在数组上调用buildHeap，如果实现最佳，则需要O(n)的时间。 接下来的阶段是重复删除堆中最大的项并将其放在数组的末尾。 因为我们从堆中删除一个项目，所以总是有一个开放的位置位于堆的末尾之后，我们可以在那里存储该项目。 因此，堆排序通过连续删除下一个最大的项目并将其放入数组中，从最后一个位置开始并向前移动，实现排序顺序。 在堆排序中，这最后部分的复杂度是支配性的。循环如下：

for (i = n - 1; i > 0; i--) {
    arr[i] = deleteMax();
}

很明显，循环运行O(n)次（n-1确切地说，因为最后一项已经就位）。堆的deleteMax复杂度为O(log n)。通常情况下，它通过删除堆中剩余的最大项即根节点，并用堆中的最后一项即叶子节点替换它来实现。这个新的根节点几乎肯定违反了堆性质，所以你必须调用siftDown直到把它移回到一个可接受的位置。这也会将下一个最大的项移到根节点。请注意，与buildHeap不同的是，对于大多数节点，我们在从树底部调用siftDown，而现在我们在每个迭代中从树顶部调用siftDown！虽然树正在缩小，但缩小得不够快：树的高度保持不变，直到删除了前半部分的节点（当您彻底清除了底层时）。然后对于下一个四分之一，高度为h-1。因此，第二阶段的总工作量为

h*n/2 + (h-1)*n/4 + ... + 0 * 1.

注意到这个开关：现在零工作情况对应一个单一节点，而 h 工作情况对应一半的节点数。这个总和是 O（n log n），就像使用siftUp实现的低效版本的 buildHeap 一样。但在这种情况下，我们别无选择，因为我们试图进行排序并且我们需要下一个最大的项被下一个删除。

综上所述，堆排序的工作是两个阶段的总和：O（n）的buildHeap时间和 O（n log n）以按顺序删除每个节点，因此复杂度为O（n log n） 。您可以证明（使用一些信息论思想），对于基于比较的排序，希望 O（n log n）是您能够实现的最佳结果，因此没有理由对此感到失望或期望堆排序实现 buildHeap 的O（n）时间限制。

- Jeremy West

---

我编辑了我的回答，使用最大堆，因为似乎大多数人都在提到它，并且对于堆排序来说这是最好的选择。 - Jeremy West

这就是让我直观地明白的原因：“只有一个节点在顶部，而一半的节点位于底层。因此，如果我们必须对每个节点应用操作，我们会更喜欢使用siftDown而不是siftUp，这并不令人感到太惊讶。” - Vicky Chijwani

“一种方法是从堆的顶部（数组的开头）开始，并对每个项目调用siftUp。”- 你是否意味着从堆的底部开始？ - aste123

没错，原文写得正确。其想法是在数组满足堆属性的部分和未排序部分之间保持一个障碍。你可以从开头开始向前移动并对每个项调用siftUp，或者从末尾开始向后移动并调用siftDown。无论选择哪种方法，都是选择未排序部分中的下一项，并执行相应的操作，将其移动到有序部分中的有效位置。唯一的区别在于性能。 - Jeremy West

如果这个回答包括一个 O(n) 堆构建的伪代码实现，它对大多数读者的效用会得到极大提升。 - temporary_user_name

Answer 2

你的分析是正确的，但不够严密。

关于为什么建立堆是线性操作，这并不容易解释清楚，最好还是自己去阅读一下。

可以在这里看到该算法的一份非常好的分析。

---

主要思想是，在build_heap算法中，实际的heapify成本并不是对于所有元素都是O(log n)。

当调用heapify时，运行时间取决于元素在过程结束之前可能向下移动多远。换句话说，它取决于元素在堆中的高度。在最坏情况下，元素可能会一直下降到叶子层。

让我们逐层计算完成的工作量。

在最底层，有2^(h)个节点，但我们不会在任何一个节点上调用heapify，因此工作量为0。在下一层有2^(h−1)个节点，每个节点最多可能下降1层。在从底部算起的第3层，有2^(h−2)个节点，每个节点最多可能下降2级。

正如你所看到的，并不是所有的heapify操作都是O(log n)的，这就是为什么你得到O(n)的原因。

- emre nevayeshirazi

---

这是一个很好的解释...但是为什么堆排序的时间复杂度是 O(n log n) 呢？为什么相同的推理不能适用于堆排序呢？ - hba

我认为你问题的答案在于理解来自 这篇文章 的此图。当使用 siftDown 时，Heapify 是 O(n)，但当使用 siftUp 时，Heapify 是 O(n log n)。由于实际排序（逐个从堆中取出项目）必须使用siftUp，因此其时间复杂度是 O(n log n)。 - The111

我很喜欢你外部文件底部的直观解释。 - Lukas Greblikas

@hba，Jeremy West在下面的回答中更详细、易于理解地回答了你的问题，进一步解释了The111在这里的评论答案。 - cellepo

@hba 建立堆对于一半的值需要0个操作，对于四分之一的值需要1个操作，对于1/8的值需要2个操作等等，总时间复杂度为O(N)。在进行堆排序时，_所有_操作都需要log n的时间，因为您总是从顶部删除一个项目，然后将新项目插入到最昂贵的位置 - 顶部。 - gnasher729

Answer 3

直观上:

"复杂度应该是O(nLog n)... 对于每个要进行堆化的元素，它有可能需要过滤掉到目前为止堆的每一层一次（这是log n层）。”

不完全正确。您的逻辑没有产生紧密的边界 - 它高估了每个堆化(heapify)的复杂度。如果从底部构建，则插入(堆化)可以远少于O(log(n))。 过程如下：

( 第1步 ) 前n/2个元素放在堆的底部行。h = 0，因此不需要堆化。

( 第2步 ) 接下来的n/22个元素放在离底部1行的位置。h = 1，堆化向下过滤1层。

( 第i步 ) 接下来的n/2i个元素放在距离底部i行的位置。h=i，堆化向下过滤i层。

( 第log(n)步 ) 最后一个n/2log2(n) = 1个元素放在距离底部log(n)行的位置。h=log(n)，堆化向下过滤log(n)层。

注意: 在第一步之后，有1/2的元素(n/2)已经在堆中了，我们甚至不需要调用一次堆化(heapify)。 另外，请注意只有一个元素(根节点)需要承受完整的log(n)复杂度。

---

理论上:

建立一个大小为n的堆需要进行总共N步操作，这个数学公式可以表示出来。

在高度为i的位置，我们已经证明(上面)，需要执行叫做heapify的函数的元素数量为n/2^(i+1)，而且我们知道在高度为i的位置执行heapify函数的复杂度是O(i)。如下：

综合以上内容，得到以下公式：

对于最后一个求和式的解，我们可以通过对广为人知的等比级数方程两边取导数来找到。

最后，将x = 1/2代入上述方程式会得到2。将此值代入第一个公式得到：

因此，总步骤数是O(n)级别的。

- bcorso

---

非常感谢。为什么您决定插入x=1/2呢？ - Avv

由于ix^i的无限求和公式为x/(1-x)^2，因此当x=1/2时，i(1/2)^i与i*x^i相同。 - juancamilo87

Answer 4

已经有一些很好的答案了，但我想添加一个简单的可视化解释。

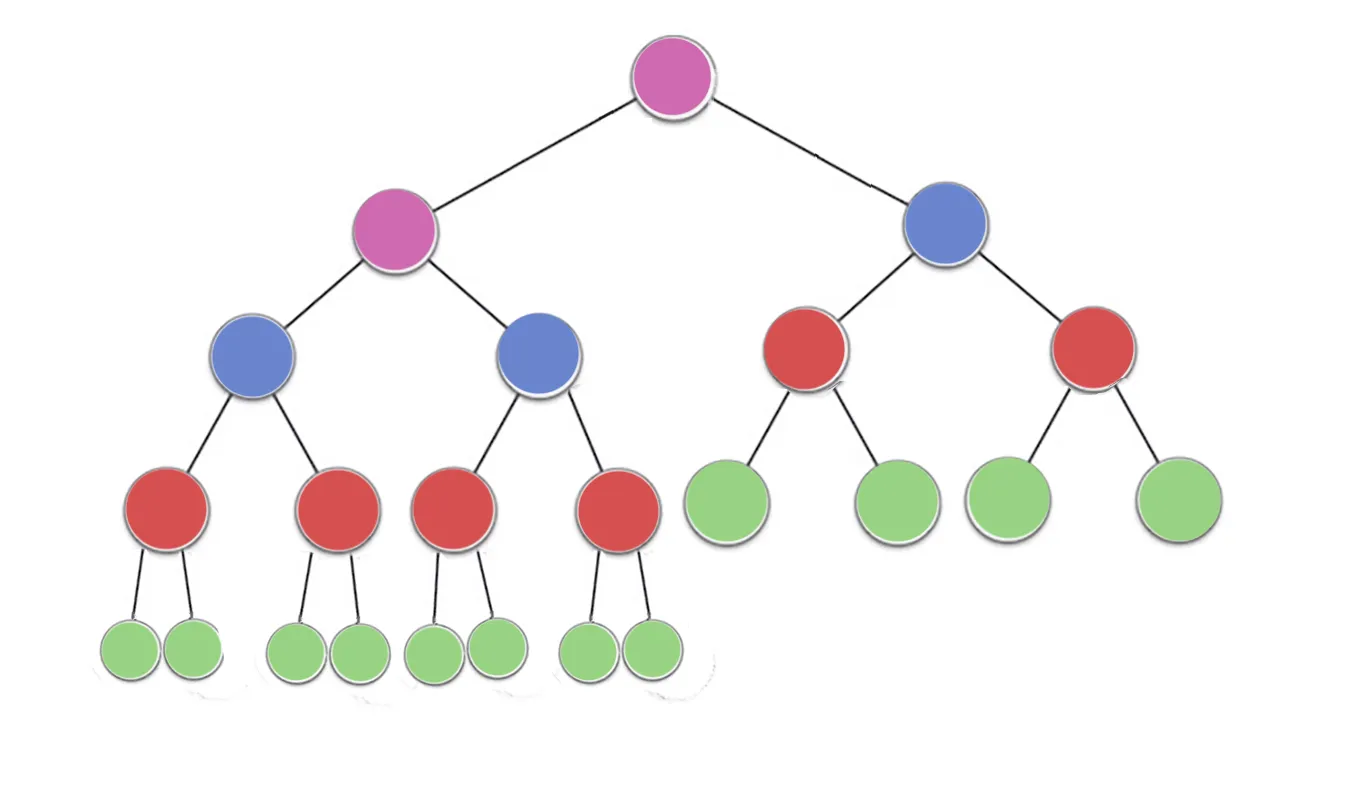
现在看看这张图片，它有以下几个部分：
n/2^1 绿色节点，高度为0（这里是23/2 = 12）
n/2^2 红色节点，高度为1（这里是23/4 = 6）
n/2^3 蓝色节点，高度为2（这里是23/8 = 3）
n/2^4 紫色节点，高度为3（这里是23/16 = 2）
所以对于高度h，有n/2^(h+1)个节点。
为了找到时间复杂度，让我们计算每个节点执行的工作量或迭代次数最大值
现在可以注意到每个节点最多可以执行迭代次数等于节点高度

Green  = n/2^1 * 0 (no iterations since no children)  
red    = n/2^2 * 1 (heapify will perform atmost one swap for each red node)  
blue   = n/2^3 * 2 (heapify will perform atmost two swaps for each blue node)  
purple = n/2^4 * 3 (heapify will perform atmost three swaps for each purple node)   

对于任何高度为h的节点，最大工作量为n/2^(h+1) * h

现在总工作量为

->(n/2^1 * 0) + (n/2^2 * 1)+ (n/2^3 * 2) + (n/2^4 * 3) +...+ (n/2^(h+1) * h)  
-> n * ( 0 + 1/4 + 2/8 + 3/16 +...+ h/2^(h+1) ) 

现在对于任何一个 h 的值，这个序列

-> ( 0 + 1/4 + 2/8 + 3/16 +...+ h/2^(h+1) ) 

永远不会超过1
因此，构建堆的时间复杂度将永远不会超过O(n)

因此，构建堆的时间复杂度将永远不会超过O(n)

- Julkar9

---

这是有史以来最好的解释。 - IamMashed

Answer 5

如果您通过重复插入元素来构建堆，则时间复杂度为O(n log n)。但是，您可以通过以任意顺序插入元素，然后应用算法将它们“堆化”为正确的顺序（根据堆的类型）来更有效地创建新堆。

请参见http://en.wikipedia.org/wiki/Binary_heap，“Building a heap”中的示例。在这种情况下，您基本上从树的底层开始工作，交换父节点和子节点，直到满足堆条件为止。

- mike__t

Answer 6

众所周知，堆的高度为log(n)，其中n是元素的总数。我们将其表示为h。当我们执行堆化操作时，最后一层（h）的元素不会移动。倒数第二层（h-1）的元素数量为2^（h-1），它们最多可以在堆化期间移动1个级别。同样，对于第i层，我们有2^i个元素，可以移动h-i个位置。 因此，移动的总次数为： S = 2^h*0 + 2^(h-1)*1 + 2^(h-2)*2 + ...2^0*h S=2^h {1/2 + 2/2^2 + 3/2^3 + ... h/2^h} ---------------------------------1 这是一个AGP序列，为了解决它，将两边除以2： S/2 = 2^h {1/2^2 + 2/2^3 + ... h/2^(h+1)} -------------------------------2

从等式1中减去等式2得到：
S/2=2^h {1/2+1/2² + 1/2³+ ...+1/2^h+ h/2^h+1}
S=2^h+1 {1/2+1/2² + 1/2³+ ...+1/2^h+ h/2^h+1}

现在，1/2+1/2² + 1/2³+ ...+1/2^h是递减的等比数列，其和小于1（当h趋近于无穷大时，总和趋近于1）。在进一步分析中，让我们取一个上界，即1。

这给出：
S=2^h+1{1+h/2^h+1}
  =2^h+1+h
  ~2^h+h

由于h=log(n)，2^h=n

因此，S=n+log(n)
T(C)=O(n)

- Tanuj Yadav

Answer 7

在构建堆时，假设你采用自下而上的方法。

1. 你会对每个元素进行比较，检查它是否符合堆规则和其子节点是否合适。因此，叶子节点不需要额外处理，因为它们没有子节点。 2. 向上移动，在叶子节点上面的最坏情况是只需要进行一次比较（他们最多只需要与一代孩子进行比较）。 3. 进一步向上移动，他们的直接父节点最多可以与两代孩子进行比较。 4. 继续沿着同样的方向，最坏情况下根节点需要 log(n) 次比较，其直接子节点需要 log(n)-1 次比较，其直接子节点需要 log(n)-2 次比较，以此类推。 5. 把上述内容加总起来，你得到的是类似于 log(n) + {log(n)-1}*2 + {log(n)-2}*4 + ..... + 1*2^{(logn)-1} 的表达式，这就是 O(n)。

- Jones

Answer 8

我们通过确定每个节点可以移动的最大距离来获取堆构建的运行时。因此，我们需要知道每一行有多少个节点以及每个节点可以到达的距离。

从根节点开始，下一行的节点数是前一行的两倍，因此，通过回答我们可以将节点数量加倍多少次，直到没有任何节点剩余为止，我们得到树的高度。或者用数学术语来说，树的高度是log2（n），其中n是数组的长度。

为了计算一行中的节点数，我们从后面开始，我们知道n/2个节点在底部，因此通过除以2，我们得到上一行，以此类推。

基于此，我们得到Siftdown方法的公式： (0 * n/2) + (1 * n/4) + (2 * n/8) + ... + (log2(n) * 1)

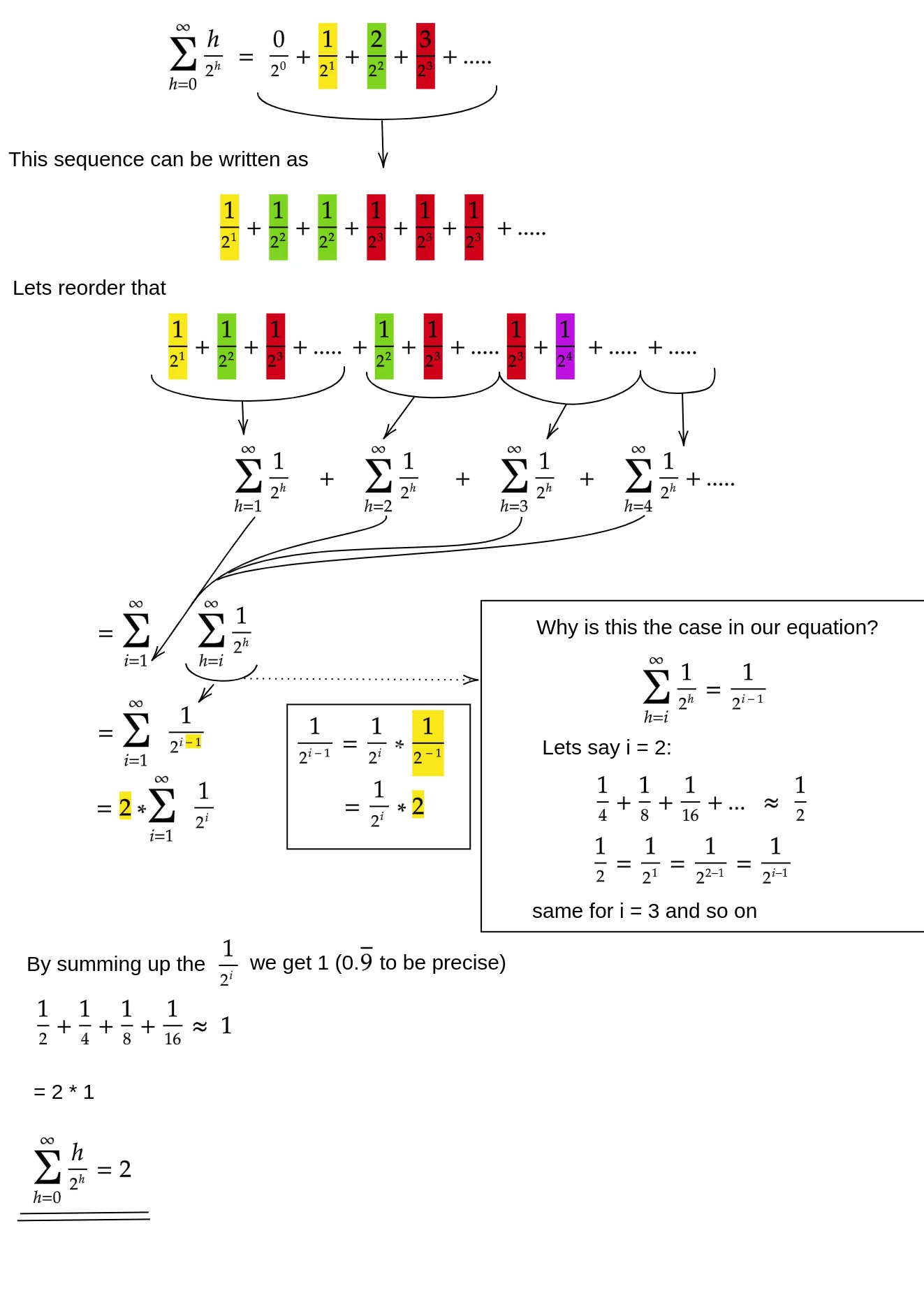最后一个括号中的项是树的高度乘以在根处的一个节点，第一个括号中的项是底部行中的所有节点乘以它们可以移动的距离，即0. 同样的智能公式如下： 将n带回来，我们得到2 * n，2可以丢弃，因为它是一个常数，我们就得到了Siftdown方法的最差运行时：n。

- Max Tromp

Answer 9

简短回答

使用 Heapify() 构建二叉堆需要 O(n) 时间。

当我们逐步添加元素到堆中并在每一步保持堆属性（最大堆或最小堆）时，总时间复杂度将为 O(nlogn)。因为二叉堆的一般结构是完全二叉树，所以堆的高度为 h = O(logn)。因此，将一个元素插入堆中所需的时间等同于树的高度，即 O(h) = O(logn)。对于 n 个元素，这将花费 O(nlogn) 的时间。

现在考虑另一种方法。为了简单起见，我假设我们有一个最小堆。因此，每个节点都应该比它的子节点小。

1. 将所有元素添加到完全二叉树的框架中。这将花费 O(n) 的时间。
2. 现在我们只需要以某种方式满足最小堆属性。
3. 由于所有叶子节点没有子节点，它们已经符合堆的属性。叶子节点的总数为 ceil(n/2)，其中 n 是树中存在的元素的总数。
4. 对于每个内部节点，如果它大于其子节点，则以从下到上的方式将其与最小的子节点交换位置。对于每个内部节点，这将花费 O(1) 的时间。注意:我们不会像插入时那样将值向上交换到根。我们只交换一次，以便以该节点为根的子树是一个适当的最小堆。
5. 在基于数组的二叉堆实现中，我们有 parent(i) = ceil((i-1)/2)，i 的子节点由 2*i + 1 和 2*i + 2 给出。因此，通过观察，我们可以说数组中的最后 ceil(n/2) 个元素是叶节点。深度越深，节点的索引就越大。我们将对 array[n/2]，array[n/2 - 1]......array[0] 重复 步骤4。通过这种方式，我们确保以从底部到顶部的方式执行此操作。总体而言，我们最终将维护最小堆属性。
6. 对于所有 n/2 元素的 步骤4 将花费 O(n) 的时间。

因此，使用这种方法进行堆化的总时间复杂度为 O(n) + O(n) ~ O(n)。

- Pratyush Ranjan

Answer 10

我们可以使用另一种最优解来构建堆，而不是重复插入每个元素。具体步骤如下：

• 将n个元素任意放入数组中，以遵守堆的形状属性。
• 从最低层开始向上移动，像堆化-向下过程一样将每个子树的根节点向下筛选，直到恢复堆属性。

这个过程可以用以下图片说明：

接下来，让我们分析一下上述过程的时间复杂度。假设堆中有n个元素，堆的高度为h（对于上面图片中的堆来说，高度为3）。那么我们应该有以下关系：

当最后一层只有一个节点时，n = 2^h。当树的最后一层完全填满时，n = 2^(h+1)。

从底部开始作为第0级（根节点是第h级），在第j级中，最多有2^(h-j)个节点。每个节点最多需要进行j次交换操作。因此，在第j级中，操作的总数为j*2^(h-j)。

因此，构建堆的总运行时间与以下成比例：

如果我们将2^h项分解出来，那么我们得到：

正如我们所知，∑j/2ʲ是一个收敛于2的级数（详细内容可以参考this wiki）。

利用这个结果，我们有：

基于条件2^h <= n，因此我们有：

现在我们证明建立堆是一种线性操作。

- Chris Bao