子三角形最大元素之和

Question

子三角形最大元素之和

6

我尝试解决了今年CCC 2019 S5的最后一个问题。

问题陈述:

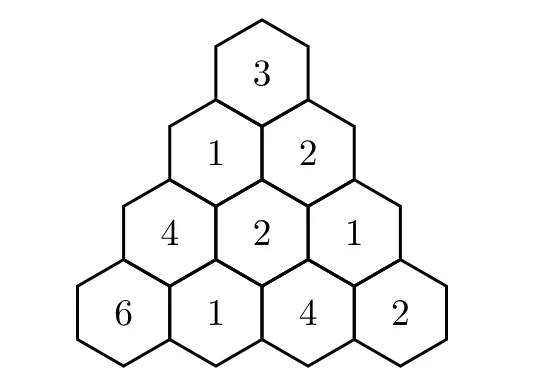
在一个平行宇宙中，计算机科学中最重要的数据结构是三角形。大小为M的三角形包含M行，第i行包含i个元素。此外，这些行必须排列成等边三角形的形状。也就是说，每一行都以垂直通过三角形中心的对称线为中心。例如，下图显示了一个大小为4的三角形：

三角形包含子三角形。例如，上面的三角形包含1个大小为1的子三角形、6个大小为2的子三角形（其中包括包含(3,1,2)和包含(4,6,1)的三角形），3个大小为3的子三角形（其中包括包含(2,2,1,1,4,2)的三角形）。请注意，每个三角形都是其自身的子三角形。

给定大小为N的三角形，必须找到所有大小为K的子三角形的最大元素的总和。

输入格式

第一行包含两个以空格分隔的整数N和K（1≤K≤N≤3000）。

接下来N行描述三角形。其中第i行包含i个以空格分隔的整数ai，j（0≤ai，j≤10^9），表示三角形的第i行。

对于15个可用分数中的4个，N≤1000。

输出格式

输出大小为K的所有子三角形的最大元素的总和。

样本输入

样例输入的输出结果

很不幸，我的解决方案被判定为TLE，并且我不知道如何对其进行优化。

这个问题基本上是要求找到子三角形的最大元素并将它们相加。我的方法很直接，我迭代了大三角形的每个元素，使它们成为子三角形的“根”，然后尝试去每个元素中寻找最大值并将它们加到结果中。

我需要一些帮助来改进我的解决方案，是否需要某种数据结构？

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

int main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    vector<vector<int>> triangle;

    int n;
    int k;

    cin >> n >> k;

    for (int i = 0; i < n; ++i)
    {
        triangle.push_back(vector<int>(i + 1, 0));

        for (int j = 0; j <= i; ++j)
            cin >> triangle[i][j];
    }

    int sum = 0;

    for (int level = 0; level <= n - k; ++level)
        for (int root = 0, size1 = triangle[level].size(); root < size1; ++root)
        {
            int largest = 0;

            for (int i = level, counter = 0; i < level + k; ++i, ++counter)
                for (int j = root, times = 0, size2 = triangle[i].size(); j < size2 && times <= counter; ++j, ++times)
                    largest = max(largest, triangle[i][j]);

            sum += largest;
        }

    cout << sum << "\n";

    return 0;
}

- Jimmy Y.

2个回答

1

这是我的解决方案：

#include <iostream>
#include <vector>

using namespace std;

int max3(int a, int b, int c)
{
    return max(a, max(b,c));
}

int main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    int n,k;
    cin>>n>>k;
    vector<vector<long long>> triangle;
    for(int i = 0; i < n; i++)
    {
        triangle.push_back(vector<long long>(i + 1, 0));
        for (int j = 0; j <= i; j++)
            cin >> triangle[i][j];
    }
    for(int size = 2; size <= k; size++)
        for(int i = 0;i <= n - size; i++)
            for(int j = 0; j <= i; j++)
                triangle[i][j] = max3(triangle[i][j], triangle[i+1][j+1], triangle[i+1][j]);
    long long sum = 0;
    for(int i = 0;i <= n - k; i++)
        for(int j = 0; j <= i; j++)
            sum += triangle[i][j];
    cout<<sum;
}

解释：我们将三角形的最上面的正方形称为三角形的顶部。假设t(i, j, k)是以i, j为顶部，大小为k的三角形中最大的数字。从这里我们可以得出以下事实：

t(i, j, 1) = triangle[i][j]
每个以(i, j)为顶部，大小为k>=2的三角形都可以由大小为k-1，顶部分别为(i, j)、(i+1, j)和(i+1, j+1)的三个三角形的并集组成。
因此，以(i, j)为顶部，大小为k>=2的三角形中最大的数字将是这三个三角形中最大数字的最大值，或者用公式表示为：
t(i, j, k) = max( t(i, j, k-1), t(i+1, j, k-1), t(i, j+1, k-1) )

所以我们需要做的就是存储前一个k的三角形的最大值。由于我们将从三角形的顶部开始迭代，因此可以覆盖其中的当前值，因为该公式仅使用其下方和本身的三角形来计算新k的值。程序应从size = 2开始，并通过使用旧值计算所有大小的新值，直到k。我还使用long long，因为安全第一。希望这有所帮助！

- Nick Nikolov

2

这不是Theta(n^2 k)时间吗？如果是，那似乎太慢了。 - David Eisenstat

对于 1≤K≤N≤3000 的值，它几乎是瞬间完成的。 - Nick Nikolov

请您能否在您的代码中添加一个随机数的例子？ - גלעד ברקן

网页内容由stack overflow 提供, 点击上面的

可以查看英文原文，
原文链接

- btilly · Accepted Answer

这里有一个可以实现O(n^2 log(k))的解决方案，速度足够快。

思路是这样的：从大小为1的三角形的nxn三角形到大小为2的三角形的最大值的(n-1)x(n-1)三角形的过程是一个 O(n) 的操作。只需将每个三角形与其相邻三角形的最大值进行比较即可。

同样的技巧可以用来从第二个三角形转到大小为2的三角形的最大值的(n-1)x(n-1)三角形。但是，如果你在每个方向上跳过一个，则可以直接到达大小为4的三角形的最大值的(n-3)x(n-3)三角形中。也可以在O(n)时间内完成。举例说明后一种情况，假设我们的起点是：

为了得到大小为2的三角形，我们将每个三角形与其相邻的三角形进行比较。

为了得到大小为4的三角形，比较时跳过一个，因此我们比较底部的6、3、4。接下来我们比较4、4、5等等。

 5
6 5

然后我们将它们加在一起得到11。

接下来，从大小为4的三角形中最大值的(n-3)x(n-3)三角形，你可以通过选择要比较的三角形的大小来直接进入大小为5、6、7或8的三角形的最大值的三角形，跳过1个、2个或3个。

如此反复进行，以得到k乘k三角形中最大值的三角形，其中包含O(log(k))步。