凸包中的最大三角形

Question

这个问题已经得到了答复，但我面临的主要问题是理解其中一个答案。

From https://dev59.com/13I-5IYBdhLWcg3w487k#1621913

以下算法如何达到O(n)？

首先，通过对点进行排序/计算凸包（在O(n log n)时间内），如果必要的话，我们可以假设我们有带有点的凸多边形/壳，这些点按照它们在多边形中出现的顺序循环排序。将点1、2、3、...、n称为A、B和C（变量），分别从1、2和3开始（按循环顺序）。我们将移动A、B、C直到ABC是最大面积三角形。（这个想法类似于旋转卡尺方法，在计算直径（最远对）时使用。）

固定A和B，向前推进C（例如，最初，当A=1，B=2时，C通过C=3、C=4等向前推进），只要三角形的面积增加，即只要Area(A,B,C) ≤ Area(A,B,C+1)，就继续前进。这个点C将最大化那些固定的A和B的Area(ABC)。（换句话说，函数Area(ABC)作为C的函数是单峰的。）

接下来，如果这样可以增加面积，就提高B的值（不改变A和C）。如果是这样，请像上面那样再次提高C的值。然后再次提高B的值（如果可能的话），等等。这将给出以A为一个顶点的最大面积三角形。（前面的部分应该很容易证明，分别对每个A单独执行此操作将会得到O(n2)。但请继续阅读。）现在，如果提高A的值可以改善面积，则继续执行。

- aiccha

Answer 1

作为问题主题的答案的作者，我觉得有必要对O(n)运行时间进行更详细的解释。

---

首先，这里有一张来自论文的图示，展示了算法的前几个步骤，以一个特定的样本输入（一个12边形）为例。首先我们从A、B、C三个相邻的顶点开始（图中的第1步），C向前推进直到面积增加（第2到6步），然后推进B，以此类推。

上面带星号的三角形是“锚定的局部最大值”，即对于给定的A最好的三角形（即推进C或B都会减少面积）。

---

关于运行时间为O(n)：让B的“实际”值，以它被递增的次数为基础并忽略回绕，为nB，同样地，对于C也是如此，为nC。（换句话说，B = nB % n和C = nC % n。）现在注意，

1. （“B在A前面”）无论A的值如何，我们都有A ≤ nB < A + n

2. nB总是在增加

因此，当A从0到n变化时，我们知道nB只在0到2n之间变化：它最多可以递增2n次。同样的道理也适用于nC。这表明算法的运行时间（与A、B和C被递增的总次数成比例）受到O(n) + O(2n) + O(2n)的限制，即O(n)。

- ShreevatsaR

Answer 2

这样考虑：每个A,B,C都是指针，它们在任何时候都指向凸包中的一个元素。由于算法增加它们的方式，每个指针最多只会指向凸包中的每个元素一次。因此，每个指针都会迭代一个由O(n)元素组成的集合。它们不会被重置，一旦其中一个指针通过了一个元素，它将永远不再通过该元素。

由于有3个指针(A,B,C)，所以时间复杂度为 3 * O(n) = O(n)。

编辑:

由于代码是在提供的链接中呈现的，因此可能不是O(n)，因为B和C围绕数组。然而，根据描述，这种包装似乎并不必要：在看到代码之前，我想象该方法将阻止B和C超过n。在这种情况下，它肯定是O(n)。然而，由于代码是按照这种方式呈现的，我不确定。

可能由于某些数学原因，B和C在整个算法中仍然只迭代O(n)次，但我无法证明这一点。 我也无法证明不包装（只要注意索引越界错误）是正确的。

- IVlad

---

这仅适用于一个A值，不是吗？我认为B和C可以再次迭代另一个A值？ - aiccha

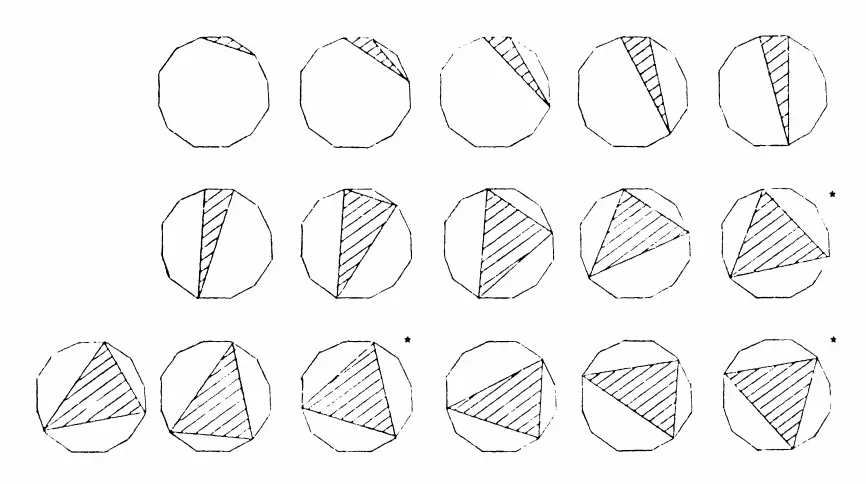
@aicha - 根据代码的呈现方式，这似乎是可能的，因为 B 和 C 围绕数组。然而，根据描述，这种环绕并不是必要的：在看到代码之前，我想象方法会停止 B 和 C 超过 n 的进展。在这种情况下，它肯定是 O(n)。由于代码的呈现方式，我不确定。出于某些数学原因，B 和 C 在整个算法中仍然只迭代 O(n) 次，但我无法证明。我也无法证明不进行环绕是正确的。 - IVlad