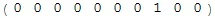R = {1,2，...，N}的子集列表S1，...，Sn，以及一个整数k。是否有一种有效的方法可以找到大小为k的R子集C，使得C是Si的最大数量的子集？R = {1,2,3,4}且k = 2。S1={1,2,3}
S2={1,2,3}
S3={1,2,4}
S4={1,3,4}
C={1,2}或C={1,3}（无所谓哪个）。假设我理解了你的问题，我认为对于相当小的集合来说这是很简单的。
我将使用Mathematica代码进行说明，但概念是通用的。
我从集合{1..8}中生成长度为4的10个随机子集：
ss = Subsets[Range@8, {4}] ~RandomSample~ 10
{{1, 3, 4, 6}, {2, 6, 7, 8}, {3, 5, 6, 7}, {2, 4, 6, 7}, {1, 4, 5, 8}, {2, 4, 6, 8}, {1, 2, 3, 8}, {1, 6, 7, 8}, {1, 2, 4, 7}, {1, 2, 5, 7}}
我将它们转换为每个子集中每个数字存在的二进制数组：
a = Normal@SparseArray[Join @@ MapIndexed[Tuples[{##}] &, ss] -> 1];
Grid[a]
这是十个子集的十列，以及元素{1..8}的八行。
现在生成所有可能的目标子集（大小为3）：
keys = Subsets[Union @@ ss, {3}];
取一个“键”，从数组中提取这些行并执行 BitAnd 操作（如果所有列都等于 1，则返回 1），然后计算其中的 1 的数量。例如，对于键 {1, 6, 8}，我们有：
a[[{1, 6, 8}]]
进行 BitAnd 后：
对于每个键，执行以下操作：
counts = Tr[BitAnd @@ a[[#]]] & /@ keys;
然后找出该列表中最大元素的位置，提取相应的keys部分：
keys ~Extract~ Position[counts, Max@counts]
{{1, 2, 7}, {2, 4, 6}, {2, 4, 7}, {2, 6, 7}, {2, 6, 8}, {6, 7, 8}}
如果有足够的内存，这个过程可以快速处理更大的数据集。从{1..30}中随机选择长度为7的子集，共选择50000个：
ss = Subsets[Range@30, {7}] ~RandomSample~ 50000;
大约需要九秒钟计算长度为4的最大子集：
AbsoluteTiming[
a = Normal@SparseArray[Join @@ MapIndexed[Tuples[{##}] &, ss] -> 1];
keys = Subsets[Union @@ ss, {4}];
counts = Tr[BitAnd @@ a[[#]]] & /@ keys;
keys~Extract~Position[counts, Max@counts]
]
我应该补充说明的是，Mathematica 是一种高级语言，这些操作是在通用对象上进行的，因此如果真正在二进制级别上完成这些操作，那么速度应该更快，内存效率也更高。{8.8205045, {{2, 3, 4, 20}, {7, 10, 15, 18}, {7, 13, 16, 26}, {11, 21, 26, 28}}}
k的子集，因为例如我有一个实例，其中N=1000和k=100，这意味着我将不得不生成约10^140个子集。 - mitchus{1, ..., N}，如果集合包含该整数，则它们之间有一条边。然后，找到一个大小为 k 的公共子集，它是最大数量的 Si 的子集，等价于找到一个具有最大边数 i*k 的完全二分子图 K(i, k)。如果你能在多项式时间内完成这个任务，那么你可以通过尝试每个固定的 k 在多项式时间内找到具有最大边数 i*j 的完全二分子图 K(i, j)。但是，这个问题是NP完全问题（完全二分图），所以除非P=NP，否则你的问题没有多项式时间算法。i*j的完全二分子图，而是在左侧寻找具有最大节点数i的子图。 - mitchusj（在您的问题中等于 k），这是等价的。因此，如果您可以在多项式时间内为每个（固定的）j 完成它，那么您可以通过搜索每个固定的 j 并保留最佳结果来找到具有最大边数 i*j 的完全二分子图。 - Edouardj并为每个j值解决（子）问题。然后，解决NP-完全问题等同于解决N（子）问题（每个j值一个）。如果您可以在多项式时间内解决每个（子）问题，则解决N个问题的时间复杂度也是多项式的。 - Edouard希望我没有误解问题... 这里是SWI-Prolog的解决方案
:- module(subsets, [solve/0]).
:- [library(pairs),
library(aggregate)].
solve :-
problem(R, K, Subsets),
once(subset_of_maximal_number(R, K, Subsets, Subset)),
writeln(Subset).
problem(4, 2,
[[1,2,3], [1,2,3], [1,2,4], [1,3,4]]).
problem(8, 3,
[[1, 3, 4, 6], [2, 6, 7, 8], [3, 5, 6, 7], [2, 4, 6, 7], [1, 4, 5, 8],
[2, 4, 6, 8], [1, 2, 3, 8], [1, 6, 7, 8], [1, 2, 4, 7], [1, 2, 5, 7]]).
subset_of_maximal_number(R, K, Subsets, Subset) :-
flatten(Subsets, Numbers),
findall(Num-Count,
( between(1, R, Num),
aggregate_all(count, member(Num, Numbers), Count)
), NumToCount),
transpose_pairs(NumToCount, CountToNumSortedR),
reverse(CountToNumSortedR, CountToNumSorted),
length(Subset, K), % list of free vars
prefix(SolutionsK, CountToNumSorted),
pairs_values(SolutionsK, Subset).
测试输出：
?- solve.
[1,3]
true ;
[7,6,2]
true.
编辑：我认为上面的解决方案是错误的，因为返回的内容不能是任何输入的子集：这里是一个没有此问题的（注释掉的）解决方案：
:- module(subsets, [solve/0]).
:- [library(pairs),
library(aggregate),
library(ordsets)].
solve :-
problem(R, K, Subsets),
once(subset_of_maximal_number(R, K, Subsets, Subset)),
writeln(Subset).
problem(4, 2,
[[1,2,3], [1,2,3], [1,2,4], [1,3,4]]).
problem(8, 3,
[[1, 3, 4, 6], [2, 6, 7, 8], [3, 5, 6, 7], [2, 4, 6, 7], [1, 4, 5, 8],
[2, 4, 6, 8], [1, 2, 3, 8], [1, 6, 7, 8], [1, 2, 4, 7], [1, 2, 5, 7]]).
subset_of_maximal_number(R, K, Subsets, Subset) :-
flatten(Subsets, Numbers),
findall(Num-Count,
( between(1, R, Num),
aggregate_all(count, member(Num, Numbers), Count)
), NumToCount),
% actually sort by ascending # of occurrences
transpose_pairs(NumToCount, CountToNumSorted),
pairs_values(CountToNumSorted, PreferredRev),
% we need higher values first
reverse(PreferredRev, Preferred),
% empty slots to fill, preferred first
length(SubsetP, K),
select_k(Preferred, SubsetP),
% verify our selection it's an actual subset of any of subsets
sort(SubsetP, Subset),
once((member(S, Subsets), ord_subtract(Subset, S, []))).
select_k(_Subset, []).
select_k(Subset, [E|R]) :-
select(E, Subset, WithoutE),
select_k(WithoutE, R).
测试：
?- solve.
[1,3]
true ;
[2,6,7]
true.