找出覆盖所有点的最小面积的两个矩形。

Question

给定一个包含 n 个点的未排序数组，你需要找到两个矩形，覆盖所有点且它们不重叠。矩形的边应该平行于 x 或 y 坐标轴。
程序应返回所有这些点所覆盖的最小区域。第一个矩形的面积加上第二个矩形的面积。

我试图解决这个问题。我按 X 坐标对点进行排序，并将第一个点作为第一个矩形的最左侧点。当我们遍历点时，我们找到最高和最低的点。我认为当两个点之间的 x 差异最大时，第一个点是第一个矩形的最右侧点，第二个点是第二个矩形的最左侧点。
如果点的分布如第一个示例，则可以正常工作，但是如果是第二个示例，则无法正常运行。因为它会返回类似于这样的错误结果：

这应该是正确的：

然后我想进行两次排序，第二次按 Y 轴坐标排序，然后比较两个总面积。当点按 X 排序时的面积和当点按 Y 排序时的面积，取较小的面积作为正确答案。

- Strahinja

---

那么你对我们有什么期望？在这个问题中，“溢出”在哪里（你尝试过但卡在某个地方了）？ - haccks

我更新了问题。 - Strahinja

这是来自编程竞赛的问题吗？你能提供竞赛链接吗？ - fjardon

即使您更新了，问题仍然不清楚。您是否尝试了您想做的事情？结果是否如您所愿？ - AakashM

这是轴平行的两个矩形点集覆盖问题的变体，其中在“通过两个轴平行框覆盖一组点”[Bespamyatnikh，Segal 2000]中发表了一个O（nlogn）解决方案。在这个问题中，被最小化的函数（在其他选择中）是较大矩形的面积，而在您的问题中，应该被最小化的函数是矩形的面积之和。 - Lior Kogan

Answer 1

两个矩形不能重叠，因此一个必须完全在另一个右侧或上方。按x值对点进行排序并找到最大间隙的想法很好，但您应该针对两个方向执行此操作，就像您建议的那样。这将在您的示例中找到正确的矩形。

然而，最大间隙不一定是理想的分割点。根据垂直方向上的边界框范围，分割可能发生在其他地方。考虑一个带有四个象限的矩形区域，其中两个对角象限被点填充：

在这种情况下，理想的分割点不在最大间隙处。

           

考虑相邻 x 和 y 坐标点之间的所有可能分割，以找到理想位置。

• 按照 x 坐标对点进行排序。
• 升序扫描排序后的数组。通过存储最小和最大 y 坐标来跟踪当前点左侧的最小矩形。为每个点存储这些运行中的顶部和底部边界。
• 现在以降序方式执行相同操作，其中您保留右矩形的运行顶部和底部边界。
• 最后，再次循环遍历点，并计算相邻节点之间的分割的左右最小矩形的面积。跟踪最小面积总和。

然后对于最小顶部和底部矩形执行相同操作。最后两个步骤可以合并，这将为右矩形的最小边界保存数组。

这应该是 O(n·logn) 的时间复杂度：排序是 O(n·logn)，单个遍历的时间复杂度是 O(n)。您需要为第一个矩形的运行边界使用 O(n) 的额外内存。

- M Oehm

Answer 2

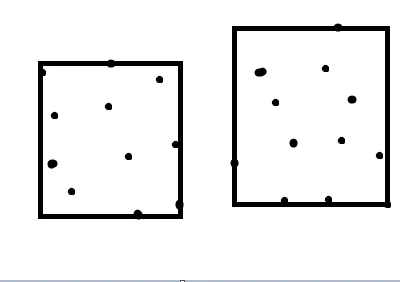
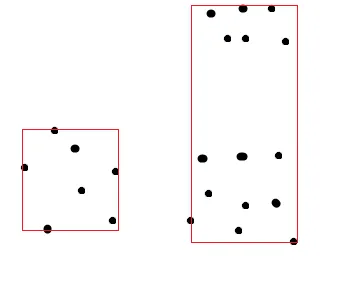
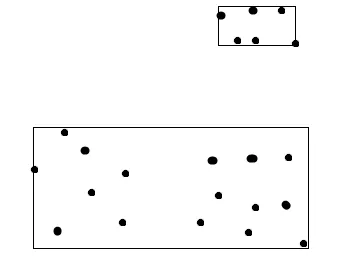
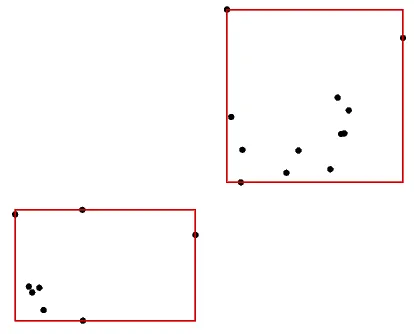
第一个观察结果是，矩形的任何一条边都必须接触其中一个点。没有接触点的边可以向后拉，从而减少面积。

给定n个点，因此共有n种选择左1、右1、底部1、顶部1、左2、右2、底部2和顶部2。这已经提供了一个简单的O(n^8)算法：尝试所有可能的分配，并记住给出最小总面积（right1-left1）（top1-bottom1）+（right2-left2）（top2-bottom2）的那个分配方案。确实，您可以跳过任何right<left或top<bottom的组合。这样可以加速，但不会改变O(n^8)的上限。

另一个观察结果是，边缘应保持在所有点的最小和最大X和Y边界内。找到任何点的最小和最大X和Y值。将它们称为minX、maxX、minY和maxY。你的矩形中至少有一个需要将其左、右、底部和顶部边缘分别置于这些水平线上。

因为minx、maxX、minY和maxY必须分配给两个矩形之一，并且有正好2^4=16种方法可以做到这一点，因此可以尝试使用如上所述的每个四个可能的分配中的每一个来分配剩余的坐标。这将得到一个O（n^4）算法：O(n)用于获取minX、maxX、minY和maxY，然后对于将minX、maxX、minY和maxY分配给8个边界坐标的16个分配中的每一个，需要O(n^4)时间来填充四个未分配变量。

到目前为止，我们忽略了矩形不重叠的要求。为了容纳这一点，我们必须确保以下至少一种情况成立：

1. 在Y坐标h上的水平线段，其中top1 <= h <= bottom2
2. 在Y坐标h上的水平线段，其中top2 <= h <= bottom1
3. 在X坐标w上的垂直线段，其中right1 <= h <= left2
4. 在X坐标w上的垂直线段，其中right2 <= h <= left1

如果同时满足以下四个条件，则两个矩形重叠，否则不重叠。这使我们能够跳过候选解，从而加快速度，但不改变渐近界限O(n^4)。请注意，我们需要特别检查此条件，否则最优解可能会有重叠（练习：展示这样的例子）。

让我们试着进一步缩短时间。根据上述第1个条件，假设我们有非重叠矩形。然后可以选择n个h值；我们可以尝试每个h值，然后通过找到结果两半中点的最小和最大坐标来确定所选区域的面积。通过尝试所有n个h值的选择，我们可以确定“最佳情况”垂直分割。我们无需尝试第2个条件，因为唯一的区别在于矩形的顺序是任意的。我们还必须使用水平分割尝试第3个条件。这建议了一个O(n^2)算法：

1. 对于每个点，选择h = point.y。
2. 将点分成两组，一组是point.y <= h，另一组是point.y > h。
3. 找到两个子集中X和Y坐标的最小值和最大值。
4. 计算两个矩形的面积之和。
5. 记住从上面得到的最小面积和相应的h。
6. 重复以上步骤，但使用w和X坐标。
7. 确定最小面积是通过垂直还是水平切割获得的。
8. 返回相应的矩形作为答案。

我们能做得更好吗？这是O(n^2)而不是O(n)，因为对于每个h和w的选择，我们需要扫描每个子组以找到最小和最大坐标。这假设通过两个子组进行线性扫描。事实上，当水平/垂直扫描时，我们不需要为min和max X/Y坐标执行此操作，因为那些将是已知的。我们需要解决的问题是：

给定n个点和一个值h，找到任何Y坐标不大于h的点的最大X坐标。

我提供的明显解决方案是O(n^2)，但你可能可以通过巧妙地应用排序找到一个O(n log n)的解决方案，甚至通过一些更聪明的方法找到一个O(n)的解决方案。我不会尝试这样做。

我们的解决方案是O(n^2)；理论上最优解是Omega(n)，因为您必须至少查看所有点。所以我们已经很接近了，但还有改进的空间。

- Patrick87