网格最小精确覆盖问题及额外切割

Question

这个问题出现在挑战中，但是由于现在已经关闭，所以可以问一下。

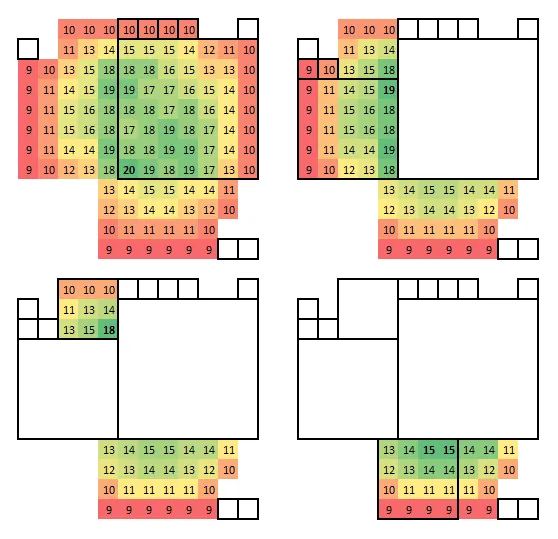
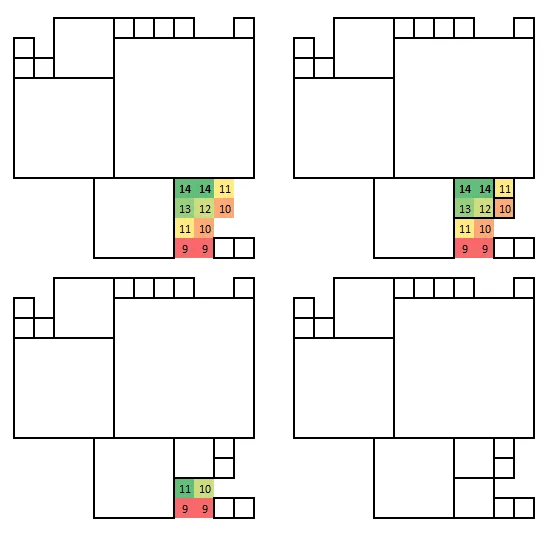
问题（不是这个问题本身，这只是背景信息）可以通过借用他们自己的图像来进行视觉描述：

我选择最优解决方案。对于决策变量来说，这可能是一个NP完全问题（它肯定属于NP，并且类似于精确覆盖问题，尽管我没有证明一般的精确覆盖问题可以归约到它），但这没关系，它只需要在实践中快速，不一定在最坏情况下快。在这个问题的背景下，除非它们提供切割，否则我对任何近似算法都不感兴趣。

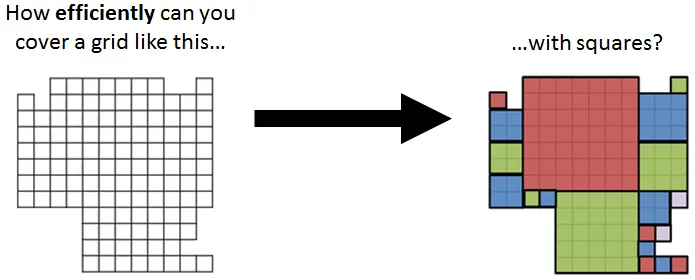
有一个明显的整数线性规划模型：生成所有可能的正方形（如果正方形仅覆盖存在的网格单元，则正方形是可能的），为每个正方形引入一个二进制变量x_i，指示我们是否使用它，然后

minimize sum x_i

subject to:
1) x_i is an integer
2) 0 ≤ x_i ≤ 1
3) for every cell c
       (sum[j | c ϵ square_j] x_j) = 1

约束条件3指每个单元格恰好被覆盖一次。约束条件1和2使x_i为二进制。最小解法可给出原问题的最优解。

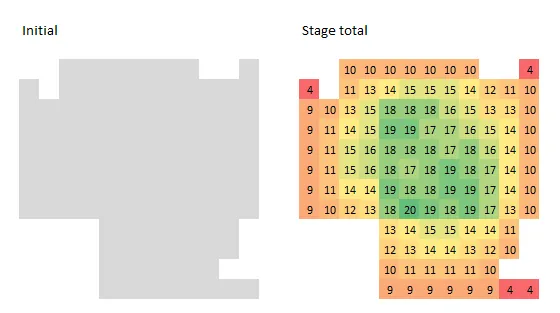
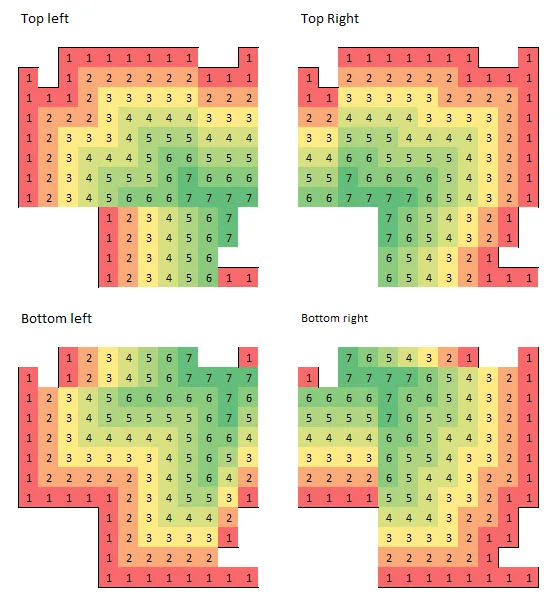
线性松弛（即忽略约束条件1）的表现还算不错，但它会做出这样的事情（这是一个6×6的网格，左上角缺失）：

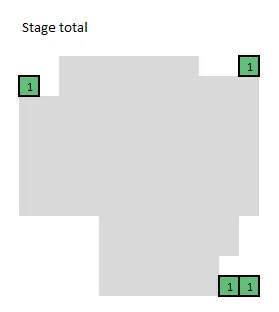
这里选择了13个正方形的“一半”（即客观值为6.5），并标明了它们的大小（以便更容易找到它们）

• 1个4x4的正方形
• 3个3x3的正方形
• 6个2x2的正方形
• 3个1x1的正方形

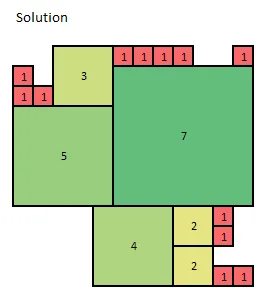
这种情况下的最优解的客观值为8，例如以下解：

线性松弛法还算不错，但我对它并不完全满意。间隙有时超过10％，有时会导致整数阶段非常缓慢。

这就是实际问题的关键所在，我能否添加额外的约束条件（作为割），以改善分数解？

我尝试了问题的另一种表述方式来找到割，例如，选择方块而不是左上角和右下角，然后将它们匹配起来形成覆盖所有单元格的非重叠方块。然后，在每个“反斜杠对角线”上，必须有相等数量的左上角和右下角匹配。但这没有帮助，因为如果我们选择正方形，则该条件始终为真，即使在分数解中也是如此。

我还尝试过一些关于重叠的推理，例如，如果两个正方形明显重叠，则它们的总和不能大于1，并且可以通过添加所有完全包含在重叠区域中的正方形来改进。但是，该约束比所有单元格仅被覆盖一次的约束不那么有力。

我尝试过关于总面积的推理（即总覆盖面积必须等于单元格数），但这已经由每个单元格必须被覆盖一次的约束保证，将其陈述为总面积只会增加自由度。

我也尝试过处理平方数（每个正方形的面积都是一个平方），以及平方数之间的差异，但这并没有带来任何有用的结果。

- harold

---

我不同意“范围过大”的标记，我只是特别地要求切割问题的解决方法，而不是高效的解决方法。 - harold

是的，“cut”是常见的LP术语。您是否愿意接受一个建议更强大的分支策略的答案？ - David Eisenstat

我没有通过这个问题。它在审核中被标记为审计。尽管如此，我仍然相信有其他更适合这个问题的网络。算法或与线性规划相关的东西可能更好？ - Ely

@Elyasin 在其他一些网站上，这个话题可能是相关的，但在这里并不是不相关的。 - David Eisenstat

我认为SO是关于编程问题的。OP询问如何优化解决方案。 - Ely

Answer 1

我曾在类似问题（ITA的“草莓地”；向下滚动）上使用分支和价格法取得了良好的效果。这是我的代码，由于缺少注释，可能只能作为零知识证明表明我知道自己在说什么。它比商业求解器（我不会透露名称）快几个量级。

关键是分支策略。与其直接在x_i变量上进行分支，这可能是您的求解器正在执行的操作，不如在更高级别的决策上进行分支。我用于草莓领域的策略是决定两个单元格是否被同一个正方形覆盖。如果您针对小数解最为犹豫的配对，那么解的结构似乎会很快确定。

很遗憾，我无法为您提供如何将此程序编程到现有整数程序求解器中的建议。对于Strawberry Fields，我选择了自定义的一切，主要是因为我想这样做，但部分原因是我正在即时生成列，使用累积网格行和网格列总和快速评估矩形。

- David Eisenstat

---

非常有趣，你能提供一些为什么它如此有效的见解吗？ - harold

@harold 禁止一个特定的方块并没有很大程度地改变放松值。 - David Eisenstat

Answer 2

目标函数值的约束

每当目标函数值为非整数时--例如，因为您在分数解中有奇数个0.5权重的正方形--您可以在"目标函数上直接添加割（cut）"来强制将其推至下一个更高的整数值：例如，在您的例子中，分数解具有13个正方形，每个正方形的权重为0.5，总目标函数值为6.5，您可以添加约束条件，使所有x_i的和>= 7。

更一般的割（cut）

这导致了一个更普遍的规则，无论何时您都有一个分数解，在该分数解中，某些单元格子集C被某些具有非整数权重w的正方形子集S"完全覆盖"。通过"完全覆盖"，我的意思是S中的正方形每个都有非零权重，并且对于C中的每个单元格，它们共同提供权重为1，并且不会与C之外的单元格重叠。您可以通过创建一个图，其中每个单元格都有一个顶点，每当它们由分数解中相同的正方形部分地覆盖时，它们之间就有一条边：此图的每个连通分量都是这样的（最小）子集。

在具有如上所述的一些确切覆盖单元格子集C和正方形子集S的分数解中，令T为仅重叠C中单元格的所有正方形的集合（显然，T是S的超集）。我们知道，任何最优解X都必须与S具有相同的总权重，其中LP子问题仅包含单元格子集C（和候选正方形子集T）：如果它没有，这将违反原始LP的分数解的最优性：您可以用X替换S并获得更好的解决方案。

现在，有两个解集（其中任一个可能为空）：那些不覆盖单元格C和C之外单元格的正方形，以及至少某些正方形覆盖了这两种单元格。我们希望禁止第一类解中的总体重量<RoundUp(w)。让U成为覆盖至少一个C内单元格和C外单元格的所有正方形的集合。我们可以通过添加约束条件来实现这一点。

Sum_{square_i in T}(x_i) + RoundUp(w) * Sum_{square_j in U}(x_j) >= RoundUp(w)

将LHS的第二项乘以RoundUp(w)的效果是，如果一个覆盖了C单元格和其他单元格的正方形被包含在解决方案中，那么约束条件有效地“消失”了。这是必要的，因为S和C并不能告诉我们关于原问题的这种解决方案的任何信息，因此我们不能排除它们。请注意，包含子集S的原始解决方案将被此约束禁止，因为U中的每个正方形在此解决方案中都必须具有重量0。

没有万能药

第二种方法比第一种更强大，因为可能会发生这样的情况，例如，图形包含两个组件，每个组件都有奇数个正方形，所有正方形的重量均为0.5：这意味着总共有偶数个正方形，这意味着总体目标函数值是整数，从而防止在目标函数上添加割。但是，即使再次应用这些割，也不能保证最终会找到可行的解决方案：具体来说，任何时候，网格本身在水平和/或垂直方向上对称但可以由不对称正方形集合覆盖时，它同样可以由该正方形集合的水平和/或垂直翻转版本以及这两个正方形集合的任何“仿射组合”（即，权重总和为1的任何组合）覆盖。一般来说，可能会有许多同样好的可行解，我描述的割并没有给出停止LP求解器返回包含所有k个解的“叠加”的解决方案的方法，其中所有正方形都被分配了重量1/k。

一个好消息！

虽然如我上面提到的，没有办法让LP求解器从多个对称最优覆盖的分数“叠加”中“隔离”一个特定的可行覆盖，但是有好消息：如果您确实得到了这样的叠加，那么从中恢复单个最优的可行覆盖实际上非常容易。您需要做的就是贪心地选择具有非零权重的正方形，每次划掉与您刚刚选择的正方形重叠的任何正方形。如果解决方案如我所描述的那样是叠加的，则保证可以工作，而且同样重要的是：如果此过程在分数解决方案上有效（也就是说，如果重复此贪心步骤最终覆盖了所有单元格），则您获得的解决方案必须是最优的！（假设它不是：让X是LP求解器返回的最优分数解，让F是您从中贪心提取的可行解决方案，并让y是F中任何正方形的最小权重。请注意，F中的每个正方形都会为每个单元格的覆盖值贡献至少y；因此，由于假设F是次优的，将F中每个正方形的权重减去y并将X中所有其他权重放大1 /（1-y）将给出另一个（可能再次是分数）的解决方案，其重量较低，这与X的最优性相矛盾。）

证明任何分数解要么（i）在“覆盖图”中有非整数总权重的某个组成部分，要么（ii）由这样的叠加组成：这意味着您可以继续应用我的“通用”割，直到得到一个叠加，然后您可以贪心地解决它。但是目前为止，可能存在不属于这两个类别的分数解。

- j_random_hacker

---

非常好，它运行得非常顺畅，而且这正是我要求的，所以我授予你赏金。 - harold

很高兴听到这个 :) 如果你遇到所谓的“第三类”分数解，即非整数解的仿射组合不是整数解的仿射组合，我会很感兴趣知道。 - j_random_hacker

我还不确定，我有一些实例怀疑属于第三类，但它们太大了无法手动检查，而且我也不完全信任我的检查实现。 - harold

我又想到了一件事：尽管贪心可行解提取算法是正确的，因为如果它找到一个可行的覆盖，那么这个覆盖必须是最优的，但很有可能它无法完成覆盖，即使一个可行的覆盖在分数解中潜伏着。（例如，一个3x2的网格可以用两种方式最优地覆盖：使用一个2x2块和两个1x1块，以及相同的但沿着较长轴翻转。如果给出这些的叠加，如果贪心算法恰好先选择3个1x1块，它将无法覆盖所有单元格。）... - j_random_hacker

为确保始终找到任何潜在的覆盖，您需要在具有分数解中非零权重的正方形中寻找[EDITED]最小大小的最大独立集（将这些正方形想象为顶点，边连接重叠的正方形）。 这是NP难问题，但除非存在大量重合的解，否则应该很快。 当然，您可以在O（3 ^（n / 3））时间内枚举所有最大IS，这对于n <= 50应该是可行的。 - j_random_hacker

啊，当然，那有点烦人 :) 到目前为止，使用普通的整数线性规划求解器解决最终问题效果很好，所以我可以这样做。 - harold

Answer 3

我会使用类似 A* 的搜索来找到解决方案。需要注意的是，A* 类似于 贪婪最佳优先搜索，可以使用启发式方法来指导自己。假设您有一个正确的启发式方法，它将在合理的时间内找到接近最优（~0.95）的解决方案。

示例解决方案使用了18个块，而不是示例中显示的19个块。除了启发式，您还可以使用一些预计算来增加算法的有效性。例如，我为每个位置计算了所谓的自由梯度。例如，您的初始地图变成一个阶段：

你可以拥有自己的启发式算法，其效果可能同样好甚至更好。我只是因为发现它很琐碎才使用了这个算法。阶段编号具有以下含义：数字越高，越可能出现在大箱子中（你可以得出更多的限制条件，但这只是一个开始）。

阶段值是4个地窖自动化规则的总和。

例如 左上角。

cell(x,y) := min(cell(x,y-1) ?? 0, cell(x-1,y) ?? 0, cell(x-1,y-1) ?? 0) + 1

?? 运算符被称为空值合并运算符。如果左操作数不为 null ，它将返回左操作数；否则返回右操作数。

---

另外，您可以通过从预计算中获取的已知解决方案来减少所需的计算工作，并在每个阶段进行。 在这种情况下，状态为0：

算法本身会重复执行以下步骤：

1. 对单元格进行排序，并取最高值
2. 对自动化规则结果进行排序，并取最高值
3. 查找微不足道的截止点

---

如果您想要在更大的网格中获得更快的结果，那么一个比较直接的方法就是将预计算扩展到编译模板。之后可以进行模板简化。

例如，您可以拥有一个模板（左上部分）。

--+++
+-+++
+++++

你可以生成它的哈希值，并将其添加到哈希表/字典中，值为4（表示最少需要4个矩形来覆盖'+'）。然后你有一个5x3的范围，使用相同的哈希值，你知道这是一种成本为4的平凡截止方式。

之所以更快，是因为与计算近似恒定速度的哈希相比，比较需要很长时间。

---

另外，有一种方法可以催眠我们是否正在寻找解决方案以及何种类型的解决方案。使用 Wolfram Mathematica 函数 FindMinimum，它看起来应该是这样的：

FindMinimum[{
  a + b + c + d + e + f + g, 
  (a 1^2 + b 2^2 + c 3^2 + d 4^2 + e 5^2 + f 6^2 + g 7^2) == 119 &&
  a >= 0 && b >= 0 && c >= 0 && d >= 0 && e >= 0 && f >= 0 && g >= 0 &&
  a \[Element] Integers &&
  b \[Element] Integers &&
  c \[Element] Integers &&
  d \[Element] Integers &&
  e \[Element] Integers &&
  f \[Element] Integers &&
  g \[Element] Integers
}, {a,b,c,d,e,f,g}]

这基于一个假设，即我们有一个12x12的网格，有119个单元，这将为我们提供使用网格大小计数的最佳解决方案。

不幸的是，wolfram alpha搜索引擎无法解释此内容，也许将来会有所改进。

- Margus

---

这很有趣，但我不认为它真正回答了我的问题。 - harold

这非常好，类似于我提到使用启发式方法选择下一个要移除的单元格，并删除具有单一可能覆盖的单元格。 - gen-y-s

Answer 4

动态规划：选择一个单元格（任何单元格都可以），计算所有有效的覆盖它的正方形（即只覆盖当前单元格和网格中其他单元格）。对于每个这样的正方形，递归获取剩余区域（网格减去正方形）的最小覆盖值，然后从中选择最小值（结果为该值+1）。 为了加快速度，在每个递归级别中尽量选择具有最少有效覆盖正方形的单元格（从而减少每个级别中的递归调用次数）。

很简单。

- gen-y-s

---

这需要时间复杂度为O(2^n)和空间复杂度，对于包含n个网格单元的输入，因为您需要计算并存储剩余网格单元的每个连接子集的最优解，所以在超过大约25个单元的输入上可能不可行。 - j_random_hacker

是的，最大空间是2^n，但如果您使用合理的启发式算法（比如选择沿区域边缘的单元格），实际需要计算的部分区域数量可能远少于n^2。您可以将其存储在哈希表中。 - gen-y-s

那么我们可以有多少种方法呢？与将高度为k的线分成任意数量（整数长度）的部分相同。对此的递归是f(0) = 1，f(k>0) =从i = 0到k-1的总和f(i)。很容易看出f(k) = 2^(k-1)。因此，例如，如果一个大小为10的正方形适合左下角的单元格，则有512种不同的覆盖方式 只是这个正方形的左边缘用较小的正方形 - 显然，一旦包括更多正方形，涉及更多子问题。 - j_random_hacker

责任在于您展示比O(2^n)更好的界限，例如通过证明我列出的许多子问题不可能出现。这将是困难的：虽然我的子问题集中有部分解决方案（方块堆），确实可能不会出现在您的分支策略中（例如，每当我们有一个方块堆，其中顶部方块X大于下面的方块Y，并且剩余未覆盖的高度大于Y的高度时，您的方法将尝试覆盖Y右侧的某个方块... - j_random_hacker

...... (或一些较低的正方形)，而我的算法将继续尝试覆盖X上方最左边的正方形，但是将高为k的线段分成任意数量的非递增整数长度的线段的任何方法都会导致子问题，其中我将选择要覆盖的下一个单元格恰好是由最少数量的正方形覆盖的单元格，因此这样做的方式的数量为您的策略提供了有效的下限。 由于这些被分区号计数，这些号码渐近地为1 /（4sqrt（3）n）\ * e ^（pi \ * sqrt（2n / 3）），因此子问题的数量增长快于k中的任何多项式。 - j_random_hacker

Answer 5

如何使用一个限制条件，使正方形的总面积等于需要覆盖的总面积，除了禁止重叠的约束条件？这比检查双重覆盖约束条件要快。

- gen-y-s

---

这已经被限制条件所暗示，即每个单元格都被一个重量为1的权重覆盖。 - harold

是的，我只是觉得使用总和约束会更快，而不是“每个单元格都被1覆盖”（也就是没有重复覆盖）的约束。 - gen-y-s

这确实会显著减少约束的数量，但除非您懒惰地回去添加常规约束，否则它也会增加整数间隙。 - harold