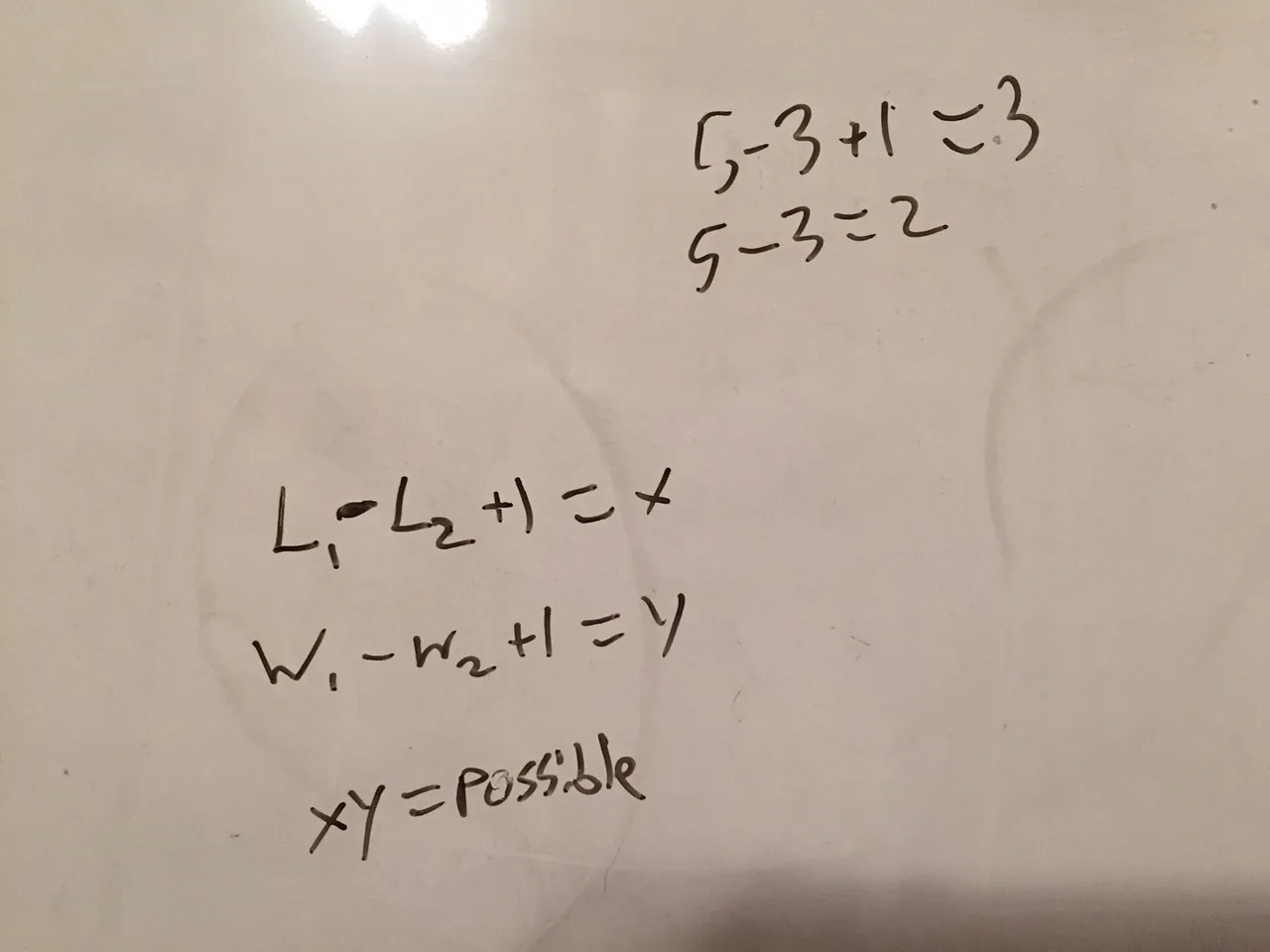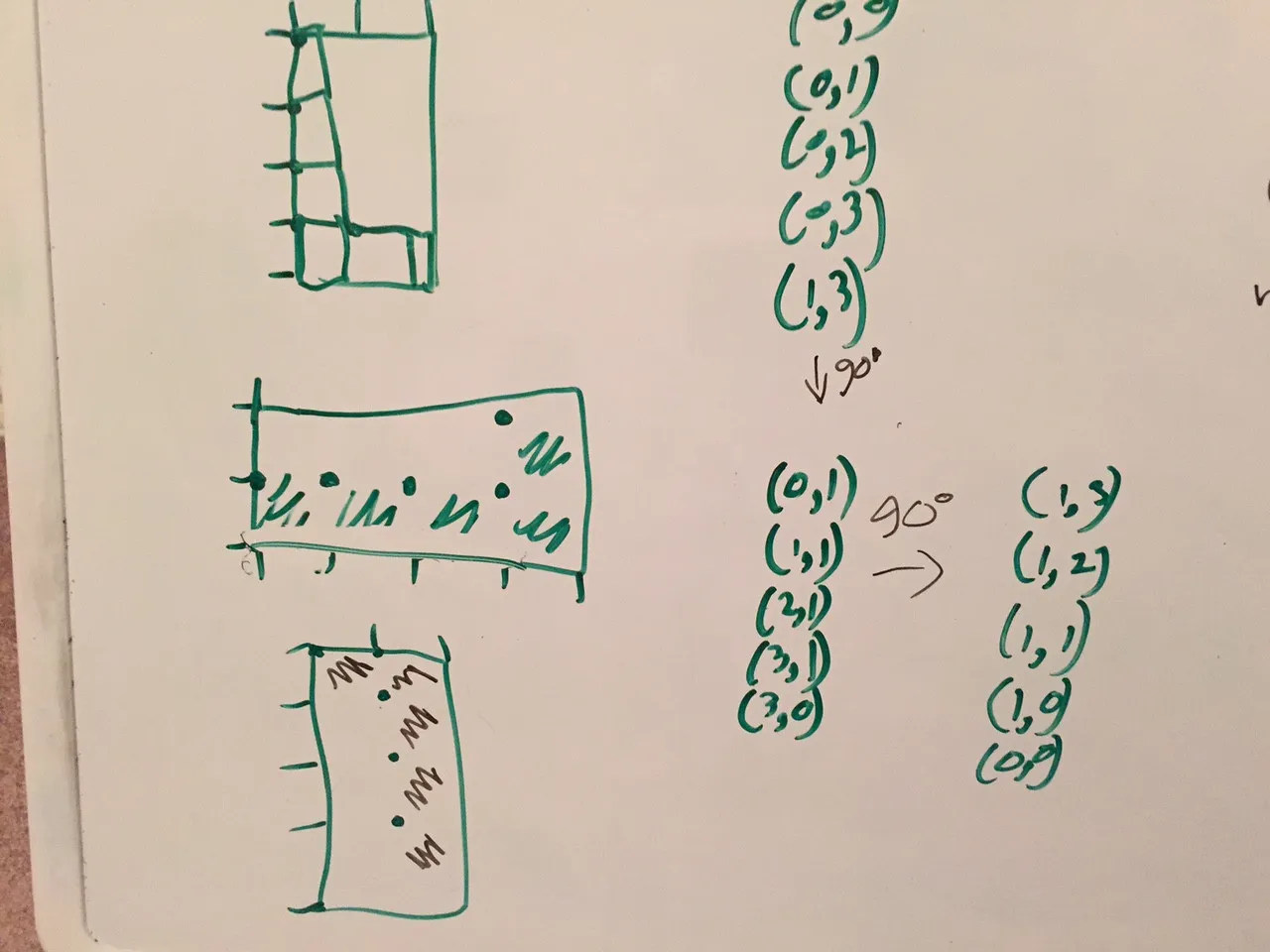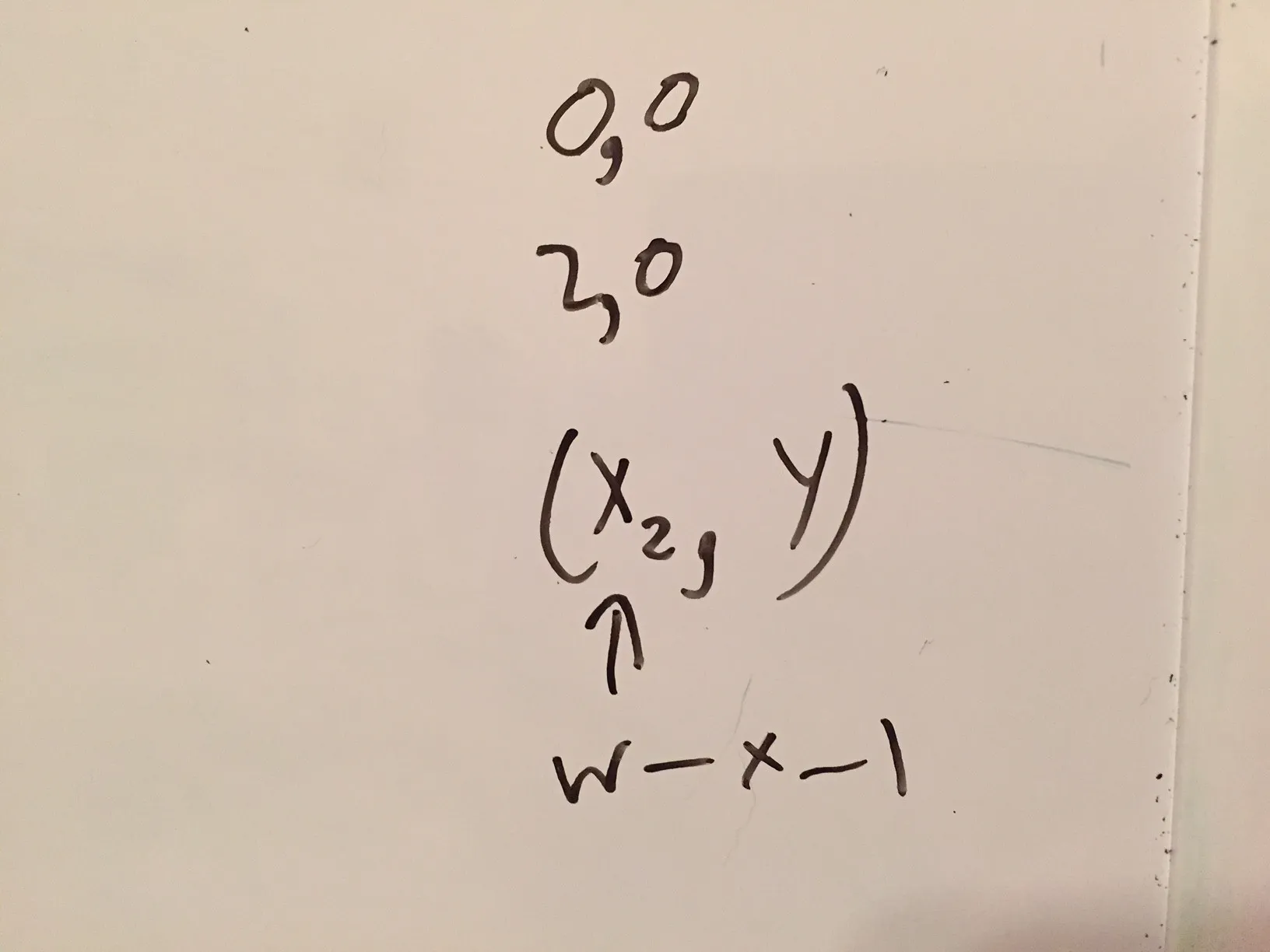我已经工作了几天,最终决定在这里发布我的问题。我将详细解释我正在做什么以及如何进行。
在继续之前,我查阅了维基百科和其他20个解释此问题的网站,但这并没有帮助我。
链接1:Dancing Links - 维基百科 链接2:Knuth的算法x。 其中一个更有用的网站:链接3:Kanoodle,但是当涉及到我的问题时,解释非常差。
问题:如何用W、I和L形五格拼图覆盖5xn的矩形?您可以翻转和旋转它们。你可能会问什么是五格拼图?五格拼图由五个方块组成,共同构建一个图形。例如W形五格拼图。
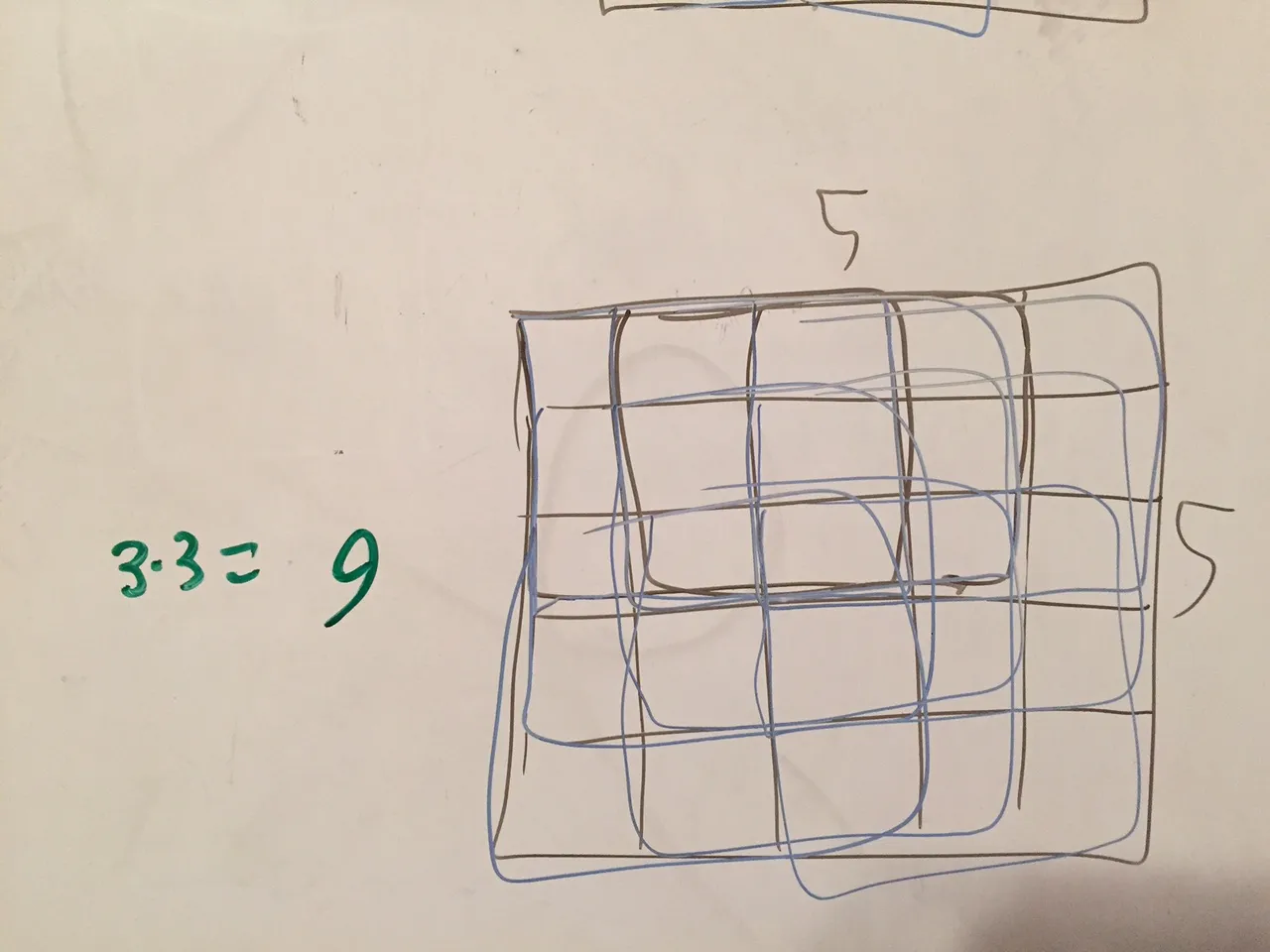
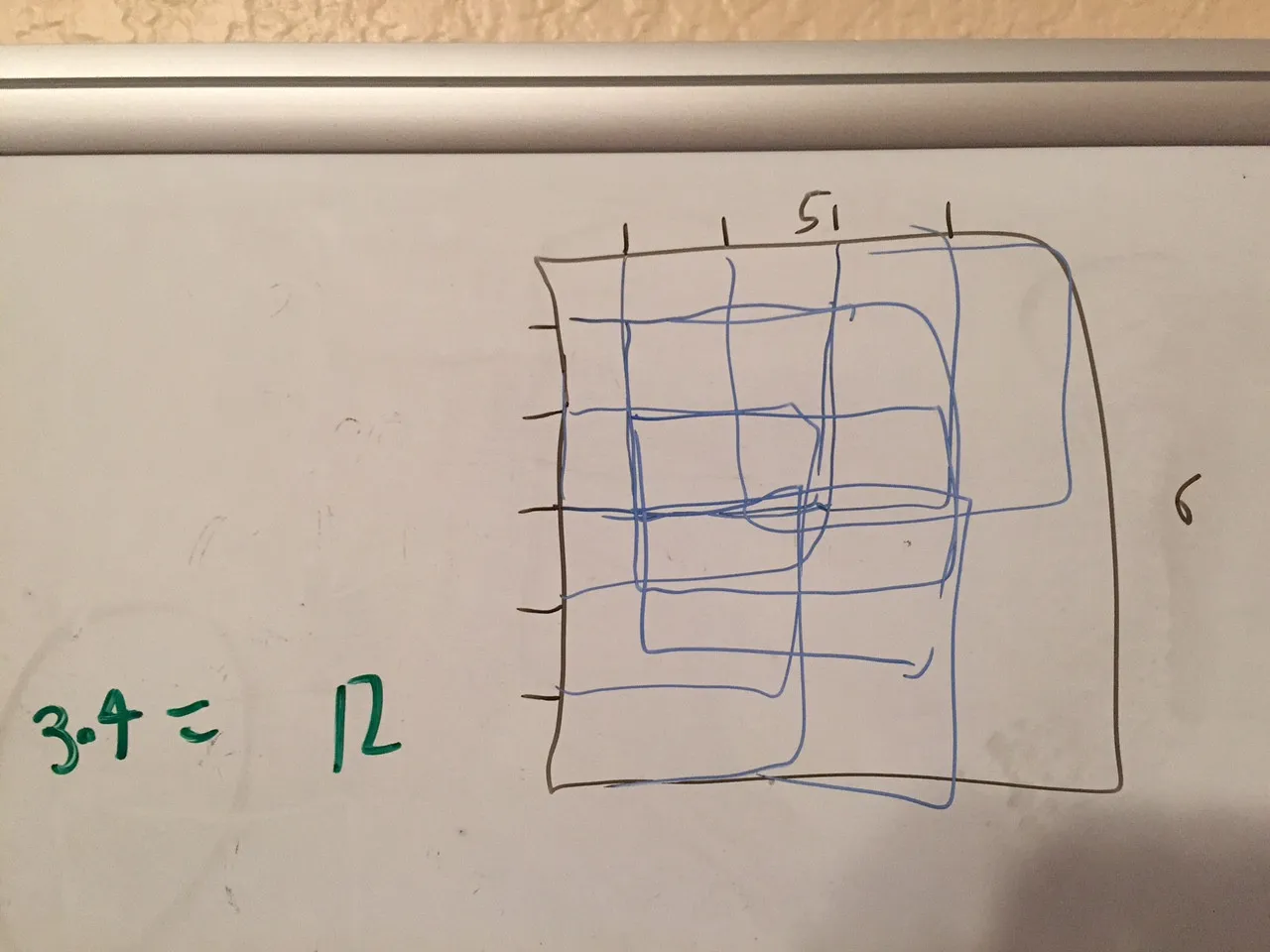
不是在5xn的场地上实现W、L和I型五格方块,我简化了任务,开始思考在5x3的场地中填充"W"的所有可能方法。 就像这样。 我的下一步是思考一个矩阵,它看起来类似于Knuth的DLX算法,我得到了这个。黄色和橙色之间的绿线意味着您可以将两者放在一起以获得另一个有效的解决方案。我的下一个文本描述了这条绿线。
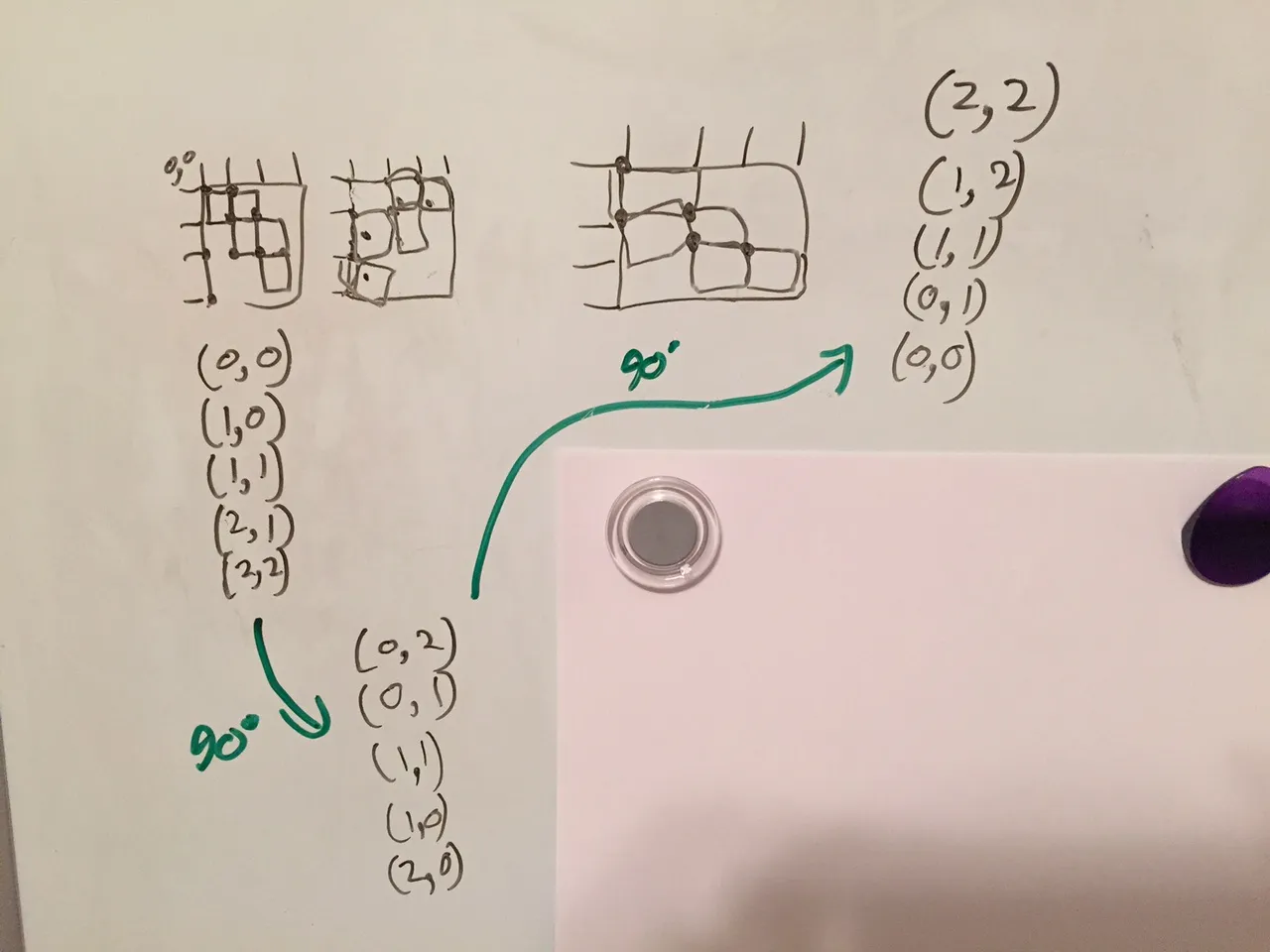
我的下一步是思考一个矩阵,它看起来类似于Knuth的DLX算法,我得到了这个。黄色和橙色之间的绿线意味着您可以将两者放在一起以获得另一个有效的解决方案。我的下一个文本描述了这条绿线。
 我注意到,如果我取一行并检查该行下面或上面的任何其他行是否在同一列中没有1,则我有一个有效的解决方案。但我不知道如何实现它。经过数小时的研究,我找到了另一种描述我的问题的方法。我取了一个子集(我的W型五格方块)并将其定义为这样。
我注意到,如果我取一行并检查该行下面或上面的任何其他行是否在同一列中没有1,则我有一个有效的解决方案。但我不知道如何实现它。经过数小时的研究,我找到了另一种描述我的问题的方法。我取了一个子集(我的W型五格方块)并将其定义为这样。
 再次遇到了实现难题。
再次遇到了实现难题。
链接1:Dancing Links - 维基百科 链接2:Knuth的算法x。 其中一个更有用的网站:链接3:Kanoodle,但是当涉及到我的问题时,解释非常差。
问题:如何用W、I和L形五格拼图覆盖5xn的矩形?您可以翻转和旋转它们。你可能会问什么是五格拼图?五格拼图由五个方块组成,共同构建一个图形。例如W形五格拼图。
| A | B | C
---------------
a | 1 | 0 | 0 |
-------------
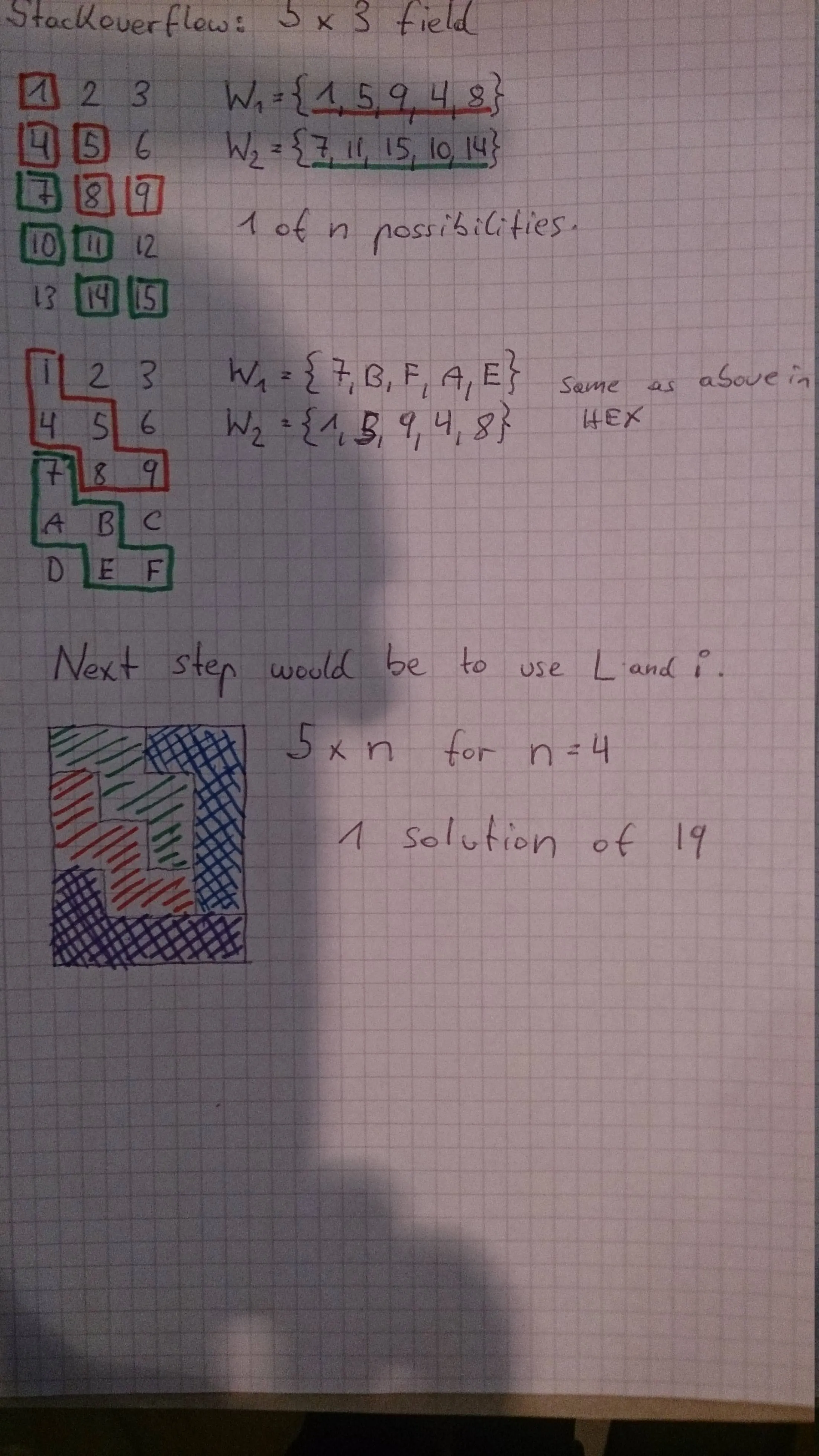
b | 1 | 1 | 0 | Imagine all the 1s together they build a big "W".
------------- If you look at my picture it will be clearer.
c | 0 | 1 | 1 |
不是在5xn的场地上实现W、L和I型五格方块,我简化了任务,开始思考在5x3的场地中填充"W"的所有可能方法。 就像这样。
 我的下一步是思考一个矩阵,它看起来类似于Knuth的DLX算法,我得到了这个。黄色和橙色之间的绿线意味着您可以将两者放在一起以获得另一个有效的解决方案。我的下一个文本描述了这条绿线。
我的下一步是思考一个矩阵,它看起来类似于Knuth的DLX算法,我得到了这个。黄色和橙色之间的绿线意味着您可以将两者放在一起以获得另一个有效的解决方案。我的下一个文本描述了这条绿线。
 我注意到,如果我取一行并检查该行下面或上面的任何其他行是否在同一列中没有1,则我有一个有效的解决方案。但我不知道如何实现它。经过数小时的研究,我找到了另一种描述我的问题的方法。我取了一个子集(我的W型五格方块)并将其定义为这样。
我注意到,如果我取一行并检查该行下面或上面的任何其他行是否在同一列中没有1,则我有一个有效的解决方案。但我不知道如何实现它。经过数小时的研究,我找到了另一种描述我的问题的方法。我取了一个子集(我的W型五格方块)并将其定义为这样。
 再次遇到了实现难题。
再次遇到了实现难题。
所以这是我的问题:你会如何在JAVA中实现这个问题?我的方法好吗?你能接受我的想法吗?如果可以,你会怎么做?如果不行,你能告诉我我的思路出了哪些问题吗?
这是给我的代码。
package data;
public class PentominoWILDLX
{
static Node h; // header element
static int cnt; // count solutions
public PentominoWILDLX()
{
h = new Node(); // init header element
cnt = 0; // init counter
}
public static void search (int k) // finds & counts solutions
{
if(h.R == h) // if empty: count & done
{
cnt++; return; // choose next column c
}
Node c = h.R; // remove c from clumns
cover(c); // choose next colun c
for (Node r=c.D; r!=c; r=r.D) // forall rows with 1 in c
{
for(Node j=r.R; j!=r; j=j.R) // forall 1-elements in row
{
cover(j.C); // remove clumn
}
search(k+1); // recursion with k+1 << hier überpfüen ob ich ändern muss
for (Node j=r.L; j!=r; j=j.L) // forall 1-elemnts in row
{
uncover(j.C); // backtrack . unremove? << googlen
}
uncover(c); // unremove f c to coulmns
}
}
public static void cover (Node c) // remove clumn c
{
c.R.L = c.L; // remove header
c.L.R = c.R; // from row list
for (Node i=c.D; i!=c; i=i.D) // forall rows with 1
{
for (Node j=i.R; i!=j; j=j.R) // forall elem in row
{
j.D.U = j.U; // rmove row elemnt
j.U.D = j.D; // from column list
}
}
}
public static void uncover (Node c) // undo remove col c
{
for (Node i=c.U; i!=c; i=i.U) // forall rows with 1
{
for (Node j=i.L; i!=j; j=j.L) // for all elem in row
{
j.D.U = j; // unremove row ele,
j.U.D = j; // to lumn list
}
c.R.L = c; // unremove header
c.L.R = c; // to row list
}
} // end of class
class Node // represents 1 element or header
{
Node C; // reference to column-header << h?,
Node L; // left
Node R; // right
Node U; // reference up
Node D; // down reference down
Node()
{
C=L=R=U=D=this; // 2*double-linked circular list
}
} // end of class
public static void main(String[] args)
{
}
}