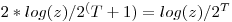连续着色分形图像

Question

我正在尝试使用OpenGL可视化Mandelbrot集，并发现在平滑着色方面存在非常奇怪的行为。

假设对于当前的复数值C，算法在Z被证明大于2时逃脱了n次迭代。

我编写了以下颜色部分的程序：

if(n==maxIterations){
   color=0.0; //0.0 is black in OpenGL when put to each channel of RGB 
              //Points in M-brot set are colored black.
} else {
   color = (n + 1 - log(log(abs(Z)))/log(2.0) )/maxIterations; 
   //continuous coloring algorithm, color is between 0.0 and 1.0
   //Points outside M-brot set are colored depending of their absolute value,
   //from brightest near the edge of set to darkest far away from set.
}
glColor3f(color ,color ,color );
//OpenGL-command for making RGB-color from three channel values. 

问题是，这并不起作用。一些平滑处理是可以注意到的，但并不完美。

但是当我添加两个额外的迭代时（在某个地方找到这个方法而没有解释）

Z=Z*Z+C; 
n++; 

在计算颜色之前的“else”分支中，图片变得非常平滑和优美。

为什么会这样呢？为什么我们需要在检查点是否位于集合中之后，在着色部分添加额外的迭代次数？

- fyodorananiev

---

只是出于好奇，那是什么语言？我想知道这是因为它似乎有一个处理复数的abs()函数。 - Jonas Elfström

这是Visual C++。代码使用Visual C++的<complex>类编写。在此处检查：http://msdn.microsoft.com/en-us/library/0352zzhd.aspx - Fyodor

Answer 1

我并不确定，但我猜测这可能与一个数字的对数的对数(log(log(n)))对于“小”数字n而言是不稳定的有关系，其中“小”的含义接近2。如果你的Z刚逃逸出来，它就接近2。如果你继续迭代，你会越来越远离2，并且log(log(abs(Z)))稳定下来，从而给出更可预测的值......然后给出更平滑的值。

任意选择的示例数据:

 n            Z.real            Z.imag         |Z|  status color
-- ----------------- ----------------- ----------- ------- -----
 0             -0.74              -0.2    0.766551 bounded [nonsensical]
 1           -0.2324             0.096    0.251447 bounded [nonsensical]
 2       -0.69520624        -0.2446208    0.736988 bounded [nonsensical]
 3    -0.31652761966     0.14012381319    0.346157 bounded [nonsensical]
 4    -0.65944494902    -0.28870611409    0.719874 bounded [nonsensical]
 5    -0.38848357953     0.18077157738    0.428483 bounded [nonsensical]
 6    -0.62175887162    -0.34045357891    0.708867 bounded [nonsensical]
 7    -0.46932454495     0.22336006613    0.519765 bounded [nonsensical]
 8    -0.56962419064    -0.40965672279    0.701634 bounded [nonsensical]
 9    -0.58334691196     0.26670075833    0.641423 bounded [nonsensical]
10     -0.4708356748    -0.51115812757     0.69496 bounded [nonsensical]
11    -0.77959639873     0.28134296385    0.828809 bounded [nonsensical]
12     -0.2113833184    -0.63866792284     0.67274 bounded [nonsensical]
13     -1.1032138084    0.070007489775     1.10543 bounded 0.173185134517425
14     0.47217965836    -0.35446645882    0.590424 bounded [nonsensical]
15    -0.64269284066    -0.53474370285    0.836065 bounded [nonsensical]
16     -0.6128967403     0.48735189882    0.783042 bounded [nonsensical]
17    -0.60186945901    -0.79739278033    0.999041 bounded [nonsensical]
18     -1.0135884004     0.75985272263     1.26678 bounded 0.210802091344997
19    -0.29001471459     -1.7403558114     1.76435 bounded 0.208165835763602
20     -3.6847298156     0.80945758785     3.77259 ESCAPED 0.205910029166315
21      12.182012228     -6.1652650168     13.6533 ESCAPED 0.206137522227716
22      109.65092918     -150.41066764     186.136 ESCAPED 0.20614160700086
23     -10600.782669     -32985.538932     34647.1 ESCAPED 0.20614159039676
24     -975669186.18       699345058.7 1.20042e+09 ESCAPED 0.206141590396481
25  4.6284684972e+17 -1.3646588486e+18 1.44101e+18 ESCAPED 0.206141590396481
26 -1.6480665667e+36  -1.263256098e+36 2.07652e+36 ESCAPED 0.206141590396481

请注意，在n [20,22] 时颜色值仍在波动，n = 23 时变得稳定，并且从n = 24 开始保持一致。请注意，那里的Z值远远超出了界限曼德博集合的半径2圆圈。

我实际上还没有做足够的数学工作来确信这是否是一个可靠的解释，但这应该是我的猜测。

- lindes

---

我应该指出，我并不确定这是否是导致这种情况的原因。经过检查其他数字后，我所说的关于持续迭代稳定性的部分是准确的，但是一个点的第一次逃逸值和另一个附近点的第一次逃逸值之间的差异似乎并不比五次迭代后逃逸值之间的差异更大。但也许我只是使用了评估非常相似的点？我必须更深入地探索才能确定。 - lindes

Answer 2

我刚刚写了同样的程序，作为一个优秀的数学家，我会解释一下为什么，希望能够清楚明白。

如果假设种子C的序列在k次迭代后逃逸。

由于函数本身被定义为极限，随着迭代次数趋近于无穷大，得到接近k的结果并不好。原因如下。

由于我们知道在2之后，序列会变成无穷大，让我们考虑一些迭代T，在那里z已经变得足够大。相对于它来说，C将变得微不足道地小，因为通常你在[-2,2]和[-1.5,1.5]的2个轴上查看集合。因此，在T+1次迭代中，z将是前面的z^2，很容易检查在这种情况下|z| T+1将是前面|z|^2的近似值。

我们的函数是 log(|z|)/2^k，其中 k 表示第 k 次迭代。在我们需要考虑的情况下，很容易看出在第 T+1 次迭代中它将变为 ~~

_{(来源：equationsheet.com)}

这就是第 T 次迭代的函数。

换句话说，当 |z| 变得比种子 C "显著"更大时，函数会变得越来越稳定。您不想使用接近逃逸迭代 k 的迭代，因为在那里实际上 Z 将接近 2，而根据 C 的不同，它可能与 C 相比并不显着小，因此您将离极限较远。

当 |C| 接近 2 时，在第一次逃逸迭代中，您将离极限相差很远。另一方面，如果您选择在 |Z|>100 上进行逃逸边界，或者只是多迭代几次，您将获得更加稳定的结果。

希望任何对这个问题感兴趣的人都能得到良好的答案。

- Alex Botev

Answer 3

目前看来，“迭代次数增加”的想法没有令人信服的公式，除非考虑到它确实起作用。

在维基百科曼德博集合的一个旧版本文章中有连续着色的相关内容：

其次，建议进行一些额外的迭代，以便 z 可以增长。如果您停止迭代并让 z 逃脱，那么平滑算法可能无法正常工作。

总比没有好。

- fyodorananiev