我最近在职面试中被问到的一个问题是:
Write a data structure that supports two operations.
1. Adding a number to the structure.
2. Calculating the median.
The operations to add a number and calculate the median must have a minimum time complexity.
我的实现非常简单,基本上是保持元素排序,这样添加一个元素的成本为O(log(n))而不是O(1),但中位数是O(1)而不是O(n*log(n))
我还添加了一个朴素的实现,但其中包含了一个numpy数组中的元素:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from random import randint, random
import math
from time import time
class MedianList():
def __init__(self, initial_values = []):
self.values = sorted(initial_values)
self.size = len(initial_values)
def add_element(self, element):
index = self.find_pos(self.values, element)
self.values = self.values[:index] + [element] + self.values[index:]
self.size += 1
def find_pos(self, values, element):
if len(values) == 0: return 0
index = int(len(values)/2)
if element > values[index]:
return self.find_pos(values[index+1:], element) + index + 1
if element < values[index]:
return self.find_pos(values[:index], element)
if element == values[index]: return index
def median(self):
if self.size == 0: return np.nan
split = math.floor(self.size/2)
if self.size % 2 == 1:
return self.values[split]
try:
return (self.values[split] + self.values[split-1])/2
except:
print(self.values, self.size, split)
class NaiveMedianList():
def __init__(self, initial_values = []):
self.values = sorted(initial_values)
def add_element(self, element):
self.values.append(element)
def median(self):
split = math.floor(len(self.values)/2)
sorted_values = sorted(self.values)
if len(self.values) % 2 == 1:
return sorted_values[split]
return (sorted_values[split] + sorted_values[split-1])/2
class NumpyMedianList():
def __init__(self, initial_values = []):
self.values = np.array(initial_values)
def add_element(self, element):
self.values = np.append(self.values, element)
def median(self):
return np.median(self.values)
def time_performance(median_list, total_elements = 10**5):
elements = [randint(0, 100) for _ in range(total_elements)]
times = []
start = time()
for element in elements:
median_list.add_element(element)
median_list.median()
times.append(time() - start)
return times
ml_times = time_performance(MedianList())
nl_times = time_performance(NaiveMedianList())
npl_times = time_performance(NumpyMedianList())
times = pd.DataFrame()
times['MedianList'] = ml_times
times['NaiveMedianList'] = nl_times
times['NumpyMedianList'] = npl_times
times.plot()
plt.show()
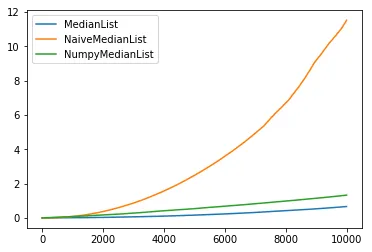
以下是10^4个元素的性能表现:
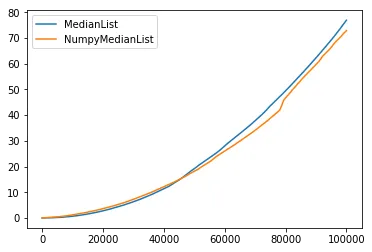
而对于10^5个元素,朴素的NumPy实现实际上更快:
我的问题是: 为什么?即使NumPy是通过一个常数因子加速的,如果它们没有保留排序后的版本,它们的中值函数如何扩展得这么好?