程序的时间复杂度使用递归方程。

Question

我想通过递归方程计算程序的时间复杂度。

这就是。。。

int f(int x)
{
if(x<1) return 1;
 else  return f(x-1)+g(x); 
}
int g(int x)
{
if(x<2) return 1;
 else return f(x-1)+g(x/2);
}

我写出了它的递归方程并尝试解决它，但它变得越来越复杂。

T(n) =T(n-1)+g(n)+c
         =T(n-2)+g(n-1)+g(n)+c+c
         =T(n-3)+g(n-2)+g(n-1)+g(n)+c+c+c
         =T(n-4)+g(n-3)+g(n-2)+g(n-1)+g(n)+c+c+c+c
         ……………………….
        ……………………..
        Kth time …..
        =kc+g(n)+g(n-1)+g(n-3)+g(n-4).. .. . … +T(n-k)

Let at kth time input become 1
Then n-k=1
         K=n-1
Now i end up with this..
T(n)= (n-1)c+g(n)+g(n-1)+g(n-2)+g(n-3)+….. .. g(1)

我无法进一步解决这个问题。无论如何，如果我们计算此程序中函数调用的次数，就可以很容易地看出时间复杂度是指数级的，但我想用递归来证明它。怎么做呢？

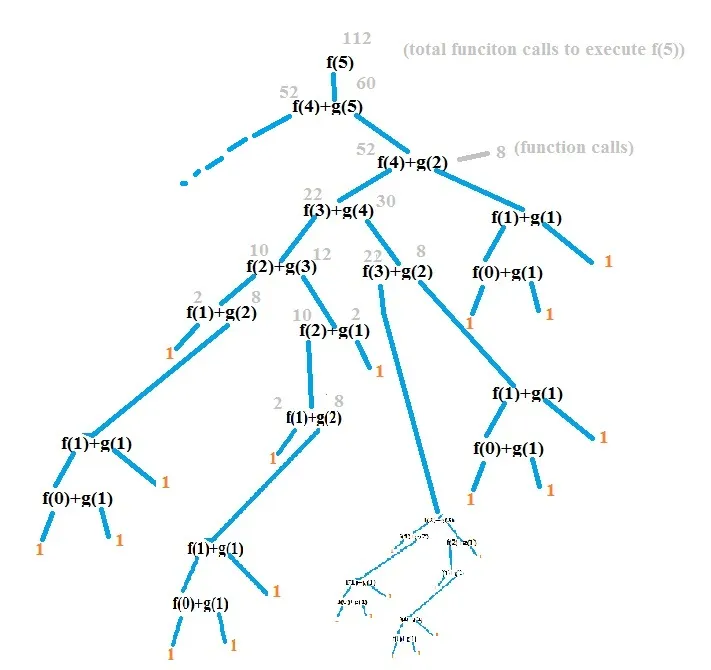
答案1中的解释看起来正确，我做过类似的工作。

这段代码中最困难的任务是编写递归方程。我画了另一个图表，发现了一些模式，我认为我们可以从这个图表中得到一些帮助，找出可能的递归方程。

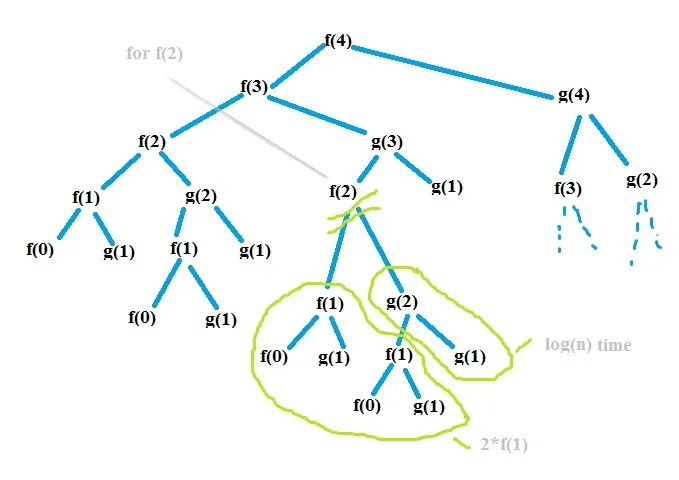
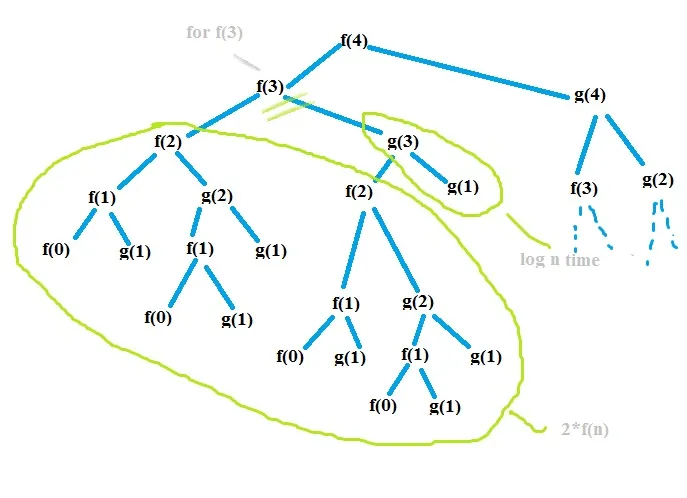
And I came up with this equation , not sure if it is right ??? Please help.

T(n) = 2*T(n-1) + c * logn

- siddstuff

---

你的确切问题是什么？你想证明 T_f(x) = Theta(c^x) 对于某个 c > 1 吗？还是你想要一个精确的公式？g 的情况也一样吗？ - Knoothe

这段代码非常令人困惑，我们需要同时考虑函数 f(x) 和 g(x)。 - siddstuff

你需要解决 g(x) = 2g(x - 1) - g((x - 1) / 2) + g(x / 2)，然后将其代入 f(x) 中以解决 f(x)。 - nhahtdh

@nhahtdh，你从哪里得到那个方程式的？ - Ed Rowlett-Barbu

@Zadirion：从关系式f(x) = f(x - 1) + g(x)和g(x) = f(x - 1) + g(x/2)可以得到一些推导。g(x) = f(x - 1) + g(x/2) = f(x - 2) + g(x - 1) + g(x/2) = g(x - 1) - g((x - 1)/2) + g(x - 1) + g(x/2)。（虽然我不知道如何解决这个问题）。 - nhahtdh

@sidstuff：胜者是谁呢……？Knoothe先生给出了最紧密的界限，他的答案值得被接受，在我看来，尽管我同意Saeed的观点，即2^n和3^n之间没有太大的实际差异。请不要告诉我们你的老师（这是作业，对吧？）说O(n)是答案（虽然……那我就赢了 :-) 顺便说一句：我很喜欢这个问题和讨论，先生们！ - Hans Lub

Answer 1

好的，我认为我已经能够证明f(x)=Theta(2^x)了（请注意时间复杂度是相同的）。这也证明了g(x)=Theta(2^x)，因为f(x)>g(x)>f(x-1)。

首先，正如大家所指出的那样，证明f(x)=Omega(2^x)很容易。

现在我们有关系式f(x) <= 2 f(x-1) + f(x/2)（因为f(x)>g(x)）。

我们将展示，对于足够大的x，存在某个常数K>0，使得 f(x) <= K*H(x)，其中H(x)=(2+1/x)^x 这意味着f(x)=Theta(2^x)，因为H(x)=Theta(2^x)，这本身可以从以下事实推出：H(x)/2^x->sqrt(e) as x->infinity（极限的wolfram alpha链接）。

现在（警告：更重的数学内容，也许更适合cs.stackexchange或math.stackexchange）。

根据wolfram alpha（点击链接并查看x = infinity附近的级数展开式）， H(x)=exp(x ln(2) + 1/2 + O(1/x)) 然后，再次根据wolfram alpha（点击链接（与上面不同）并查看x = infinity的级数展开式），我们有 H(x)-2H(x-1)=[1/2x + O(1/x^2)]exp(x ln(2) + 1/2 + O(1/x)) 所以 [H(x)-2H(x-1)]/H(x/2)->infinity as x->infinity 因此，对于足够大的x（比如x > L），我们有以下不等式： H(x) >= 2H(x-1) + H(x/2) 现在有一些K（仅依赖于L，例如K = f(2L)），使得： f(x) <= K*H(x) for all x <= 2L 现在我们通过（强）归纳法进行证明（如果需要可以转换成自然数） f(x+1) <= 2f(x) + f((x+1)/2) 归纳假设右边为 <= 2*K*H(x) + K*H((x+1)/2) 并且我们之前已经证明了 2*H(x) + H((x+1)/2) <= H(x+1) 因此，f(x+1) <= K * H(x+1)

- Knoothe

---

@Saeed 快点啊！我们所有的证明都使用相同的递归式 H(n) = 2H(n-1) + H(n/2)（我甚至计算了加法，作为一个一直注重成本的荷兰人...）你和我只差一步就能证明 O(2^n)。Knoothes 聪明的想法是使用级数 (2+1/n)^n，显然（在我擦亮眼镜后 :-)）是 O(2^n)。 - Hans Lub

(2+ε)^n使用一个“固定”的ε，这将不会得到O(2^n)。而(2+1/n)^n使用一个“递减”的ε，并获得了结果。 - Hans Lub

@SaeedAmiri：顺便说一下，这个证明的核心是 H(x) >= 2H(x-1) + H(x/2)（这是最困难的部分）。我刚刚看到你答案的编辑，但那仍然是含糊其辞的。你不能这样用 1/n 替换 epsilon！你跳过了证明中最难的部分。如果你不同意，是否考虑在 math.stackexchange 上发帖以获得专家评论？ - Knoothe

你在那里基本上是在挥手示意。 - Knoothe

@SaeedAmiri：第一个错误是无关紧要的，因为您似乎只使用if来判断f(n) <= 2f(n-1) + f(n/2)，这很容易看出（例如，请参见我的答案）。显然，整个重点是找到一个上限（因为下限是平凡的）。很容易证明c^x的上限，其中c > 2（即本质上是(2+epsilon)^n）。难点在于提出一个本身就是O(2^x)的上限。这完全缺少了您的答案，并且您当前的方法不起作用（这就是HansLub所说的答案不足之处的含义）。 - Knoothe

Answer 2

使用记忆化，这两个函数都可以轻松地在O(n)时间内计算出来。但是该程序至少需要O(2^n)的时间，因此它是计算f(n)和g(n)的非常低效的方法。

为了证明该程序对于任何epsilon > 0最多需要O(2+epsilon)^n的时间：

设F(n)和G(n)分别为计算f(n)和g(n)所需的函数调用次数。显然（将加法计算作1次函数调用）：

F(0) = 1; F(n) = F(n-1) + G(n) + 1 G(1) = 1; G(n) = F(n-1) + G(n/2) + 1

然后可以证明：

• F和G是单调的
• F>G
• 定义H(1)=2；H(n)=2*H(n-1)+H(n/2)+1
• 显然，H>F
• 对于所有n，H(n)>2*H(n-1)
• 因此，对于足够大的n，H(n/2)/H(n-1)->0
• 因此，对于任意epsilon>0和足够大的n，H(n)<(2+epsilon)*H(n-1)
• 因此，H在O((2+epsilon)^n)中，其中epsilon>0
• (编辑：最初我得出结论上限是O(2^n)。这是不正确的，如nhahtdh指出，但请参见下文)
• 所以这是我能证明的最好的了...因为G<F<H，它们也在O((2+epsilon)^n)中，其中epsilon>0

---

附言（在看了Knoothes先生的解决方案之后）：因为我认为好的数学证明能够给予洞见，而不是大量的公式，而且SO存在于所有未来的人类（嗨，女孩们！）：

对于许多算法，计算f(n+1)需要两倍（三倍，...）f(n)的工作量，再加上一些额外的内容。如果这些额外的内容随着n的增加而相对减少（这通常是情况），使用像上面那样的固定epsilon并不是最优的。将上面的epsilon替换为n的某个递减函数ε(n)将在许多情况下（如果ε足够快地减少，例如ε(n)=1/n）产生一个上限O((2 + ε(n))^n ) = O(2^n)

- Hans Lub

---

2^n是下界，因此您应该说它是Omega(2^n)。 - nhahtdh

证明的步骤看起来太含糊了，让我不寒而栗... - nhahtdh

但这不是如何证明的方法。哪一步失败了，为什么？ - Hans Lub

更好的证明是通过反例：对于任意的 epsilon > 0，(2^n) * log(n) 属于 O((2 + epsilon)^n)，但不属于 O(2^n)。因此我的证明是错误的。 - Hans Lub

因此，对于足够大的n，有H（n/2）/H（n-1）-> 0 因此，对于所有ε> 0和足够大的n，有H（n）<(2 + ε)*H（n-1）。仅仅说某些事情是显而易见的并不能证明它，这是证明中错误的方法，就像说你找不到任何奇次度顶点具有欧拉通路的图表明每个具有欧拉通路的图的每个顶点都具有偶数度数一样，这是显然的但不是证明。 - Saeed Amiri

Answer 3

令f(0)=0，g(0)=0。

从函数中我们得到：

f(x) = f(x - 1) + g(x) 
g(x) = f(x - 1) + g(x/2)

将g(x)代入f(x)中，我们得到：

f(x) = f(x-1) + f(x -1) + g(x/2)

∴f(x) = 2f(x-1) + g(x/2)

展开这个式子，我们得到：

f(x) = 2f(x-1)+f(x/2-1)+f(x/4-1)+ ... + f(1)

假设s(x)是以下定义的函数：

s(x) = 2s(x-1)

现在很明显 f(x)=Ω(s(x))。

s(x) 的复杂度是 O(2^x)。

因此函数 f(x)=Ω(2^x)。

- Deepu

---

下限非常明确，更有趣的是上限。 - nhahtdh

-1：因为没有证明任何非平凡的东西，而且后面的陈述是不正确的。 - Knoothe

@Deepu：感谢倾听，但（不是要无礼），我真的不认为这个答案值得得到它所获得的赞数。你所展示的只是f(x) = Omega(2^x)，这很容易证明。难点在于证明f(x) = O(2^x)。（nhahtdh也发表了同样的评论）。所以，我仍然会给你的回答点个踩。对此我很抱歉。顺便说一句，只有s(x) = 2s(x-1)就足够了，不是吗？为什么要加上c呢？ - Knoothe

Answer 4

我认为很清楚地可以看出 f(n) > 2ⁿ，因为 f(n) > h(n) = 2h(n-1) = 2ⁿ。

现在我声称对于每个 n，都存在一个ε，使得：f(n) < (2+ε)ⁿ，为了证明这一点，让我们归纳一下，但是为了更容易理解，首先我将使用 ε = 1，以展示 f(n) <= 3ⁿ，然后再扩展它。

我们将使用强归纳法，假设对于每个 m < n，f(m) < 3^m，那么我们有：

f(n) = 2[f(n-1) + f(n/2 -1) + f(n/4 -1)+ ... +f(1-1)]

但是对于这部分：

A = f(n/2 -1) + f(n/4 -1)+ ... +f(1-1)

我们有：

f(n/2) = 2[f(n/2 -1) + f(n/4 -1)+ ... +f(1-1]) ==>

A <= f(n/2)   [1]

因此，我们可以重写 f(n)：

f(n) = 2f(n-1) + A < 2f(n-1) +f(n/2),

现在让我们回到我们的主张：

f(n) < 2*3^(n-1) + 2*3^(n/2)==>
f(n) < 2*3^(n-1) + 3^(n-1) ==>
f(n) < 3^n.  [2]

通过[2]，证明了f(n)∈O(3ⁿ)。

但是如果你想将其扩展到(2+ε)ⁿ的格式，只需使用1替换不等式，然后我们将有

对于 ε > 1/(2+ε)^n/2-1 → f(n) < (2+ε)ⁿ。[3]

此外，根据[3]，你可以说对于每个n都存在一个ε，使得f(n) < (2+ε)ⁿ，实际上存在常数ε，使得对于n > n₀，f(n)∈O((2+ε)ⁿ)。[4]

现在我们可以像 @Knoothe 一样使用 wolfarmalpha，通过设置 ε=1/n，然后我们将得到：

f(n) < (2+1/n)ⁿ，这导致 f(n) < e*2ⁿ，通过我们在开始时的简单下界，我们有：f(n)∈ Θ(2^n)。[5]

P.S：我没有精确计算 epsilon，但您可以简单地用笔和纸来计算，我认为这个 epsilon 不正确，但很容易发现它，如果难以找到，请告诉我是难题，我将写出答案。

- Saeed Amiri

---

是的，你最后的结论不仅适用于“一些”ε，而且适用于每个ε>0。 - Hans Lub

@HansLub，在 O 符号中，当我们说对于每个 n > n0 时，意味着 n0 是固定的常数。如果你看一下 epsilon 和 n0 之间的关系，epsilon 是依赖于 n0 的，因此我不能说对于每个 epsilon，因为 n0 是固定的，所以我应该关注于 n0 而不是 epsilon。与其说存在任何一个 epsilon，我应该说对于每个固定的 n0 存在 epsilon，使得...，而且最重要的是，我们应该找到 n0 对应的 epsilon 值。 - Saeed Amiri

当你说f是O(g)时，你不需要提到n0；你已经陈述了存在c和n0使得对于n > n0，f(n) < c*g(n)。而且，正如你所说的，不仅对于任意n0都存在一个epsilon，而且对于任意epsilon也存在一个n0，使得...因此对于任意epsilon，f是O((2+epsilon)^n)。 - Hans Lub

@HansLub，实际上我不同意“对于所有的epsilon都存在n0使得...”，因为当epsilon无限小时，n0将会是无限大，那么n0就不是一个固定的常数。 - Saeed Amiri

@HansLub：我现在可以自信地说，这里的答案有问题。f(x) = w(2^x)是不正确的。事实上，f(x) = Theta(2^x)！请看我的带有证明的答案。（当然，错误可能在我的证明中，但我没有任何地方含糊其辞，每一步都很容易验证） - Knoothe

@HansLub，现在看看我的答案，告诉我使用wolfarmalpha证明极限是聪明的部分还是证明的其他部分？ - Saeed Amiri