我在学校的作业中遇到了困难。我有一块巧克力棒,由黑色、白色或黑白相间的正方形组成。我需要将它分为两组,一组只有白色或黑白相间的块,另一组只有黑色或黑白相间的块。将巧克力棒分开意味着沿着分离单个正方形的线条水平或垂直地将其破裂。
给定巧克力棒的布局,我需要找到一种最佳分割方式,将暗色和白色立方体分开,并得到可能的最小碎片数,巧克力棒不大于50x50个正方形。
巧克力棒在标准输入上定义如下:第一行由两个整数M(巧克力棒中的行数)和N(列数)组成,然后有M列,每列包含N个字符,表示各个正方形(0-黑色,1-白色,2-混合)。
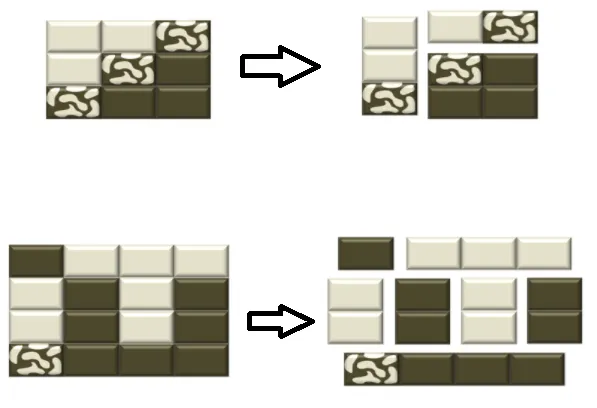
以下是一些最佳分割的示例,它们的输入分别是(正确输出为3和7):
我的问题是,我已经找到了一种解决方案,但我使用的算法不够快,如果巧克力条很大,比如这个例子:
然后我的程序需要10秒钟才能解决它(正确的解决方案为126,我应该能在2秒内解决它!)
我的算法大致如此,经过一些小的优化:迭代所有可能的切割线,然后对于新出现的2个矩形递归执行相同的操作,如果它们不能再分割,则返回1。
在迭代完所有可能的切割后,函数总是返回最小值,一旦找到最小值,就将其存储起来,如果我需要再次解决这个矩形,则只需返回该值。
我想也许如果我已经解决了一个特定的矩形,现在我需要解决一个行或列更大或更小的矩形,那么我可以以某种方式使用我已经拥有的解决方案,并将其用于新的问题。但我真的不知道如何实现这样的功能。目前,我的算法将其视为全新未解决的矩形。
到目前为止,我的代码如下:
给定巧克力棒的布局,我需要找到一种最佳分割方式,将暗色和白色立方体分开,并得到可能的最小碎片数,巧克力棒不大于50x50个正方形。
巧克力棒在标准输入上定义如下:第一行由两个整数M(巧克力棒中的行数)和N(列数)组成,然后有M列,每列包含N个字符,表示各个正方形(0-黑色,1-白色,2-混合)。
以下是一些最佳分割的示例,它们的输入分别是(正确输出为3和7):
3 3
1 1 2
1 2 0
2 0 0
4 4
0 1 1 1
1 0 1 0
1 0 1 0
2 0 0 0
我的问题是,我已经找到了一种解决方案,但我使用的算法不够快,如果巧克力条很大,比如这个例子:
40 40
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 1 2 1 1 0 0 0 0 0 0 0 0 0 0
0 0 0 1 1 1 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2 1 1 1 0 0 0 0 0 0 0 0 0 0
0 0 0 1 1 1 0 2 1 2 1 2 0 0 1 2 2 0 0 0 0 0 0 0 0 1 1 2 1 2 0 0 0 0 0 0 0 0 0 0
0 0 0 1 2 2 0 1 1 1 1 1 0 0 1 2 2 0 0 0 0 0 1 0 0 2 2 1 1 0 0 0 0 0 0 0 0 0 0 0
0 0 0 2 2 1 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1
0 0 0 0 0 0 0 1 1 2 2 0 0 0 1 2 2 1 2 1 0 0 0 0 0 1 2 1 2 0 0 1 0 0 0 0 0 0 0 0
0 0 0 0 0 0 1 2 2 1 2 0 0 0 0 0 2 1 2 2 0 0 0 0 0 2 1 2 1 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 2 2 2 1 1 0 0 0 0 0 2 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 2 1 0 0 0 0 0 0
0 2 1 2 1 0 2 2 2 2 1 2 2 0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 1 2 0 2 2 1 0 0 0 0 0 0
0 2 2 1 2 0 1 2 2 1 1 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 1 1 1 0 0 0 0 0 0
0 2 2 1 2 0 0 0 0 2 1 2 1 2 1 1 2 0 2 0 0 0 0 0 0 0 1 2 2 2 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 2 2 2 2 1 2 2 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0
0 0 0 0 0 0 0 0 0 1 2 1 1 2 2 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 2 2 0 0 0 0
0 0 0 0 0 0 0 2 1 2 0 0 2 2 1 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 1 1 0 0 0 0
0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2 2 2 0 0 0 0
0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 1 2 2 1 0 0 0 0 2 0 1 1 1 2 1 2 0 0 0 0 0
0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 2 0 0 0 0 0 0 2 1 2 2 2 1 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 2 0 0 0 0 0 0 1 2 1 1 2 2 0 0 0 0 0
0 0 0 0 0 0 1 2 1 2 2 1 0 0 0 0 0 0 0 1 2 1 2 0 0 0 0 0 0 0 0 0 2 1 2 0 0 0 0 0
0 0 0 0 0 0 1 2 2 1 1 1 1 0 0 0 0 0 0 0 0 1 1 1 2 0 0 0 0 0 0 0 0 0 0 2 1 1 0 0
0 0 0 0 0 0 1 1 1 1 1 2 2 0 0 0 0 0 0 0 0 1 1 1 2 0 0 0 0 0 0 0 0 0 0 1 2 1 0 0
0 0 0 0 0 0 1 2 2 2 1 1 1 0 0 0 0 0 0 0 0 1 2 1 2 0 0 0 0 0 0 0 0 0 0 2 2 2 1 0
0 0 0 0 0 0 0 0 0 1 2 1 2 0 0 0 0 0 0 0 0 1 1 1 2 2 0 0 0 0 0 0 0 0 0 1 2 1 1 0
0 0 0 2 1 1 2 2 0 1 2 1 1 0 0 0 0 0 2 2 1 2 2 1 2 2 0 0 0 0 0 0 0 0 0 1 2 2 2 0
0 0 0 2 2 2 1 1 0 0 1 2 2 2 0 0 0 0 2 2 2 1 1 2 1 1 2 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 2 1 2 2 1 1 0 2 1 2 1 2 1 2 1 1 2 1 1 1 1 1 2 2 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 2 2 2 2 1 0 1 1 1 1 1 1 2 1 1 2 2 1 0 1 2 1 2 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 1 1 1 0 0 2 1 1 1 2 1 2 0 0 1 2 1 2 1 2 2 0 0 0 0 0 0 0 1 1 1 0 0 0
0 0 0 0 0 0 0 0 0 0 0 1 2 2 1 1 2 2 1 1 1 1 1 1 1 2 1 0 0 0 0 0 0 0 2 2 2 0 0 0
0 0 0 0 0 0 0 1 1 1 2 0 0 1 1 1 2 2 1 2 2 2 1 0 0 0 1 1 1 0 0 0 0 0 1 2 1 0 0 0
0 0 0 0 0 0 0 2 1 1 2 0 0 0 0 0 0 2 2 2 1 1 1 0 0 0 1 2 2 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 2 2 2 2 0 0 0 0 0 0 2 1 1 1 2 0 0 0 0 1 2 2 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 2 2 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 1 1 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2 1 0 0 0 0 0 0 0 1 1 2 0 2
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 2 2 0 0 0 0 0 0 0 1 2 1 0 0
0 0 0 0 0 0 0 0 0 2 2 2 0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 2 0 0 0 0 0 0 0 1 2 1 0 0
0 0 0 0 0 0 0 0 0 2 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 1 1 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
然后我的程序需要10秒钟才能解决它(正确的解决方案为126,我应该能在2秒内解决它!)
我的算法大致如此,经过一些小的优化:迭代所有可能的切割线,然后对于新出现的2个矩形递归执行相同的操作,如果它们不能再分割,则返回1。
在迭代完所有可能的切割后,函数总是返回最小值,一旦找到最小值,就将其存储起来,如果我需要再次解决这个矩形,则只需返回该值。
我想也许如果我已经解决了一个特定的矩形,现在我需要解决一个行或列更大或更小的矩形,那么我可以以某种方式使用我已经拥有的解决方案,并将其用于新的问题。但我真的不知道如何实现这样的功能。目前,我的算法将其视为全新未解决的矩形。
到目前为止,我的代码如下:
#include <stdio.h>
#include <stdlib.h>
unsigned int M, N;
unsigned int ****pieces; ////already solved rectangles, the value of pieces[y0][x0][y1][x1] is the optimal number of pieces in which the particular rectangle(that has upperleft corner in [x0,y0] and bottomright corner in[x1,y1]) can be divided
int ****checked;
unsigned int inf;
unsigned int minbreaks(int mat[M][N], unsigned int starti, unsigned int startj, unsigned int maxi, unsigned int maxj) {
if (pieces[starti][startj][maxi][maxj] != 0) {
return pieces[starti][startj][maxi][maxj];
} else {
unsigned int vbreaks[maxj - 1];
unsigned int hbreaks[maxi - 1];
for (unsigned int i = 0; i < maxj - 1; i++) {
vbreaks[i] = inf;
}
for (unsigned int i = 0; i < maxi - 1; i++) {
hbreaks[i] = inf;
}
unsigned int currentmin = inf;
for (unsigned int i = starti; i < maxi; i++) {
for (unsigned int j = startj; j < maxj - 1; j++) {
if (mat[i][j] != 2) {
for (unsigned int k = startj + 1; k < maxj; k++) {
if (vbreaks[k - 1] == inf) {
for (unsigned int z = starti; z < maxi; z++) {
if (!checked[i][j][z][k]) {
if (mat[z][k] != 2 && mat[i][j] != mat[z][k]) {
vbreaks[k - 1] = minbreaks(mat, starti, startj, maxi, k) + minbreaks(mat, starti, k, maxi, maxj);
if (vbreaks[k - 1] < currentmin) {
currentmin = vbreaks[k - 1];
}
break;
}
checked[i][j][z][k] = 1;
}
}
}
}
}
}
}
for (unsigned int i = starti; i < maxi - 1; i++) {
for (unsigned int j = startj; j < maxj; j++) {
if (mat[i][j] != 2) {
for (unsigned int k = starti + 1; k < maxi; k++) {
if (hbreaks[k - 1] == inf) {
for (unsigned int z = startj; z < maxj; z++) {
if (!checked[i][j][k][z]) {
if (mat[k][z] != 2 && mat[i][j] != mat[k][z]) {
hbreaks[k - 1] = minbreaks(mat, starti, startj, k, maxj) + minbreaks(mat, k, startj, maxi, maxj);
if (hbreaks[k - 1] < currentmin) {
currentmin = hbreaks[k - 1];
}
break;
}
checked[i][j][k][z] = 1;
}
}
}
}
}
}
}
if (currentmin == inf) {
currentmin = 1;
}
pieces[starti][startj][maxi][maxj] = currentmin;
return currentmin;
}
}
int main(void) {
FILE *file = stdin;
fscanf(file, "%u %u", &M, &N);
int mat[M][N];
pieces = malloc(sizeof (unsigned int***)*M);
checked = malloc(sizeof (int***)*M);
for (unsigned int i = 0; i < M; i++) {//initialize the pieces,checked and mat arrays.
pieces[i] = malloc(sizeof (unsigned int**)*N);
checked[i] = malloc(sizeof (int**)*N);
for (unsigned int j = 0; j < N; j++) {
int x;
fscanf(file, "%d", &x);
mat[i][j] = x;
pieces[i][j] = malloc(sizeof (unsigned int*)*(M + 1));
checked[i][j] = malloc(sizeof (int*)*M);
for (unsigned int y = i; y < M + 1; y++) {
pieces[i][j][y] = malloc(sizeof (unsigned int)*(N + 1));
for (unsigned int x = j; x < N + 1; x++) {
pieces[i][j][y][x] = 0;
}
}
for (unsigned int y = 0; y < M; y++) {
checked[i][j][y] = malloc(sizeof (int)*N);
for (unsigned int x = 0; x < N; x++) {
checked[i][j][y][x] = 0;
}
}
}
}
inf = M * N + 1; //number one bigger than maximal theoretically possible number of divisions
unsigned int result = minbreaks(mat, 0, 0, M, N);
printf("%u\n", result);
return (EXIT_SUCCESS);
}
那么,有人有改进的想法吗?
n×m条分成m-1种方式,也可以垂直地将其分成n-1种方式。这样就有n-1+m-1种方法来分割条形图。对于每个分割,你需要解决两个较小的问题。完成。 - n. m.solve(bar): if bar is uniform return 1; else return minimum_of (each way to make (bar = bar1 + bar2): solve(bar1) + solve(bar2))。你是如何在其中嵌套四个循环的? - n. m.