3个回答
1
使用平衡化的标准化四叉树。
标准化:收集所有x坐标,对它们进行排序并用排序后的数组中的索引替换它们。y坐标同理。
平衡化:在构建四叉树时,总是在中间坐标处分割。
因此,当您获得一个矩形时,您需要使用一些矩形id在树中标记正确的节点。如果在下面找到任何其他重叠的矩形,则将它们收集到集合中。完成后,如果向量不为空(找到重叠的矩形),则创建一个新矩形来表示子矩形的并集。如果计算的矩形比刚插入的矩形大,则使用新计算的矩形再次应用算法。重复此过程,直到它不再增长,然后移动到下一个输入矩形。
为了提高性能,四叉树中的每个节点都存储所有重叠该节点的矩形,并将其标记为结束节点。
复杂度:初始归一化为O(NlogN)。插入和检查重叠将是O(log(N)^2)。您需要为原始的N个矩形以及重叠执行此操作。每次找到重叠时,您都会消除至少一个原始矩形,因此最多可以找到(N-1)个重叠。因此,总体而言,您需要进行2N次操作。因此,总体复杂度将是O(N(log(N)^2))。
这比其他方法更好,因为您不需要检查任何两个矩形是否重叠。
- Sorin
6
2我不明白如何仅通过检查重叠可以达到O(Log²(N))。 - user1196549
检查给定矩形下的节点将为您提供与该矩形重叠的所有内容。这具有复杂度
O(Log(N) ^2)。由于每个节点都保留与其任何部分重叠的所有矩形,因此一旦您拥有完全被矩形覆盖的节点,就不需要再往下挖掘。这些节点最多有O(Log(N) ^2)个。在纸上举个例子来说服自己。 - Sorin嗯,如果所有的矩形都重叠,那么枚举重叠部分只需要O(N)的时间复杂度... - user1196549
这是正确的,但你只需要做一次,因此在总体复杂度中进行了摊销。你之所以只做一次,是因为你折叠它们,所以下一次你只会得到一个折叠后的矩形。 - Sorin
你在解决方案中使用了 https://en.wikipedia.org/wiki/Quadtree 或 https://en.wikipedia.org/wiki/K-d_tree 吗? - DAle
我建议使用QuadTree,因为它更容易理解。我认为K-d树在相同的约束条件下也可以工作。 - Sorin
1
我认为R-Tree可以在这里发挥作用。R-Tree索引矩形区域,并允许您在低维度的“普通”查询中以O(log n)的时间进行插入、删除和查询(例如,相交查询)。
思路是逐个处理矩形,对于每个矩形,执行以下操作:
1. 在当前R-Tree上执行相交查询(开始为空) 2. 如果有结果,则从R-Tree中删除结果,将当前矩形与所有结果矩形合并,并插入新合并的矩形(对于最后一步跳转到步骤1) 3. 如果没有结果,只需将矩形插入R-Tree中
总共会执行:
1. 步骤1中的O(n)相交查询(O(n log n)) 2. 步骤3中的O(n)插入步骤(O(n log n)) 3. 步骤2中最多n次删除和n次插入步骤。这是因为每次执行步骤2时,您都会将矩形数目至少减少1个(O(n log n))
理论上,您应该可以使用 O(n log n) 的时间复杂度完成,但是最后合并步骤(对于大矩形)可能具有较低的选择性,并且可能需要超过 O(log n) 的时间,但根据数据分布情况,这不应该破坏总体运行时间。
思路是逐个处理矩形,对于每个矩形,执行以下操作:
1. 在当前R-Tree上执行相交查询(开始为空) 2. 如果有结果,则从R-Tree中删除结果,将当前矩形与所有结果矩形合并,并插入新合并的矩形(对于最后一步跳转到步骤1) 3. 如果没有结果,只需将矩形插入R-Tree中
总共会执行:
1. 步骤1中的O(n)相交查询(O(n log n)) 2. 步骤3中的O(n)插入步骤(O(n log n)) 3. 步骤2中最多n次删除和n次插入步骤。这是因为每次执行步骤2时,您都会将矩形数目至少减少1个(O(n log n))
理论上,您应该可以使用 O(n log n) 的时间复杂度完成,但是最后合并步骤(对于大矩形)可能具有较低的选择性,并且可能需要超过 O(log n) 的时间,但根据数据分布情况,这不应该破坏总体运行时间。
- SaiBot
0
这个问题可以通过平面扫描和空间数据结构的组合来解决:我们沿着扫描线合并相交的矩形,并将任何在扫描线后面的矩形放入空间数据结构中。每次我们得到一个新合并的矩形时,我们检查空间数据结构是否存在与此新矩形相交的任何矩形,并在找到时进行合并。
如果扫描线后面的任何矩形(R)与扫描线下方的某个矩形(S)相交,则 R 最靠近扫描线的两个角之一位于 S 内。这意味着空间数据结构应该存储点(每个矩形两个点),并回答关于任何点是否位于给定矩形内的查询。实现这种数据结构的一种明显方法是使用线段树,其中每个叶子包含具有相应 y 坐标处顶部和底部边的矩形,每个其他节点指向其包含最右侧矩形(其右侧最靠近扫描线)的后代之一。
要使用这样的线段树,我们应该压缩(归一化)矩形角的 y 坐标。
如果扫描线后面的任何矩形(R)与扫描线下方的某个矩形(S)相交,则 R 最靠近扫描线的两个角之一位于 S 内。这意味着空间数据结构应该存储点(每个矩形两个点),并回答关于任何点是否位于给定矩形内的查询。实现这种数据结构的一种明显方法是使用线段树,其中每个叶子包含具有相应 y 坐标处顶部和底部边的矩形,每个其他节点指向其包含最右侧矩形(其右侧最靠近扫描线)的后代之一。
要使用这样的线段树,我们应该压缩(归一化)矩形角的 y 坐标。
- 压缩 y 坐标
- 按矩形左侧 x 坐标排序。
- 将扫描线移动到下一个矩形,如果它经过一些矩形的右侧,则将它们移动到线段树中。
- 检查当前矩形是否与扫描线上的任何东西相交。如果没有,请转到步骤 3。
- 检查在第 4 步找到的矩形的并集是否与线段树中的任何东西相交,并递归合并,然后转到步骤 4。
- 当步骤 3 到达列表末尾时,获取扫描线下方的所有矩形和线段树中的所有矩形,并解压缩它们的坐标。
最坏情况时间复杂度由线段树确定:O(n log n)。空间复杂度为 O(n)。
- Evgeny Kluev
2
这已经是几年前的事了,但你有这张图片或这种方法的来源吗?我想知道为什么在y轴上进行归一化是必要的,以及如何高效地执行第4步。 - nicholas
网页内容由stack overflow 提供, 点击上面的可以查看英文原文,
原文链接
原文链接
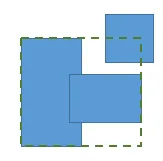
可以合并不是必须合并。) - greybeard