虽然这是一个四年前的帖子，但我在谷歌搜索我的问题时偶然发现了它。
我在当前的简历应用程序中遇到了类似的问题。我想出了一个简单而有些笨拙的解决方案来找到最大值。虽然不完全相同，因为我最大化矩形的面积而没有固定比例的边。
我还不知道我的解决方案是否找到了最优解，或者它是否在所有情况下都有效。我认为应该有一种更有效的方法，所以我期待着您的意见。
首先，假设我们有一组形成我们（凸）四边形的4个点：
x y
P1 -2 -5
P2 1 7
P3 4 5
P4 3 -2
对于这个过程，最左边的点是P1，接下来的点按顺时针方向编号。它看起来像这样：
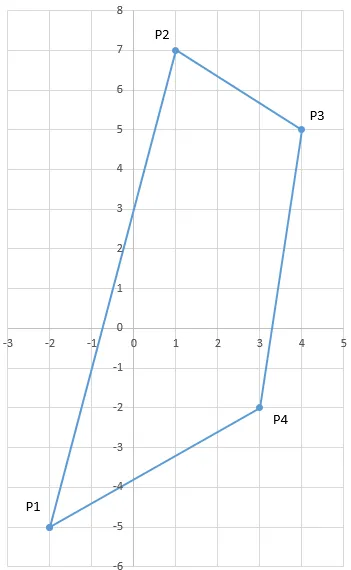
我们接着创建点之间的线性函数。对于每个函数，我们需要知道斜率k和距离0的距离d。
k就是两个点在Y轴上的差除以X轴上的差。
d可以通过解线性函数得出。因此我们有：
k=dy/dx
d=y1-k*x1
我们还需要反函数。
k_inv = 1/k
d_inv = -d/k
我们随后为四边形的每一侧创建函数和反函数。
k d k d
p1p2 4 3 p1p2_inv 0.25 -0.75
p2p3 -0.67 7.67 p2p3_inv -1.5 11.5
p3p4 7 -23 p3p4_inv 0.14 3.29
p4p1 0.6 -3.8 p4p1_inv 1.67 6.33
如果我们有完全水平或垂直的线条，我们将在一个函数或反函数中得到DIV/0，因此我们需要单独处理这种情况。
现在，我们遍历所有由两个斜率带有不同符号的函数所包围的角落。在我们的情况下，这将是P2和P3。
我们从P2开始，迭代通过适当的步长在P2和P1、P3中较高的一个之间的y值，并使用反函数计算函数之间水平方向上的距离。这将给我们矩形的一侧。
a=p2p3_inv(y)-p1p2_inv(y)
在两个x值 x = p2p3_inv(y) 和 x = p1p2_inv(y)处，我们计算y与两个相反函数的差，并将其与当前y位置的距离作为我们矩形的第二条边的候选值。
b_candidate_1 = y-p4p1(p2p3_inv(y))
b_candidate_2 = y-p4p1(p1p2_inv(y))
b_candidate_3 = y-P3p4(p2p3_inv(y))
b_candidate_4 = y-P3p4(p1p2_inv(y))
较小的四个参数将成为边b的解决方案。面积显然变为a*b。
我在Excel中进行了一个快速示例以演示：
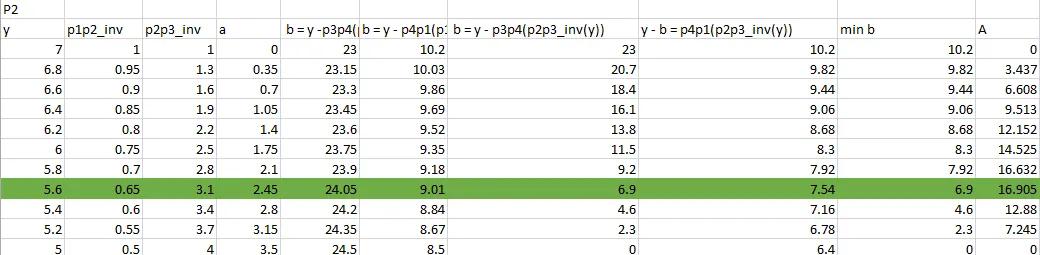
最小的b值为6.9，因此解的右上角在p2p3处，矩形向左和向下分别水平扩展a和垂直扩展b。
因此，矩形的四个点分别是：
Rect x y
R1 0.65 -1.3
R2 0.65 5.6
R3 3.1 5.6
R4 3.1 -1.3
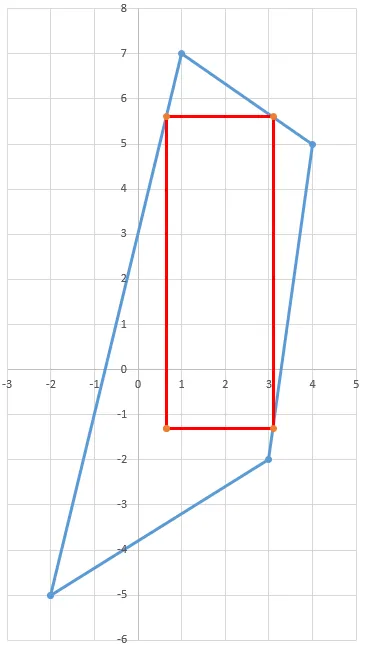
我将把这个内容转化为C++代码，并运行一些测试，以确定解决方案是否具有普适性，或者这只是“运气”。
我认为也可以用函数替换A=a*b中的a和b，并将其放入一个线性公式中，在满足p1p2仅在P1和P2之间定义的条件下进行最大化...
以下是我试图实现的内刻最大化的两个示例：
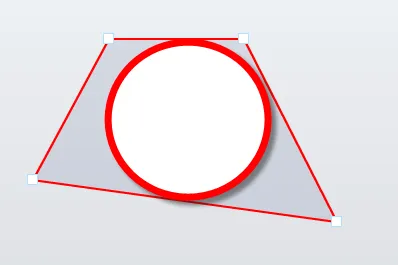
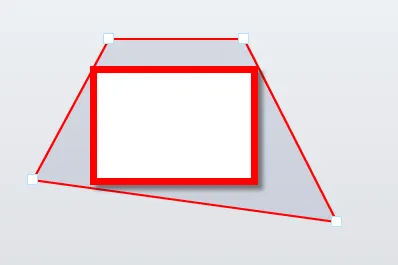我已经进行了一些初步搜索，但没有找到确定的答案。似乎某种形式的动态规划可能是解决方案。这应该是一个线性优化问题，比我发现的更常见，也许我正在寻找错误的术语。