为什么斐波那契数列的时间复杂度是O(2^n)而不是O(logn)?

Question

我之前修过离散数学（其中学习了主定理、大Omega/Theta/O等），但似乎已经忘记了O(logn)和O(2^n)之间的区别（不是在大O理论意义下的区别）。通常情况下，我知道像归并排序和快速排序这样的算法是O(nlogn)，因为它们将初始输入数组重复分成子数组，直到每个子数组的大小都是1，然后在递归回到树的顶层之前进行排序。这样得到的递归树高度为logn+1。但是如果使用n/b^x = 1（如在此答案中所述），计算递归树的高度，则似乎总是得到树的高度为log(n)。

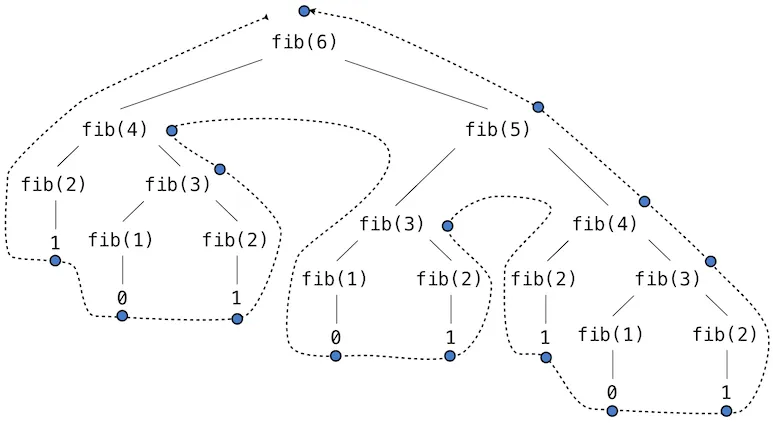
如果使用递归来解决斐波那契数列，我认为您也会得到一棵大小为logn的树，但由于某种原因，该算法的时间复杂度却是O(2^n)。我认为可能的差异是因为您必须记住每个子问题的所有斐波那契数字才能获得实际的斐波那契数字，这意味着必须重新调用每个节点的值，但是似乎在归并排序中，也必须使用（或至少排序）每个节点的值。然而，这与二分搜索不同，因为基于树的每个层次的比较仅访问某些节点，所以我认为这就是混淆的原因。

因此，具体来说，是什么导致斐波那契数列具有与归并/快速排序等算法不同的时间复杂度？

- loremIpsum1771

---

http://stackoverflow.com/questions/12388791/analysis-of-fibonacci-algorithm - Michael Xu

Answer 1

其他答案都是正确的，但没有很清楚地解释 - 斐波那契算法和分治算法之间的巨大差异从何而来？事实上，两类函数的递归树形状相同 - 都是二叉树。

理解的关键其实非常简单：将递归树的大小视为输入大小n的函数。

在斐波那契递归中，输入大小n是树的高度；对于排序，输入大小n是树的宽度。在前一种情况下，树的大小（即复杂度）是输入大小的指数，在后一种情况下，它是输入大小乘以树的高度，通常只是输入大小的对数。

更正式地说，首先从这些有关 二叉树的事实开始：

• 在二叉树中，叶子节点的数量 n 等于非叶子节点的数量加一。因此，二叉树的大小为 2n-1。
• 在一个 完美 的二叉树中，所有非叶子节点都有两个子节点。
• 对于一个有 n 个叶子节点的完美二叉树，其高度 h 等于 log(n)；对于一个随机的二叉树，h = O(log(n))；对于一个退化的二叉树，h = n-1。

直观地说：

• 对于使用递归算法排序一个长度为n的数组，递归树有n个叶子节点。因此，树的宽度为n，树的高度平均为O(log(n))，在最坏情况下为O(n)。

• 对于使用递归算法计算斐波那契数列中的第k个元素，递归树有k个层级（要想知道原因，请考虑到 fib(k) 调用了 fib(k-1)，后者调用了 fib(k-2)，以此类推）。因此，树的高度为k。为了估计递归树的宽度和节点数量的下界，需要考虑到由于 fib(k) 还会调用 fib(k-2)，因此递归树中有一个高度为 k/2 的完美二叉树。如果提取出来，该完美子树将具有 2^k/2 个叶子节点。因此，递归树的宽度至少为 O(2^{k/2}) 或等价于2^O(k)。

关键区别在于：

- 对于分治算法，输入大小是二叉树的宽度。 - 对于斐波那契算法，输入大小是二叉树的高度。

因此，在第一种情况下，树中节点的数量为O(n)，但在第二种情况下，树的大小为2^O(n)。与输入大小相比，斐波那契树要大得多。

您提到主定理；然而，该定理无法用于分析斐波那契的复杂性，因为它仅适用于在每个递归级别上实际“划分”输入的算法。斐波那契不会“划分”输入；实际上，在第i级别的函数为下一级别i+1几乎产生了两倍的输入。

- kfx

---

因为斐波那契数列在每次递归调用时只是简单地递减，所以它的树高度是线性的，而不像归并排序那样对输入大小进行重复折半，其树高度是对数级别的。而树的宽度具体为2^k，因为在返回语句中有两个递归调用，并且存在重复的子问题需要解决。 - loremIpsum1771

是的，有 k 个级别（因为对于每个 i，fib(i) 求值 fib(i-1)），并且有 O(2^k) 个叶节点，因为树的第 i+1 级大约有比第 i 级多两倍的节点。 - kfx

绘制递归树是了解 i+1 层节点数是前一层两倍的唯一方法吗？我只是想获得宽度的直觉。 - loremIpsum1771

不是的，但是绘图可以使事情变得更容易。需要注意的重要事项是，对于除了非常小的值（<=2）之外的所有值，每次调用 fib 都会生成两个以上的 fib 调用。因此，下一级具有两倍的 fib 调用量。当然，对于归并排序、快速排序等许多不同函数来说，递归树的形状基本相同（二叉树）。 - kfx

我不明白你为什么认为这个操作会有很大的差别。实际上，合并已排序数字列表比加两个数字要复杂得多，不是吗？关注树的大小-这是必要和充分的差异。我将用更严谨的数学扩展答案。 - kfx

Answer 2

为了回答这个问题的核心，即“为什么是斐波那契而不是归并排序”，您应该关注这个关键区别：

• 从归并排序得到的树每个级别都有N个元素，有log(n)个级别。
• 由于F(N)公式中F(n-1)的存在，所以从斐波那契得到的树有N个级别，每个级别的元素数量可以差别很大：它可以非常低（靠近根或靠近最低的叶子），也可以非常高。当然，这是因为重复计算相同的值。

要看到我所说的“重复计算”是什么意思，请看一下计算F(6)的树：

^{_{来自斐波那契树图片：http://composingprograms.com/pages/28-efficiency.html}}

你看到F(3)被计算了多少次？

- William

---

似乎其他答案都在暗示，归并排序等算法通过每次递归调用将输入大小按因子减小到基本条件，而斐波那契和汉诺塔等算法仅通过加法/减法每次减小大小，需要更长时间才能达到基本情况。但你是说重复计算（可以通过DP / Memoization解决）是导致差异的原因？还是两者都有？ - loremIpsum1771

问题在于同样的问题被重复了。这是一个求前N个数之和的递归实现：S(N) = N + S(N-1)，其中基本情况为S(0) = 0。通过加法/减法进行缩减，但这是O(N)的。 - William

请注意，当然，如果您添加记忆化，则斐波那契数列的时间复杂度将变为O(n)。 - William

Answer 3

据我理解，你推理错误的地方在于使用递归实现来计算斐波那契数列中的f(n)，输入大小会被减少一半（或其他某个因子），但事实并非如此。每次调用（除了“基本情况”0和1）都会使用恰好2个递归调用，因为没有可能重复使用先前计算出的值。根据Wikipedia上主定理的介绍，递归式为：

f(n) = f (n-1) + f(n-2)

这是一个无法应用主定理的情况。

- Codor

Answer 4

使用递归算法，斐波那契数列（N）的运算次数约为2^N（加法）。因此它的时间复杂度为O(2^N)。

使用缓存（记忆化）技术，运算次数约为N，因此它的时间复杂度为O(N)。

时间复杂度为O(N log N)的算法通常是遍历每个项目（O(N)），分裂递归和合并 ... 分裂成2个 => 您需要做log N次递归。

- guillaume girod-vitouchkina

---

递归算法是指数级的，而不是二次的。你从哪里得到n^2/2的？ - interjay

@interjay - 绝对是2的N次方 - guillaume girod-vitouchkina

更准确地说，大约是1.618^n。 - interjay

Answer 5

考虑下面的实现

int fib(int n)
{
    if(n < 2)
      return n;
    return fib(n-1) + fib(n-2)
}

我们用 T(n) 表示计算 fib(n) 所需的操作次数。由于 fib(n) 调用了 fib(n-1) 和 fib(n-2)，这意味着 T(n) 至少为 T(n-1) + T(n-2)。进而可以得出 T(n) > fib(n)。有一个直接的公式可以计算 fib(n)，它是一些常量的指数。因此，T(n) 至少是指数级别的。证毕。

- Armen Tsirunyan

Answer 6

归并排序的时间复杂度为O(n log(n))。快速排序最好情况下为O(n log(n))，最坏情况下为O(n^2)。

其他答案已经解释了为什么朴素递归斐波那契数列的时间复杂度是O(2^n)。

如果你听说过Fibonacci(n)可以达到O(log(n))，那是因为可以使用迭代和重复平方来计算，可以使用矩阵方法或者lucas序列方法。下面是使用lucas序列方法的示例代码（注意：每次循环时n被2整除）：

/* lucas sequence method */
int fib(int n) {
    int a, b, p, q, qq, aq;
    a = q = 1;
    b = p = 0;
    while(1) {
        if(n & 1) {
            aq = a*q;
            a = b*q + aq + a*p;
            b = b*p + aq;
        }
        n /= 2;
        if(n == 0)
            break;
        qq = q*q;
        q = 2*p*q + qq;
        p = p*p + qq;
    }
    return b;
}

- rcgldr

Answer 7

与使用主定理不同，可以应用主定理来解决问题。但是需要应用递减函数的主定理，而不是分治函数的主定理。如果没有定理，可以通过以下递归关系进行求解：

f(n) = f(n-1) + f(n-2)

f(n) = 2*f(n-1) + c 

假设 c 等于 1，因为它是常数且不影响复杂度。

f(n) = 2*f(n-1) + 1 

并将该函数替换 k 次

f(n) = 2*[2*f(n-2) +1 ] + 1   
f(n) = 2^2*f(n-2) + 2 + 1


f(n) = 2^2*[2*f(n-3) + 1] +2 + 1 
f(n) = 2^3*f(n-3) + 4 + 2 + 1
.
.
.
f(n) = 2^k*f(n-k) + 2^k-1 + 2^k-2 + ... + 4 + 2 + 1

现在假设 n=k

f(n) = 2^n*f(0) + 2^n-1 + 2^n-2 + ... + 4 + 2 + 1

f(n) = 2^n+1 thus complexity is O(2^n)

请查看此视频，了解递减函数的主定理。

- Tamer