如何高效计算列表中两点之间的最大距离？

Question

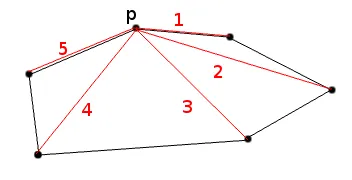
我有一组点的列表L，它们的坐标为(x, y)，使用欧几里得距离测量方式。

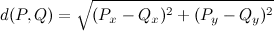
如何找到该列表中两个点之间的最大距离？或者更正式地说：如何找到

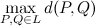
简单方法

解决这个问题最简单的方法似乎是尝试所有可能的情况：

def find_max_dist(L):
    max_dist = d(L[0], L[1])
    for i in range(0, len(L)-1):
        for j in range(i+1, len(L):
            max_dist = max(d(L[i], L[j]), max_dist)
    return max_dist

为了加快计算速度，在循环中可以使用平方距离，最后返回根值。

该方法的运行时间复杂度为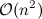，其中n是列表L的长度。(空间复杂度为常数)

凸包

显然，没有比O(n)更快的算法，因为必须至少查看列表中的每个元素一次。

最高距离将在凸包的元素之间。但是很容易证明，计算凸包的复杂度至少为O(nlogn)，而Graham扫描似乎可以做到这一点。但是，在找到复杂的外壳之后，我仍然需要获得最大距离。所以我的最终代码为：

def find_max_dist_graham_triv(L):
    H = Graham_scan(L)
    return find_max_dist(L)

现在，这是一个我不确定的点。我认为可以像这样改进：

def find_max_dist_graham_c1(L):
    H = Graham_scan(L)  # Get ordered list of convex hull points
    max_dist = d(L[0], L[1])
    for i in range(0, len(L)-1):
        loop_max_dist = 0
        for j in range(i+1, len(L):
            curr_dist = d(L[i], L[j])
            if curr_dist < loop_max_dist:
                break
            loop_max_dist = curr_dist
            max_dist = max(loop_max_dist, max_dist)

    return max_dist

这个想法是，当您选取凸包的一个点并从其相邻的点开始时，对角线会不断增加，达到最大值，然后不断减少。虽然我不确定这是否正确。

直观地说，我会继续改进算法：一旦第一内部循环完成，我们就找到了该循环的“最长对角线”。该对角线将所有其他凸壳点分为两个不相交的集合。每条更长的对角线都必须由这些集合中的点组成（对吗？）：

def find_max_dist_graham_c1(L):
    H = Graham_scan(L)  # Get ordered list of convex hull points
    max_dist = d(L[0], L[1])  # Get a fist idea what the longest distance might be

    i = 0
    p1 = L[i]  # Grab a random point
    loop_max_dist = 0
    for j in range(1, len(L):
        curr_dist = d(L[i], L[j])
        if curr_dist < loop_max_dist:
            break
        loop_max_dist = curr_dist
        max_dist = max(loop_max_dist, max_dist)
    # Every diagonal that is longer than the best one found with L[0]
    # has to have points in both of the following two sets (correct?):
    # [1...j] and [j+1...len(L)]

    # Try to find a neighboring diagonal that is longer.
    change = True
    while change:
        change = False
        if d(L[i-1], L[j+1]) > max_dist:
            max_dist = d(L[i-1], L[j+1])
            i -= 1
            j += 1
            change = True
        elif d(L[i+1], L[j-1]) > max_dist:
            max_dist = d(L[i+1], L[j-1])
            i += 1
            j -= 1
            change = True
    return max_dist

凸包上的每个点P都有一个凸包上的点Q，使得PQ是包括P的最长对角线。但是，P是否也是Q的最长对角线的“端点”呢？

我真的不确定这个算法是否正确。它的复杂度是O（n log n）。

我想问题已经被很好地分析了，所以能否有人为此留下一些注释呢？

虽然我有很多子问题，但主要问题是：

在点列表中查找两点之间最大距离的有效方法是什么？

- Martin Thoma

---

你想找到距离最远的两个点吗？ - CMPS

@Amir：不是。我想要得到两个最远点之间的距离。 - Martin Thoma

两个固定点之间的距离如何变化？ - CMPS

@Amir：两个固定点之间的距离是不会变化的。你为什么要问呢？ - Martin Thoma

@moose，user1990169 的意思是说，你可以在这里使用三分搜索（同样的工作也可以使用二分搜索完成）。 - Priyank Bhatnagar

Answer 1

您应该查阅旋转卡壳（Rotating calipers）(http://en.wikipedia.org/wiki/Rotating_calipers) - 它们被广泛用于解决这类问题。此外，您的假设是错误的。对于凸多边形上的固定点 p，对角线可以先增加，然后减少，再增加，最后又减少。至少我有一个案例是如此。

一种启发式方法是：选择一个点 x。从中找到最远的点 y。从y找到最远的点 z。 d(z,y) 是一个很好的估计。

说明对角线的图像：

1 -> 2：递增；2 -> 3: 递减；3 -> 4：递增；4 -> 5：递减。该图可能不精确，请将3和4指向的点稍微远离p（在同一条线上）。

- Amtrix

---

你有这个启发式的参考资料吗？我想要了解一下。 - Nimrod Morag

Answer 2

假设你有一个点的均匀分布，可以执行以下操作：

找到最大和最小的X坐标 - （O（n））。这些值应该帮助您选择当前点集的“最佳”常数k。不同的k值只会影响算法的复杂度。

考虑一种新的数据结构，类似于矩阵，是向量或链表的向量，让我们称之为“结构”，其中structure [i]是相应的向量/链接列表（如上所述）。按以下方式填充此数据结构：structure [i]应包含具有x坐标在[max_x + ik，max_x +（i + 1）k]范围内的点，这将花费另外O（n）时间和O（n）额外空间。现在，您可以按y坐标对structure [i]的每个条目进行排序。完成这些操作后，就足以计算以下点集之间的距离（暴力计算）：structure [0]，structure [structure.length（）-1]，每个其他structure [i]的极端（第一个和最后一个索引处的条目）。

基本上，这几乎与计算凸包并开始计算在凸包上的点的距离相同，不同之处在于选择正确的k可能使其更快或更慢。最坏情况下的复杂度为O（n ^ 2），最佳情况下的复杂度为O（nLg（n））。其中k将影响在排序更大的点组或具有更多点之间计算距离之间进行交易。

- Alexandru Barbarosie

---

假设您有一个点的均匀分布，您可以做以下操作 - 我没有那个。 - Martin Thoma