为什么这个二叉树遍历算法的时间复杂度为O(NlogN)？

Question

我现在正在学习《程序员面试金典》这本书，并在做一道二叉树的练习题。书中给出的代码片段复杂度为 O(NlogN)，但是我不明白为什么。如果算法复杂度是 O(N) 的话我能理解，但是我不知道他们的分析中哪里来的 logN。

int getHeight(TreeNode root) {
    if (root == null) return -1; // Base case
    return Math.max(getHeight(root.left), getHeight(root.right)) + 1;
}

boolean isBalanced(TreeNode root) {
    if (root == null) return true; // Base case

    int heightDiff = getHeight(root.left) - getHeight(root.right);
    if (Math.abs(heightDiff) > 1) {
        return false;
    } else { 
        // Recurse
        return isBalanced(root.left) && isBalanced(root.right);
    }
}

- Jessica

Answer 1

如果我们遇到一个不平衡的节点，我们会尽早返回false，这是最优情况。该算法处理的“最坏情况”是完全平衡的树，因为我们没有尽早返回false。为了举例说明，让我们使用一个有n个节点的完美二叉树。

第一次调用会触发每个节点的getHeight()，所以会访问~n个节点。根级别的总工作量为O(n)。

接下来的两个调用(root.left.isBalanced()和root.right.isBalanced())会在后续节点上触发getHeight()，但每个节点只会在~1/2 n个节点上调用它。每个高度的总工作量也是O(n)。

接下来的4个调用将在每个n/4个节点上调用getHeight。因此，2个高度的总工作量也是O(n)。

如果您看到模式，每个树级别的总工作量都是O(n)，因此所有级别的总工作量为O(n) * 完美树中的级别数，结果为O(nlogn)。

- Peter Cheng

Answer 2

getHeight的复杂度肯定是线性的，它只访问子树中的每个元素，因此复杂度为O(k)，其中k是子树中节点的数量。

现在关于isBalanced。首先计算高度(如前所述，是线性的)。但是如果我们运气不好，我们还需要计算左子树和右子树的isBalanced两次。在最坏情况下，我们要执行log N 次线性计算。

您可以研究主定理，它描述了更一般的情况。

在这种特殊情况下，定理的参数为：a=b=2，并且将问题分解成子问题有恒定的开销。

- Dmitry Kuzminov

---

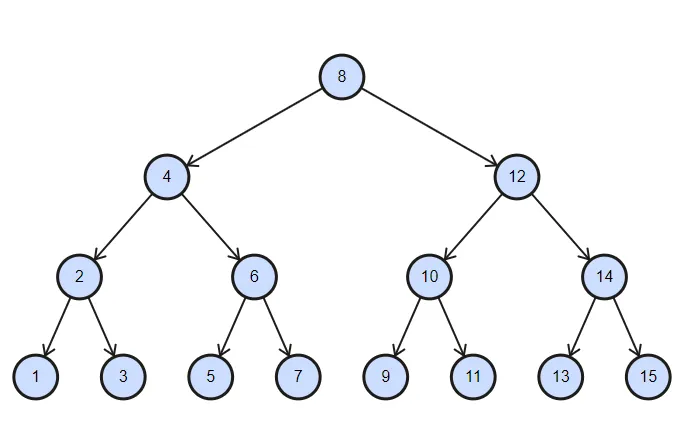
对于一个有n个节点的树，O(子树长度)就是O(n)，对吗？ - David G

不完全是这样。这只是比n小的子问题的长度。但事实上，您将一个较大的问题分成两个大小为一半的不同子问题。最终，n = 1/2n + 1/2n = 1/4n + 1/4n + 1/4n + 1/4n = ... - Dmitry Kuzminov

@0x499602D2 "子树的“长度”是什么？" - Code-Apprentice

@0x499602D2 好的，你在这里澄清了答案的第一句话。我错过了那部分。 - Code-Apprentice

你应该指明最坏情况是什么。对我来说，这是令人困惑的部分。我原以为最坏情况是在最后一层出现不平衡的树，但实际上是完全平衡的树。 - Peter Cheng

Answer 3

该算法的最坏时间复杂度发生在平衡二叉搜索树的情况下，否则我们会提前返回。考虑以下平衡二叉搜索树 。isBalanced函数遍历所有节点一次（包括叶子节点的空子节点）。对于这些节点中的每一个节点，它调用getHeight来计算左右子节点的高度。 因此，getHeight的工作量与该节点为根的子树的大小成比例。
对于叶节点的空子节点（有16个这样的节点），它需要恒定数量的工作。 对于叶子节点(1, 3, 5, 7 ...)，我们需要两倍的工作量，但是我们的节点减少了一半（即我们有8个节点）。 在上面一级，我们需要四倍的工作量，但是我们的节点再次减半。
通常，如果我们有N个节点，则总工作量大约为

N + N/2*2 + N/4*4 + ... + N/N * 1

每个求和项都等于N。有多少个这样的项？这就是树的高度，即lg(N)，因为我们将N除以2直到它达到1。因此，总复杂度为O(N*lg(N))。

- xashru

---

所以O(logN)是因为我们最多需要O(logN)个递归调用，因为我们可能需要递归到树的深度？ - Jessica

Answer 4

在正式的定义中，如果我们假设 getHeight 的复杂度是 G(n)，isBalance 函数的复杂度是 T(n)，那么我们将有 G(n) = G(n1) + G(n2) + 1 和 T(n) = T(n1) + T(n2) + G(n) + 1，其中 n1 是左子树的大小，n2 是右子树的大小，且 n1 + n2 = n - 1。

尝试扩展 G(n) = (G(n11) + G(n12) + 1) + (G(n21)+G(n22) + 1) + 1，使得 n11 + n12 + n21 + n22 = n1 - 1 + n2 - 1 = n - 3。因此，G(n) = G(n11) + G(n12) + G(n21) + G(n22) + 3。使用归纳法，我们可以发现 G(n) = Theta(n)。因此，我们有 T(n) = T(n1) + T(n2) + \Theta(n) + 1。

现在，如果子树高度差大于1，则算法将返回false并终止，最坏情况是|log(n2) - log(n1)| <= 1（log(n{i})是子树的高度）。因此，通过求平方2，我们有n2/n1 <= 2。这意味着n1和n2是n的一个常数因子，因为n1 + n2 = n -1。现在，从Akra-Bazzi定理，通过p = 1（近似值），以及g(n) = n（因为它是\Theta(n)），在最坏情况下，T(n)的复杂度为n*(1 + integral(x/x^2, 1, n)) = n*(1 + integral(1/x, 1, n) = n * (1 + log(n))。因此，T(n) = O(n log(n))。

- OmG