TLDR： 如果您已经熟悉本主题的问题及到目前为止提供的答案，请跳至下面的“ClosestPair启发式方法的明确说明”部分。
备注： 我最近开始阅读《算法设计手册》，但是其中的 ClosestPair 启发式例子让我感到不太清晰。看起来其他人也有类似的感觉。不幸的是，这个主题上提供的答案对我来说都有点含糊和笼统。但这些答案确实帮助我朝着我认为是Skiena的正确解释方向推进。
问题陈述和背景： 对于没有此书的人（第三版），从书的第5页开始:
Skiena首先详细介绍了NearestNeighbor启发式算法的不正确性，使用以下图片来帮助说明他的论点：
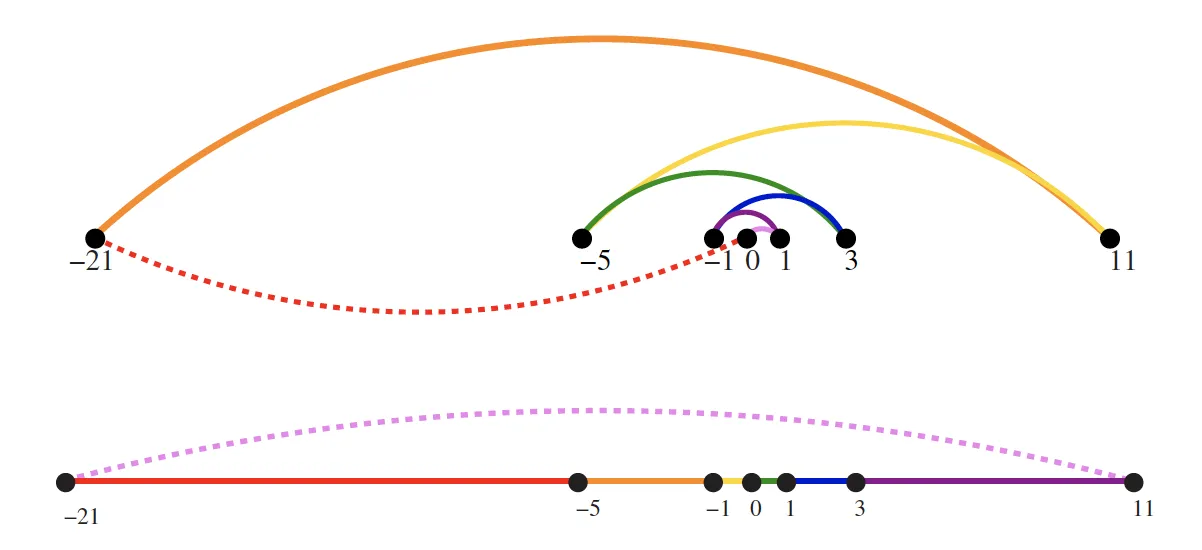
上面的图表描绘了NearestNeighbor启发式方法所采用的问题，而下面的图表则是最优解。显然，需要采用不同的方法来找到这个最优解。这就引出了ClosestPair启发式方法以及这个问题的原因。
书籍描述：关于ClosestPair启发式方法的以下描述在书中被概述：
也许我们需要一种不同的方法来处理最近邻启发式算法中被证明是坏实例的情况。总是走向最近的点太过严格，因为这似乎会让我们陷入我们不想要的移动中。
另一个想法可能是重复连接最接近的一对端点，其连接不会创建问题，例如循环的过早终止。每个顶点都作为自己的单个顶点链开始。将所有东西合并在一起后，我们最终会得到一个包含其中所有点的单个链。连接最终的两个端点会给我们一个循环。在执行这个最近对启发式算法的任何步骤中，我们将有一组可用于合并的单个顶点和顶点不相交链的末尾。实现此描述的伪代码如下所示。
ClosestPair 启发式算法的澄清描述
首先，我们可以“放大”一点，回答一个基本问题，即在图论术语中我们要找到什么：
什么是最短的闭合路径？
也就是说，我们想要找到一系列边 (e_1, e_2, ..., e_{n-1})，其中有一个顶点序列 (v_1, v_2, ..., v_n)，满足 v_1 = v_n 且所有边都不同。这些边都有权重，每条边的权重都是组成该边的顶点之间的距离 - 我们希望尽可能减小任何闭合路径的总权重。
实际上，ClosestPair启发式算法为我们提供了每次外部for循环迭代（代码行3-10）中的一个这些不同的边缘，其中内部for循环（代码行5-9）确保在每个步骤选择不同的边缘(s_m, t_m)，由来自不同顶点链的端点组成；也就是说，s_m来自一个顶点链的端点，而t_m来自另一个不同的顶点链的端点。内部for循环只是确保我们考虑所有这样的对，在此过程中最小化潜在顶点之间的距离。
注意（顶点之间距离相等的情况）：一个潜在的混淆源是，在任何一个for循环中都没有指定任何“处理顺序”。我们如何确定比较端点和这些端点的顶点的顺序？这并不重要。内部for循环的性质表明，在距离相等的情况下，选择最近遇到的具有最小距离的顶点配对。
ClosestPair启发式算法的良好实例
回想一下在应用NearestNeighbor启发式算法时发生的“坏实例”（请注意新添加的顶点标签）：
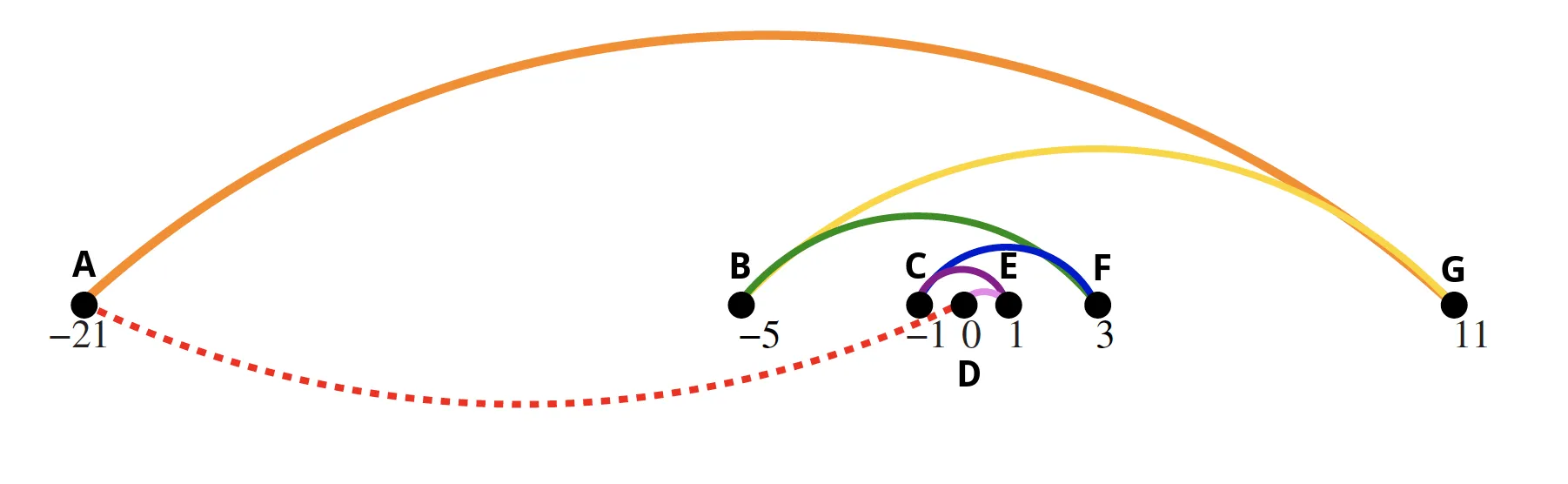
总距离很荒谬，因为我们一直在0上下跳动。
现在考虑使用ClosestPair启发式算法时会发生什么。我们有n = 7个顶点；因此，伪代码表明外部的for循环将被执行6次。正如书中所述，每个顶点最初都是自己的单个顶点链（即每个点都是一个单点，其中单点是具有一个端点的链）。在我们的情况下，鉴于上面的图，内部的for循环将执行多少次？嗯，从n个元素集合中选择一个2元素子集的方法有多少种（即2元素子集表示潜在的顶点配对）？有n choose 2这样的子集：
!%7D=%5Cfrac%7Bn(n-1)%7D%7B2%7D "https://latex.codecogs.com/png.image?\dpi{110}\bg{white}\binom{n}{2}=\frac{n!}{2!(n-2)!}=\frac{n(n-1)}{2}")
由于在我们的情况下 n = 7，因此有总共21种可能的顶点配对需要研究。上图的性质清楚地表明，由于开始时顶点之间的最小距离为1且 dist(C, D) = dist(D, E) = 1，因此 (C, D) 和 (D, E) 是第一次迭代的唯一可能结果。哪些顶点实际上连接起来形成了第一条边 (C, D) 或者 (D, E) 是不清楚的，因为没有处理顺序。假设我们最后遇到顶点 D 和 E，因此导致 (D, E) 成为我们的第一条边。
现在还有5次迭代和6个顶点链需要考虑：A, B, C, (D, E), F, G。
注意（每次迭代都会消除一个顶点链）：在ClosestPair启发式的外部for循环的每次迭代中，都会消除一个顶点链。外部for循环迭代将继续进行，直到我们只剩下一个由所有顶点组成的单个顶点链，最后一步是通过边连接这个单个顶点链的两个端点。更准确地说，对于由n个顶点组成的图G，我们从n个顶点链开始（即，每个顶点都作为自己的单个顶点链）。外部for循环的每次迭代都会连接G的两个顶点，使得这些顶点来自不同的顶点链; 也就是说，连接这些顶点会将两个不同的顶点链合并成一个，从而将要考虑的顶点链总数减少1。对于具有n个顶点的图进行n-1次重复此过程将导致只剩下一个包含G所有点的单一链，即n-(n-1)=1个顶点链。连接最终的两个端点会给我们一个循环。
每个迭代的可能表现如下：
ClosestPair outer for loop iterations
1: connect D to E # -> dist: 1, chains left (6): A, B, C, (D, E), F, G
2: connect D to C # -> dist: 1, chains left (5): A, B, (C, D, E), F, G
3: connect E to F # -> dist: 3, chains left (4): A, B, (C, D, E, F), G
4: connect C to B # -> dist: 4, chains left (3): A, (B, C, D, E, F), G
5: connect F to G # -> dist: 8, chains left (2): A, (B, C, D, E, F, G)
6: connect B to A # -> dist: 16, single chain: (A, B, C, D, E, F, G)
Final step: connect A and G
因此，在这个示例中，
ClosestPair启发式方法做出了正确的决策，而之前的
NearestNeighbor启发式方法则做出了错误的决策。
ClosestPair启发式算法的错误实例
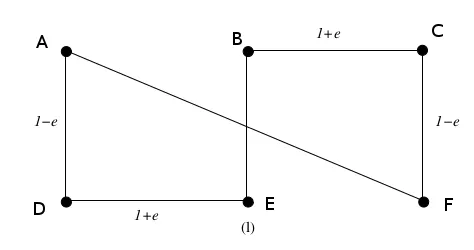
考虑下面图中点集上ClosestPair算法的执行情况（首先尝试想象没有任何边连接顶点的点集可能会有所帮助）：
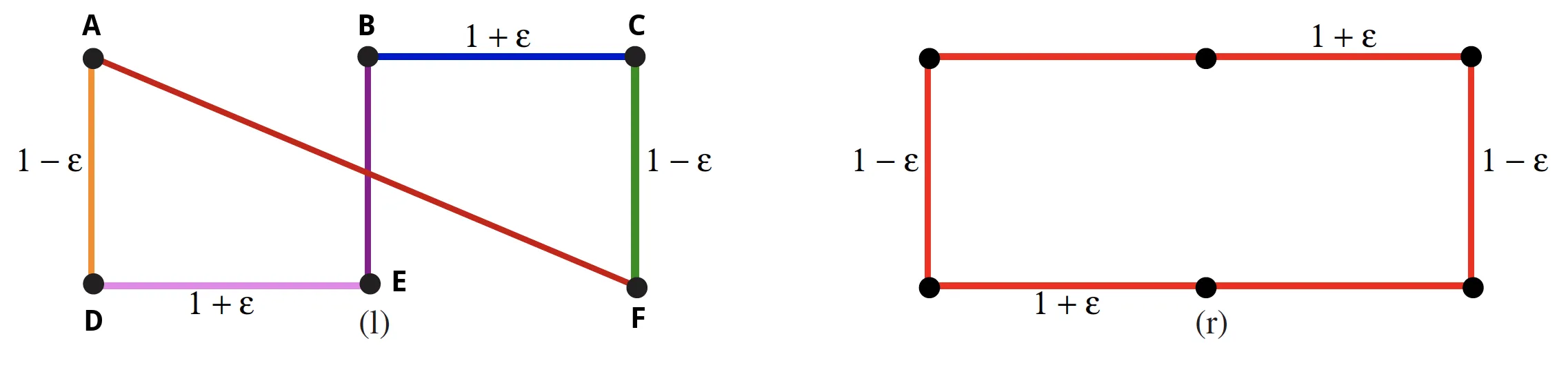
我们如何使用
ClosestPair连接顶点？我们有
n = 6个顶点；因此，外部的
for循环将执行
6-1=5次，我们首先要做的是研究顶点之间的距离。
!%7D=%5Cfrac%7B6%5Ccdot&space;5%7D%7B2%7D=15 "https://latex.codecogs.com/png.image?\dpi{110}\bg{white}\binom{6}{2}=\frac{6!}{2!(6-2)!}=\frac{6\cdot 5}{2}=15")
总可能的配对数。上面的图表帮助我们看到，在第一次迭代中，dist(A, D) = dist(B, E) = dist(C, F) = 1 - ɛ 是唯一可能的选项，因为1 - ɛ是任意两个顶点之间最短的距离。我们随意选择(A, D)作为第一个配对。
现在还有4次迭代和5个顶点链需要考虑：(A, D), B, C, E, F。每次迭代的可能描述如下：
ClosestPair outer for loop iterations
1: connect A to D # --> dist: 1-ɛ, chains left (5): (A, D), B, C, E, F
2: connect B to E # --> dist: 1-ɛ, chains left (4): (A, D), (B, E), C, F
3: connect C to F # --> dist: 1-ɛ, chains left (3): (A, D), (B, E), (C, F)
4: connect D to E # --> dist: 1+ɛ, chains left (2): (A, D, E, B), (C, F)
5: connect B to C # --> dist: 1+ɛ, single chain: (A, D, E, B, C, F)
Final step: connect A and F
注意（正确考虑连接不同顶点链的端点）：上面所示的迭代1-3在某种意义上是相当平淡无奇的，因为我们没有其他有意义的选择。即使我们已经有了不同的顶点链(A, D)、(B, E)和(C, F)，下一个选择也同样平淡无奇且任意。由于第四次迭代中顶点之间的最小距离是1 + ɛ，因此有四种可能性：(A, B), (D, E), (B, C), (E, F)。以上所有点之间的距离都是1 + ɛ。选择(D, E)是任意的。其他三个顶点配对中的任何一个都可以同样有效地工作。但请注意，在第5次迭代期间会发生什么——我们的顶点配对选择范围已经被严格缩小。具体来说，顶点链(A, D, E, B)和(C, F)，它们的端点分别为(A, B)和(C, F)，只允许四种可能的顶点配对：(A, C), (A, F), (B, C), (B, F)。即使这似乎是显而易见的，值得明确指出的是，D和E都不是上述可行的顶点候选——它们都没有包含在它们是顶点的顶点链的端点(A, D, E, B)中的端点(A, B)中。此时没有任意选择。以上配对中顶点之间的距离没有平局。(B, C)配对结果产生了顶点之间最小的距离：1 + ɛ。一旦顶点B和C被边连接，所有迭代都已完成，我们只剩下一个顶点链：(A, D, E, B, C, F)。连接A和F会给我们一个循环并结束整个过程。
在 (A, D, E, B, C, F) 路线上的总行程如下：
%7D_%7B%5Ctexttt%7BA%7D%5Cto%5Ctexttt%7BD%7D%7D&space;+%5Cunderbrace%7B(1+%5Cvarepsilon)%7D_%7B%5Ctexttt%7BD%7D%5Cto%5Ctexttt%7BE%7D%7D&space;+%5Cunderbrace%7B(1-%5Cvarepsilon)%7D_%7B%5Ctexttt%7BE%7D%5Cto%5Ctexttt%7BB%7D%7D&space;+%5Cunderbrace%7B(1+%5Cvarepsilon)%7D_%7B%5Ctexttt%7BB%7D%5Cto%5Ctexttt%7BC%7D%7D&space;+%5Cunderbrace%7B(1-%5Cvarepsilon)%7D_%7B%5Ctexttt%7BC%7D%5Cto%5Ctexttt%7BF%7D%7D&space;+%5Cunderbrace%7B%5Csqrt%7B(1-%5Cvarepsilon)%5E2+(2+2%5Cvarepsilon)%5E2%7D%7D_%7B%5Ctexttt%7BF%7D%5Cto%5Ctexttt%7BA%7D%7D "https://latex.codecogs.com/png.image?\dpi{110}\bg{white}\underbrace{(1-\varepsilon)}_{\texttt{A}\to\texttt{D}} +\underbrace{(1+\varepsilon)}_{\texttt{D}\to\texttt{E}} +\underbrace{(1-\varepsilon)}_{\texttt{E}\to\texttt{B}} +\underbrace{(1+\varepsilon)}_{\texttt{B}\to\texttt{C}} +\underbrace{(1-\varepsilon)}_{\texttt{C}\to\texttt{F}} +\underbrace{\sqrt{(1-\varepsilon)^2+(2+2\varepsilon)^2}}_{\texttt{F}\to\texttt{A}}")
上述距离计算结果为5 - ɛ + √(5ɛ^2 + 6ɛ + 5)，而不是仅绕边界行驶的总路程（上图中右侧的所有边缘均为红色）：6 + 2ɛ。当ɛ -> 0时，我们可以看到5 + √5 ≈ 7.24 > 6，其中6是必要的行驶距离。因此，我们最终行驶的距离约为
-6%7D%7B6%7D%5Ctimes&space;100%5Capprox&space;20.6%5C% "https://latex.codecogs.com/png.image?\dpi{110}\bg{white}\frac{(5+\sqrt{5})-6}{6}\times 100\approx 20.6\%")
在这种情况下使用ClosestPair启发式方法会比必要的更进一步。
