首先,我会提醒我们如何找到多边形的面积。一旦我们做到了这一点,就可以很容易地理解在多边形和圆之间找到交点的算法。
如何找到多边形的面积
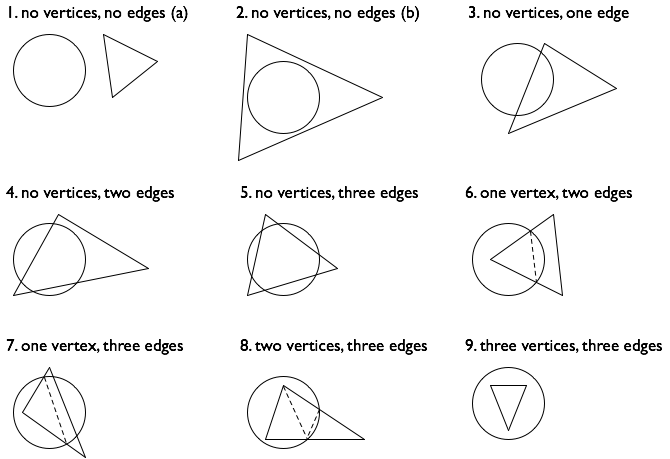
让我们看一个三角形的情况,因为所有必要的逻辑都在那里。假设我们有一个三角形,其顶点为(x1,y1)、(x2,y2)和(x3,y3),当您沿着三角形逆时针方向移动时,如下图所示:
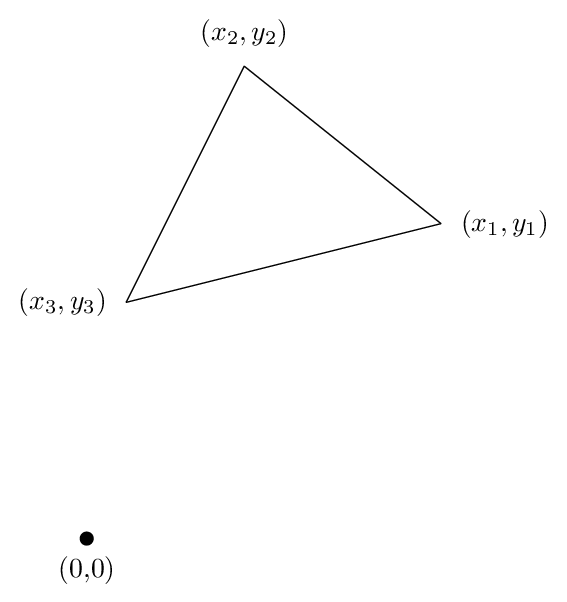
然后,您可以通过公式计算面积
A=(x1 y2 + x2 y3 + x3 y1 - x2y1- x3 y2 - x1y3)/2.
为了看清楚这个公式是如何工作的,让我们重新排列它,使其呈现为以下形式
A=(x1 y2 - x2 y1)/2 + (x2 y3 - x3 y2)/2 + (x3 y1 - x1y3 )/2。
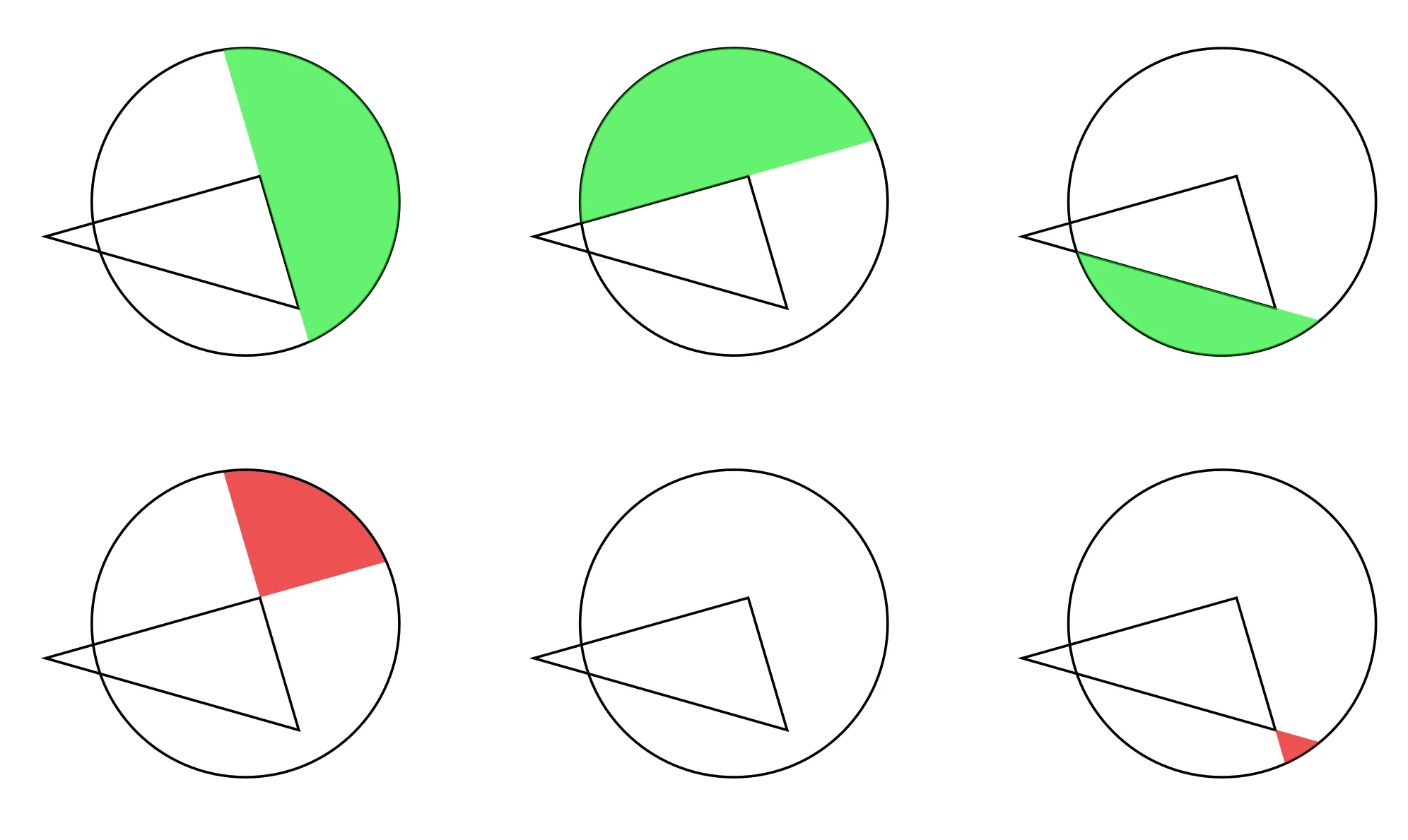
现在第一个术语是以下区域,这在我们的情况下是正的:
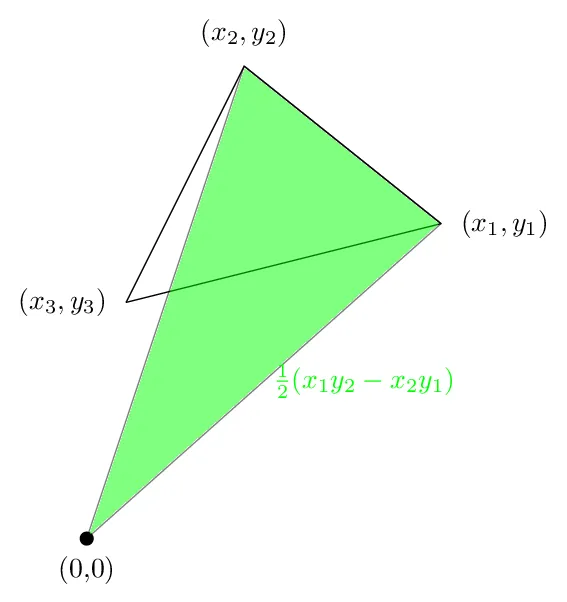
如果不清楚绿色区域的面积确实是(x1 y2-x2 y1)/ 2,则阅读this。
第二个术语是这个区域,这又是正的:
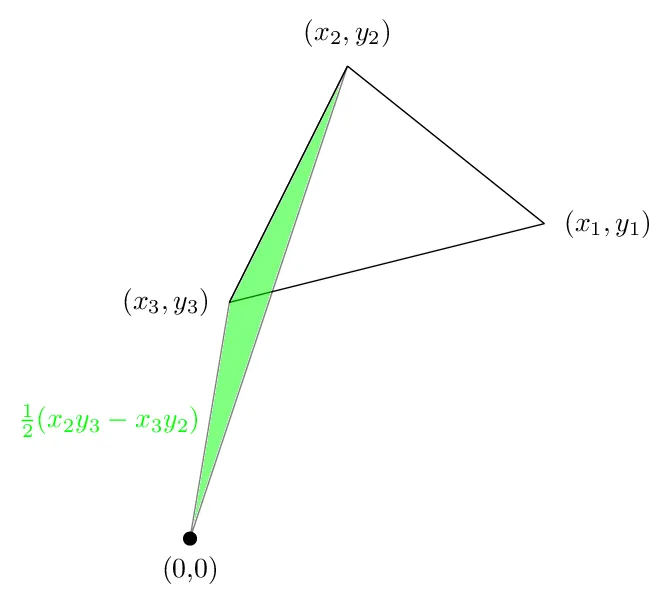
第三个区域如下图所示。这次的面积是负数。
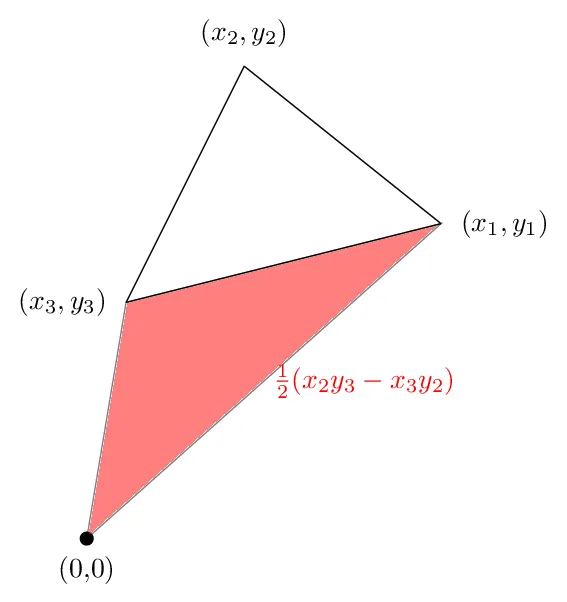
把这三个数加起来,我们得到以下的图片
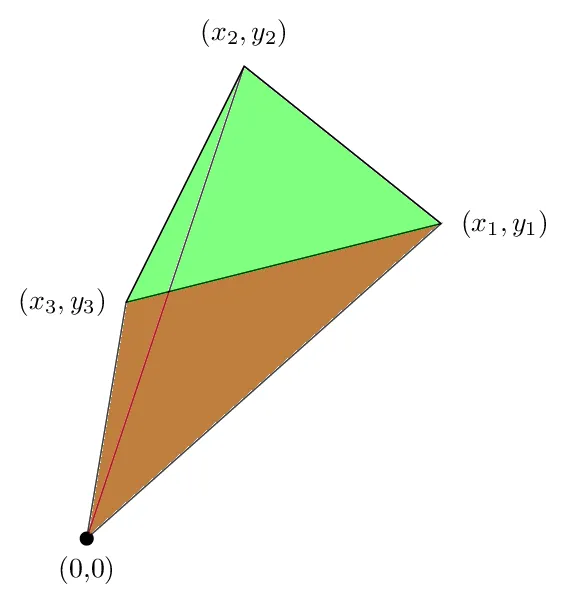
我们看到,原先在三角形外的绿色区域被红色区域抵消了,因此净面积就是三角形的面积,这说明为什么这个公式在这种情况下是正确的。
上述内容是关于面积公式正确的直观解释。更严谨的解释是观察到当我们从一条边计算面积时,我们得到的面积与通过积分r^2dθ/2得到的面积相同,因此我们实际上是在多边形边界周围积分r^2dθ/2,并根据斯托克斯定理,这给出与在多边形边界周围积分rdrdθ得到的结果相同。由于在多边形所围区域上积分rdrdθ给出的是面积,因此我们得出结论:我们的过程必须正确地给出面积。
圆与多边形的交集面积
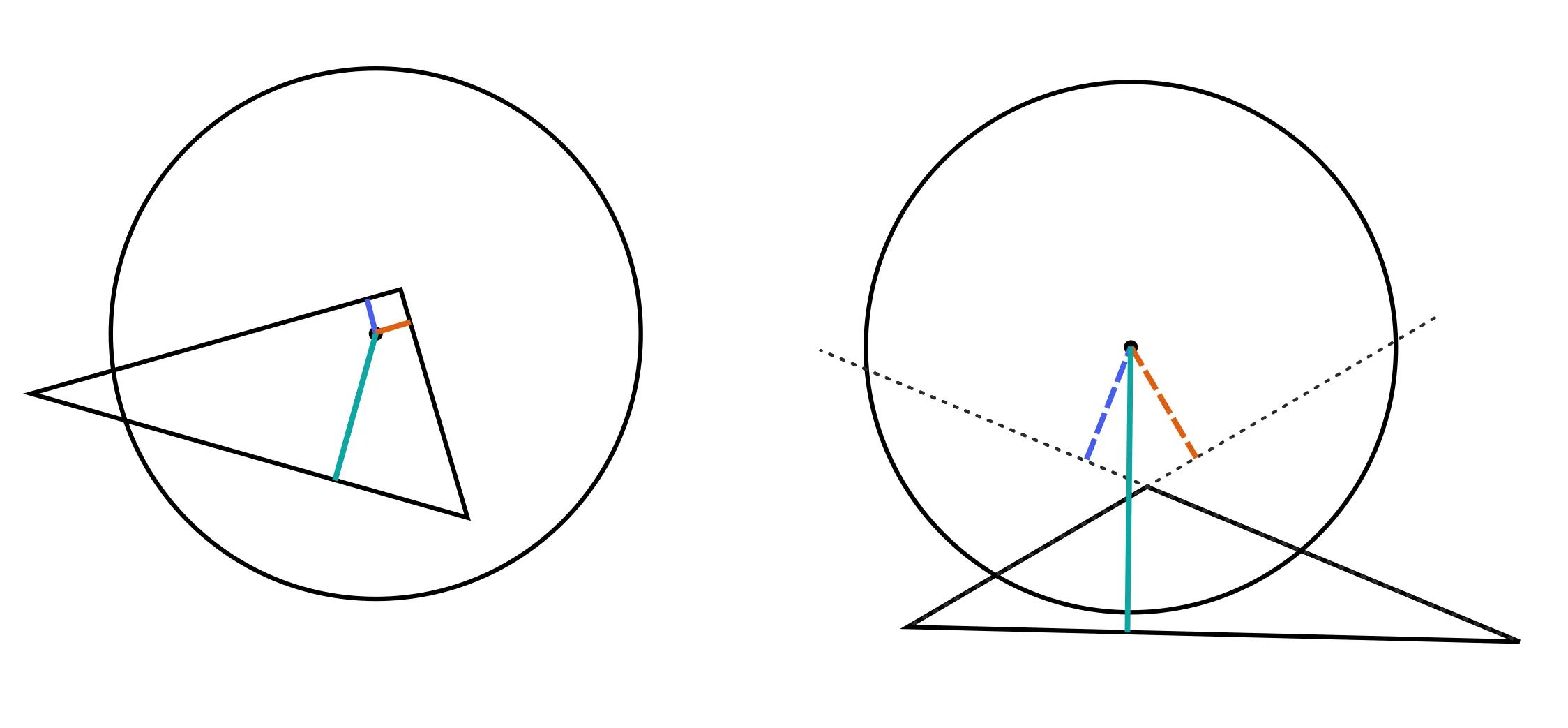
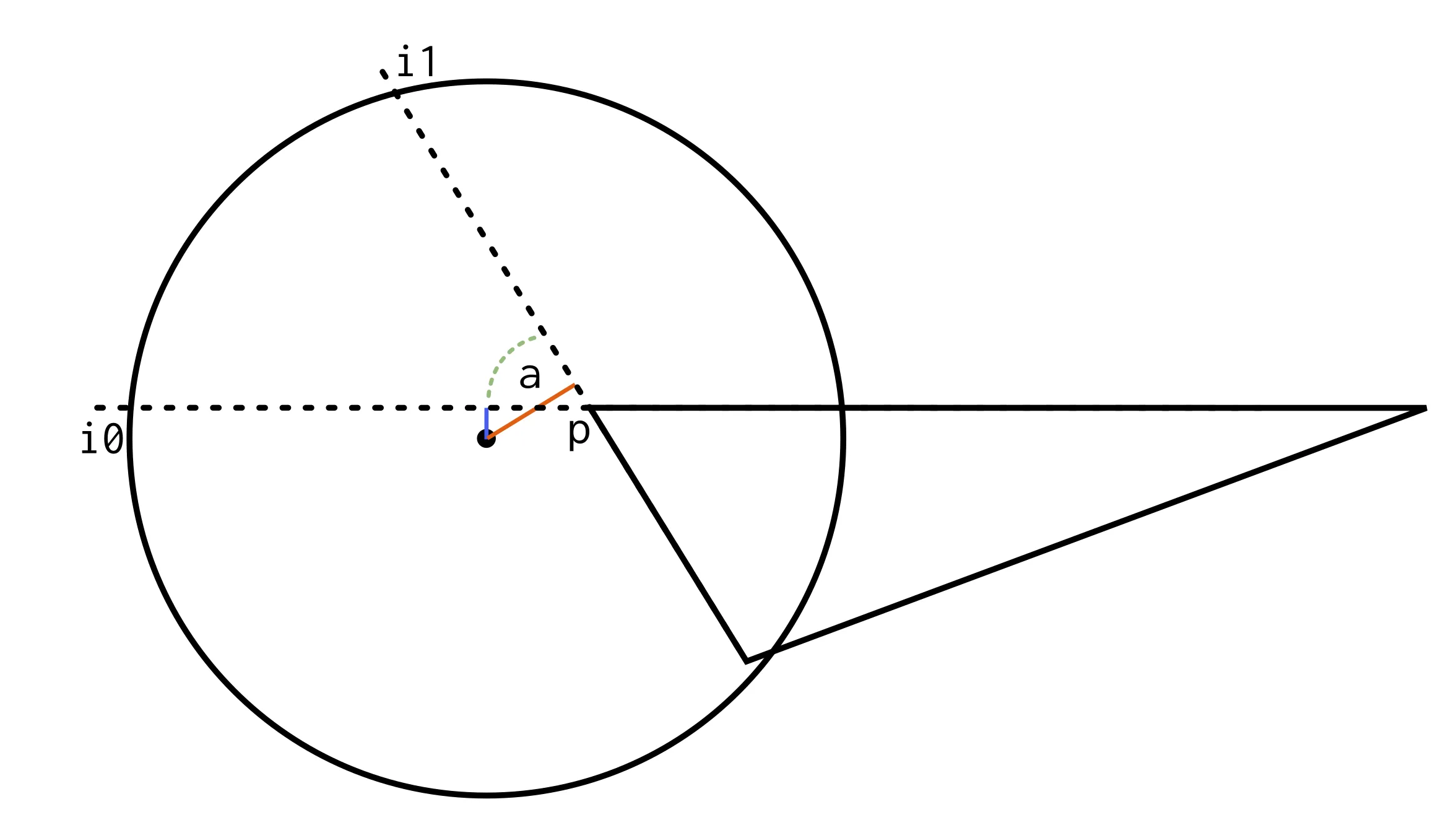
现在让我们讨论如何找到半径为R的圆与多边形的交集面积,如下图所示:
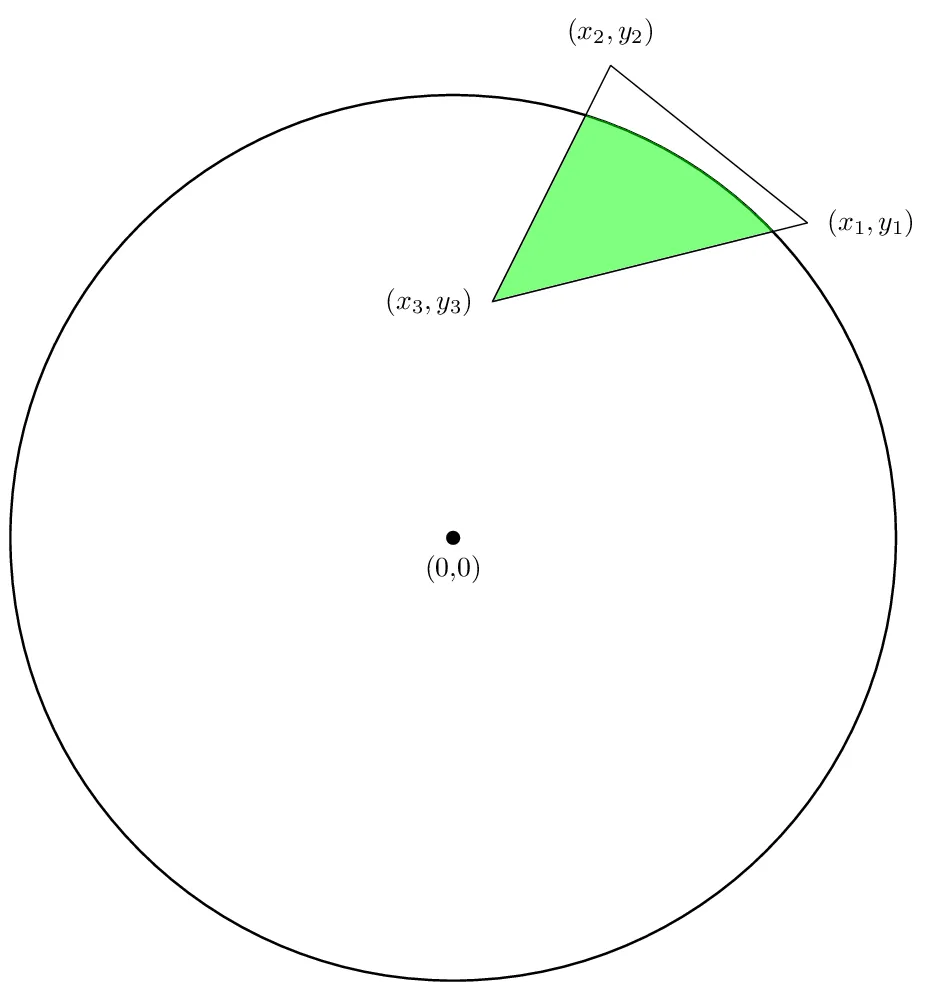
我们对找到绿色区域的面积感兴趣。就像单个多边形的情况一样,我们可以将计算分解为查找多边形每条边的面积,然后将这些面积相加。
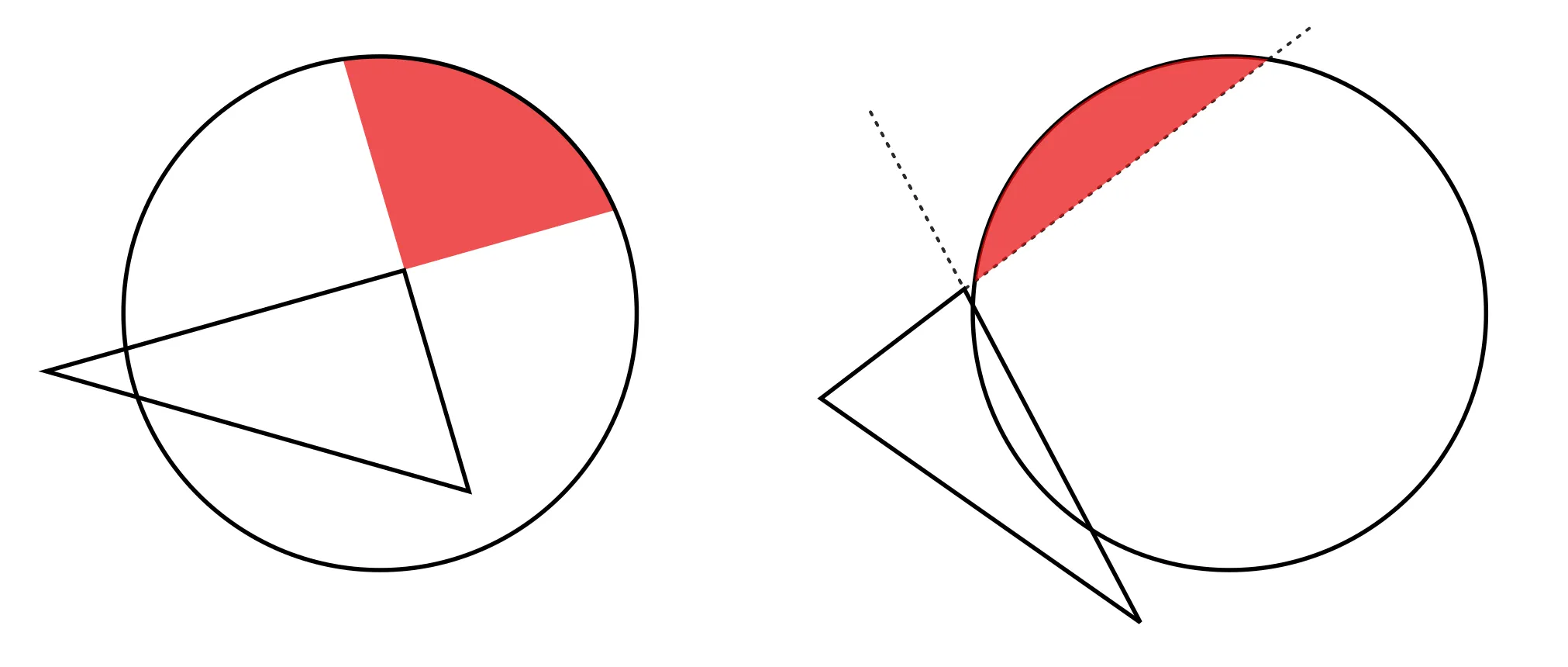
我们的第一个面积将如下所示:
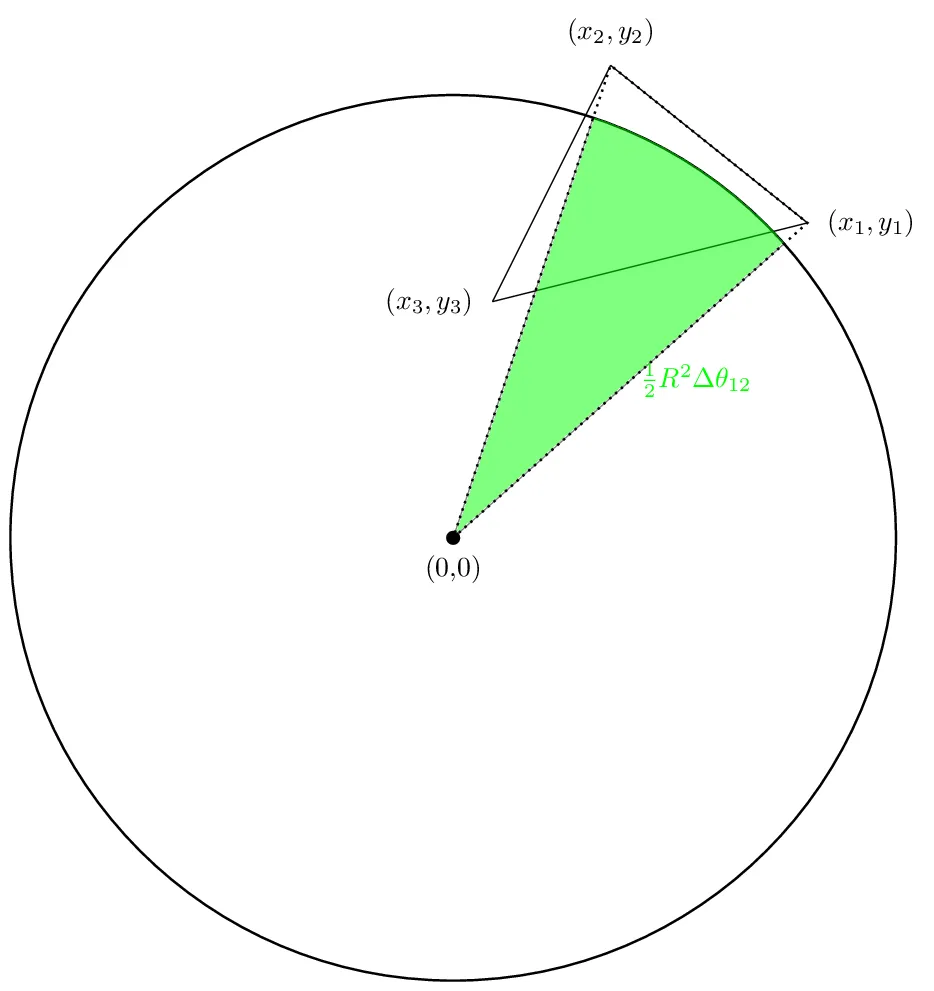
第二个区域看起来会像这样
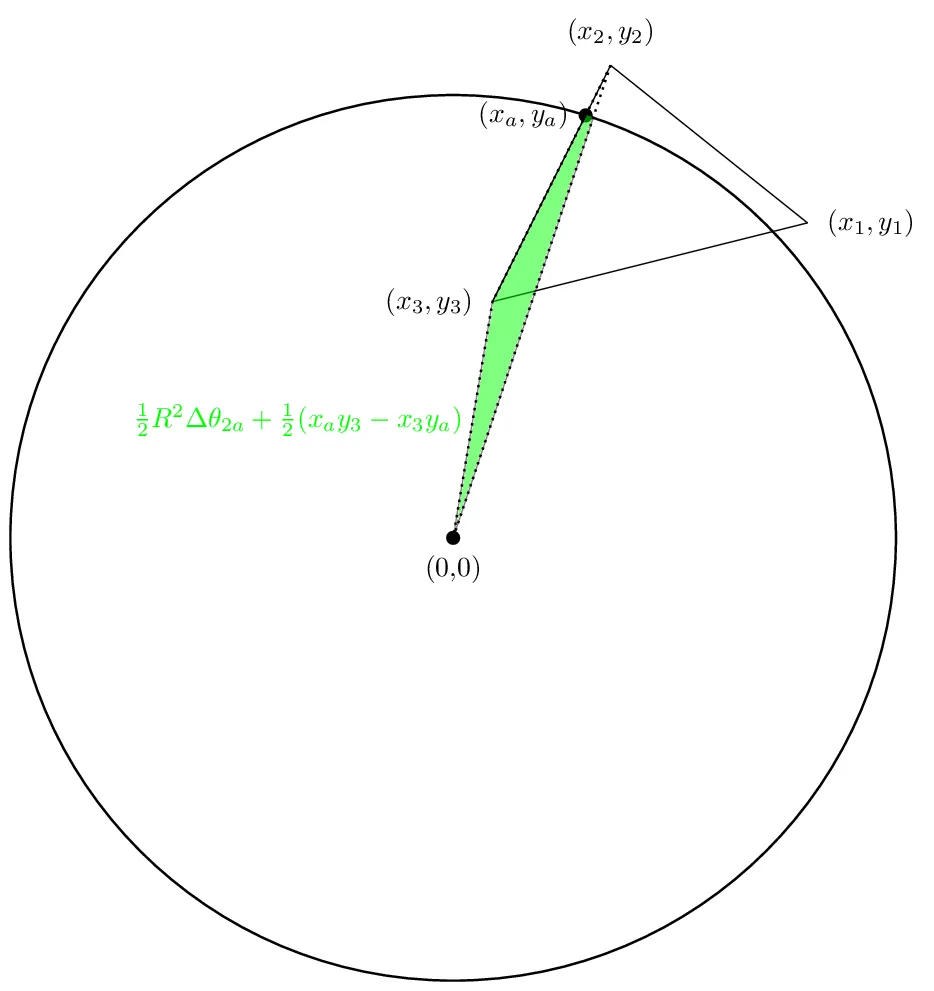
第三个区域将是
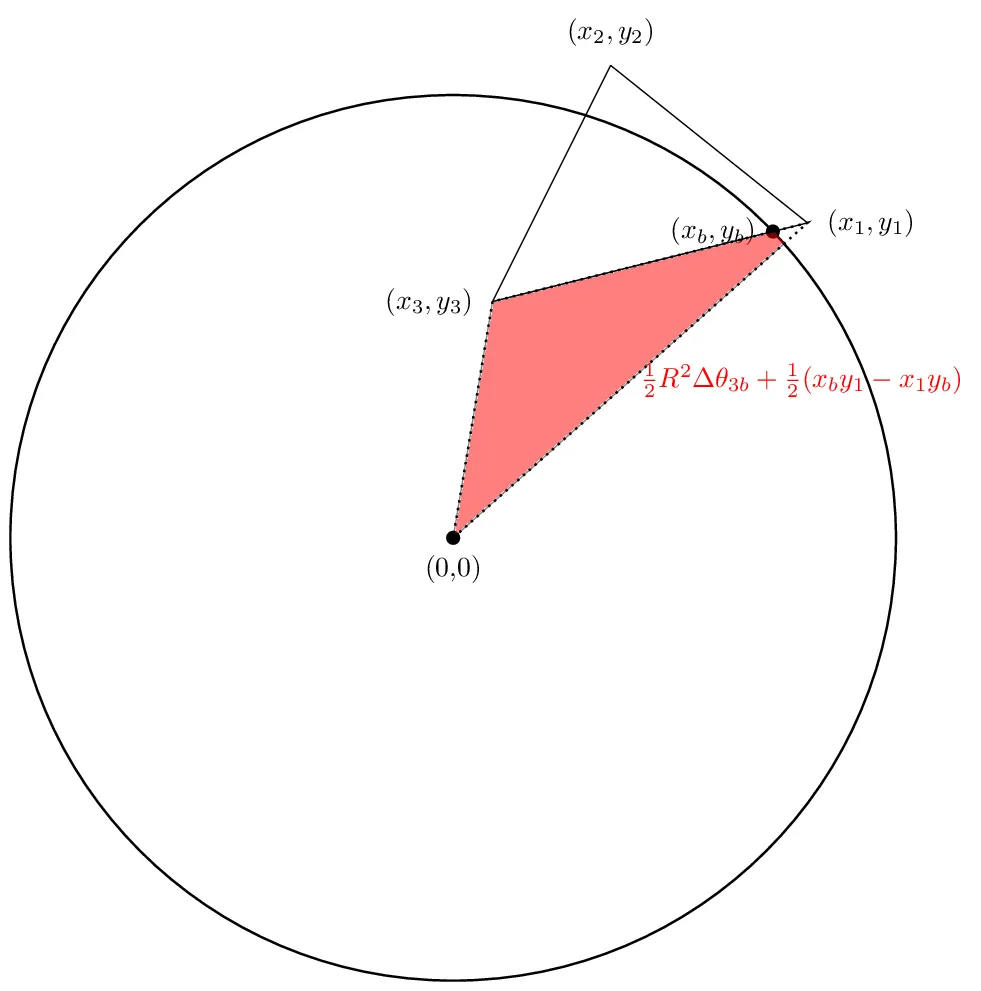
同样,在我们的情况下,前两个区域是正的,而第三个区域将是负的。希望取消将起作用,以便净面积确实是我们感兴趣的面积。让我们看看。
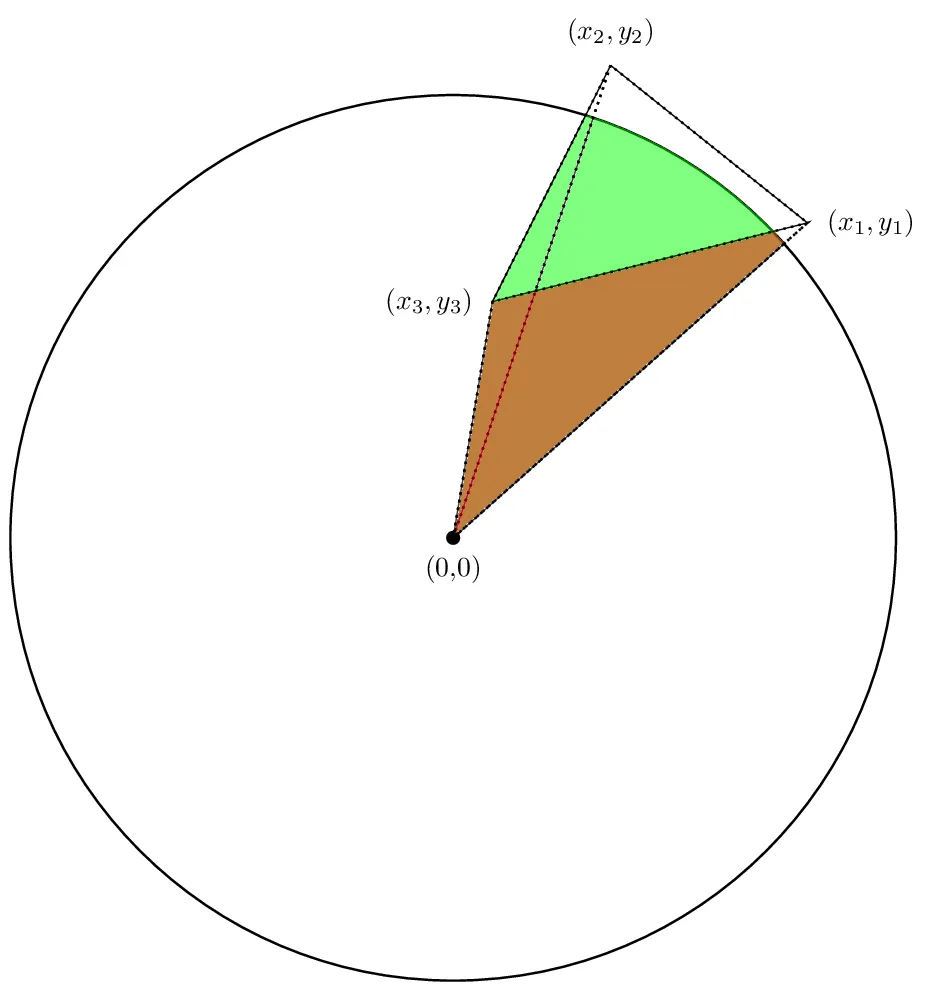
实际上,所有面积的总和将是我们感兴趣的区域的面积。
同样,我们可以更严谨地解释为什么这样做有效。设I为交集定义的区域,P为多边形。然后根据前面的讨论,我们知道要计算围绕I边界的r^2dθ/2的积分。但是,这很难做到,因为它需要找到交点。
相反,我们对多边形进行了积分。我们在多边形边界上积分max(r,R)^2 dθ/2。为了看到为什么这会得出正确的答案,让我们定义一个函数π,它将极坐标(r,θ)中的点转换为点(max(r,R),θ)。引用π(r)=max(r,R)和π(θ)=θ的坐标函数不应该让人感到困惑。然后我们所做的就是在多边形边界上积分π(r)^2 dθ/2。
另一方面,由于π(θ)=θ,这与在多边形边界上积分π(r)^2 dπ(θ)/2相同。
现在进行变量替换,我们发现如果在π(P)的边界上积分r^2 dθ/2,其中π(P)是P在π下的图像,则会得到相同的答案。
再次使用Stokes定理,我们知道在π(P)的边界上积分r^2 dθ/2可以给我们π(P)的面积。换句话说,它和在π(P)上积分dxdy得到的答案是一样的。
再次使用变量转换,我们知道在π(P)上积分dxdy和在P上积分Jdxdy是相同的,其中J是π的雅可比矩阵。
现在我们可以将Jdxdy的积分分为两个区域:圆内和圆外。 π会保留圆内的点,因此在那里J=1,所以来自P的这部分的贡献是P在圆内的部分的面积,即交集的面积。第二个区域是圆外的区域。在那里,由于π将该部分压缩到圆的边界上,J=0。
因此,我们计算的确实是交集的面积。
现在我们相对确定如何概念化地找到该区域的面积,让我们更具体地讨论如何计算单个线段的贡献。让我们从“标准几何”中的一个线段开始看起。如下所示:
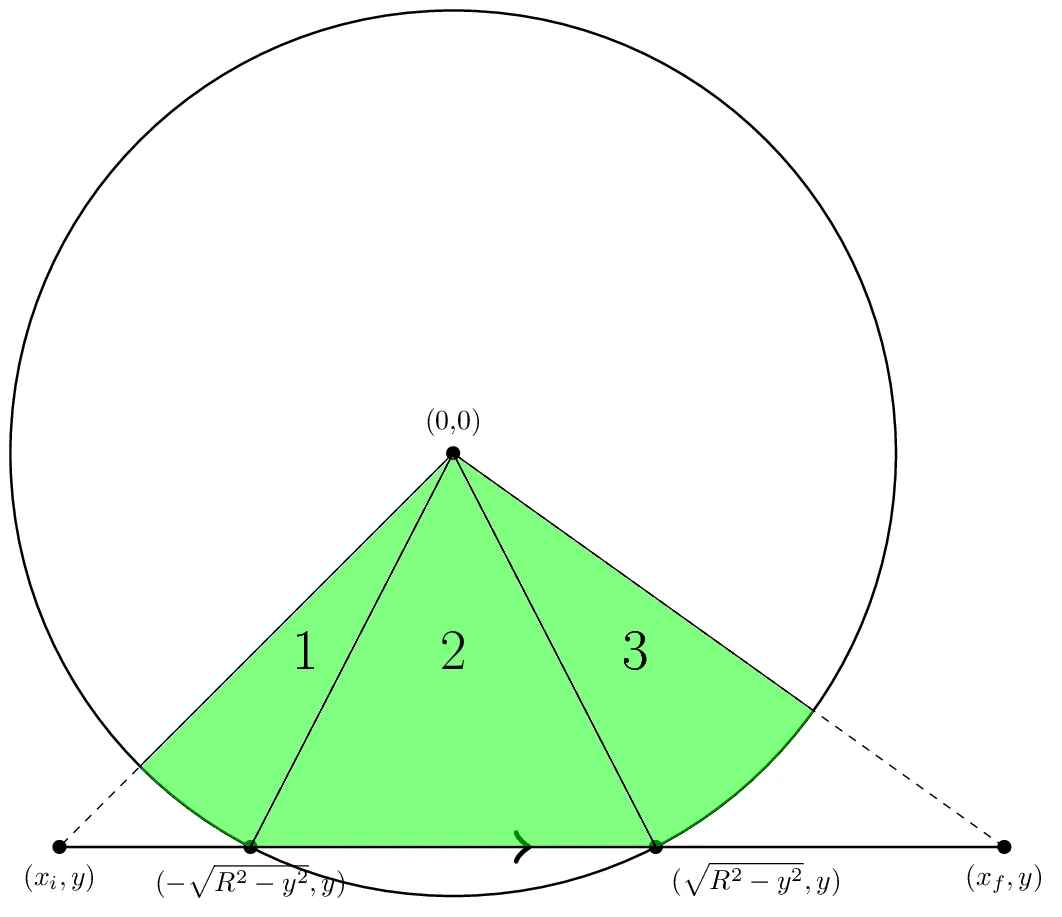
在标准几何中,边缘从左到右水平延伸。它由三个数字描述:xi,边缘开始的x坐标,xf,边缘结束的x坐标,以及y,边缘的y坐标。
现在我们看到,如果|y| < R,如图所示,则边缘将在点(-xint,y)和(xint,y)处与圆相交,其中xint = (R^2-y^2)^(1/2)。然后,我们需要计算的区域分为图中标记的三个部分。要获得区域1和3的面积,我们可以使用arctan获取各个点的角度,然后将面积等于R^2 Δθ/2。例如,我们将设置θi = atan2(y,xi)和θl = atan2(y,-xint)。然后,区域一的面积为R^2(θl-θi)/2。我们可以类似地获得区域3的面积。
区域2的面积只是一个三角形的面积。但是,我们必须小心符号。我们希望显示的区域面积为正,因此我们将该面积表示为-(xint - (-xint))y/2。
需要记住的另一件事是,通常情况下,xi不必小于-xint,xf也不必大于xint。
另一个要考虑的情况是|y| > R。这种情况更简单,因为只有一个与图中区域1类似的部分。
现在我们知道如何从标准几何中的边缘计算面积,唯一剩下的就是描述如何将任何边缘转换为标准几何。
但这只是一个简单的坐标变换。给定一些具有初始顶点vi和最终顶点vf的内容,新的x单位向量将是从vi指向vf的单位向量。然后,xi只是从圆心到x点的位移与vi的位移相乘,xf只是xi加上vi和vf之间的距离。同时,y由x与vi到圆心的位移的楔积给出。
代码
算法的描述完成了,现在是编写代码的时候了。我将使用Java。
首先,由于我们正在处理圆形,因此应该有一个圆形类。
public class Circle {
final Point2D center;
final double radius;
public Circle(double x, double y, double radius) {
center = new Point2D.Double(x, y);
this.radius = radius;
}
public Circle(Point2D.Double center, double radius) {
this(center.getX(), center.getY(), radius);
}
public Point2D getCenter() {
return new Point2D.Double(getCenterX(), getCenterY());
}
public double getCenterX() {
return center.getX();
}
public double getCenterY() {
return center.getY();
}
public double getRadius() {
return radius;
}
}
对于多边形,我将使用Java的
Shape类。
Shape具有
PathIterator,我可以使用它来迭代多边形的边缘。
现在是实际工作的时候了。我将把迭代边缘、将边缘放入标准几何图形等逻辑与计算完成后的面积逻辑分开。原因是您将来可能想要计算除面积以外或者除面积之外的其他内容,您希望能够重用处理迭代边缘的代码。
因此,我有一个通用类,它计算关于我们的多边形圆形交集的类
T的某些属性。
public abstract class CircleShapeIntersectionFinder<T> {
它有三个静态方法,只是帮助计算几何图形:
private static double[] displacment2D(final double[] initialPoint, final double[] finalPoint) {
return new double[]{finalPoint[0] - initialPoint[0], finalPoint[1] - initialPoint[1]};
}
private static double wedgeProduct2D(final double[] firstFactor, final double[] secondFactor) {
return firstFactor[0] * secondFactor[1] - firstFactor[1] * secondFactor[0];
}
static private double dotProduct2D(final double[] firstFactor, final double[] secondFactor) {
return firstFactor[0] * secondFactor[0] + firstFactor[1] * secondFactor[1];
}
有两个实例字段,一个是Circle,它只是保留圆的副本,另一个是currentSquareRadius,它保留正方形半径的副本。这可能看起来很奇怪,但我使用的类实际上可以找到整个圆形多边形交集的面积。这就是为什么我将其中一个圆称为“当前”的原因。
private Circle currentCircle;
private double currentSquareRadius;
接下来是计算我们想要计算的方法:
public final T computeValue(Circle circle, Shape shape) {
initialize();
processCircleShape(circle, shape);
return getValue();
}
initialize()和getValue()是抽象的。 initialize()会将保存面积总和的变量设置为零,而getValue()只会返回面积。 processCircleShape的定义如下:
private void processCircleShape(Circle circle, final Shape cellBoundaryPolygon) {
initializeForNewCirclePrivate(circle);
if (cellBoundaryPolygon == null) {
return;
}
PathIterator boundaryPathIterator = cellBoundaryPolygon.getPathIterator(null);
double[] firstVertex = new double[2];
double[] oldVertex = new double[2];
double[] newVertex = new double[2];
int segmentType = boundaryPathIterator.currentSegment(firstVertex);
if (segmentType != PathIterator.SEG_MOVETO) {
throw new AssertionError();
}
System.arraycopy(firstVertex, 0, newVertex, 0, 2);
boundaryPathIterator.next();
System.arraycopy(newVertex, 0, oldVertex, 0, 2);
segmentType = boundaryPathIterator.currentSegment(newVertex);
while (segmentType != PathIterator.SEG_CLOSE) {
processSegment(oldVertex, newVertex);
boundaryPathIterator.next();
System.arraycopy(newVertex, 0, oldVertex, 0, 2);
segmentType = boundaryPathIterator.currentSegment(newVertex);
}
processSegment(newVertex, firstVertex);
}
让我们花一点时间快速查看
initializeForNewCirclePrivate。 这个方法只是设置实例字段,允许派生类存储圆的任何属性。它的定义是:
private void initializeForNewCirclePrivate(Circle circle) {
currentCircle = circle;
currentSquareRadius = currentCircle.getRadius() * currentCircle.getRadius();
initializeForNewCircle(circle);
}
initializeForNewCircle是抽象的,其中一种实现方式是将圆的半径存储起来,以避免进行平方根运算。现在回到processCircleShape。在调用initializeForNewCirclePrivate后,我们检查多边形是否为null(我理解为空多边形),如果是null,则返回。在这种情况下,计算出的面积将为零。如果多边形不为null,则我们获取多边形的PathIterator。我调用getPathIterator方法的参数是可以应用于路径的仿射变换。但我不想应用它,所以我只是传递了null。
接下来,我声明将跟踪顶点的double[],必须记住第一个顶点,因为PathIterator仅向我提供每个顶点一次,所以在它给出最后一个顶点后,我必须返回并形成与此最后一个顶点和第一个顶点连通的边缘。
下一行的currentSegment方法将下一个顶点放入其参数中。它返回一个代码,告诉您何时已经没有顶点了。这就是为什么我的while循环的控制表达式是它的原因。
该方法的大部分其余代码都是与迭代顶点相关的无趣逻辑。重要的是,在每次while循环迭代中,我调用processSegment,然后在方法末尾再次调用processSegment以处理连接最后一个顶点和第一个顶点的边缘。
让我们看一下processSegment的代码:
private void processSegment(double[] initialVertex, double[] finalVertex) {
double[] segmentDisplacement = displacment2D(initialVertex, finalVertex);
if (segmentDisplacement[0] == 0 && segmentDisplacement[1] == 0) {
return;
}
double segmentLength = Math.sqrt(dotProduct2D(segmentDisplacement, segmentDisplacement));
double[] centerToInitialDisplacement = new double[]{initialVertex[0] - getCurrentCircle().getCenterX(), initialVertex[1] - getCurrentCircle().getCenterY()};
final double leftX = dotProduct2D(centerToInitialDisplacement, segmentDisplacement) / segmentLength;
final double rightX = leftX + segmentLength;
final double y = wedgeProduct2D(segmentDisplacement, centerToInitialDisplacement) / segmentLength;
processSegmentStandardGeometry(leftX, rightX, y);
}
在这个方法中,我实现了将边缘转换为上述标准几何形状的步骤。首先,我计算segmentDisplacement,即从初始顶点到最终顶点的位移。这定义了标准几何形状的x轴。如果这个位移为零,我会提前返回。
接下来,我计算位移的长度,因为这对于获取x单位向量是必要的。一旦我有了这个信息,我就计算了从圆的中心到初始顶点的位移。这个位移与segmentDisplacement的点积给出了我之前称为xi的leftX。然后,我计算rightX,即xf,只需leftX + segmentLength。最后,我执行楔积以获取如上所述的y。
现在,我已经将问题转换为标准几何形状,处理起来将变得容易。这就是processSegmentStandardGeometry方法所做的事情。让我们看看代码。
private void processSegmentStandardGeometry(double leftX, double rightX, double y) {
if (y * y > getCurrentSquareRadius()) {
processNonIntersectingRegion(leftX, rightX, y);
} else {
final double intersectionX = Math.sqrt(getCurrentSquareRadius() - y * y);
if (leftX < -intersectionX) {
final double leftRegionRightEndpoint = Math.min(-intersectionX, rightX);
processNonIntersectingRegion(leftX, leftRegionRightEndpoint, y);
}
if (intersectionX < rightX) {
final double rightRegionLeftEndpoint = Math.max(intersectionX, leftX);
processNonIntersectingRegion(rightRegionLeftEndpoint, rightX, y);
}
final double middleRegionLeftEndpoint = Math.max(-intersectionX, leftX);
final double middleRegionRightEndpoint = Math.min(intersectionX, rightX);
final double middleRegionLength = Math.max(middleRegionRightEndpoint - middleRegionLeftEndpoint, 0);
processIntersectingRegion(middleRegionLength, y);
}
}
第一个if区分了y足够小以至于边缘可能与圆相交的情况。如果y很大且没有可能相交,则调用处理该情况的方法。否则,我处理可能相交的情况。
如果可能相交,我计算相交的x坐标intersectionX,并将边缘分成三个部分,对应于上面标准几何图形的1、2和3区域。首先我处理区域1。
为了处理区域1,我检查leftX是否确实小于-intersectionX,否则就没有区域1。如果有区域1,则需要知道它何时结束。它在rightX和-intersectionX的最小值处结束。找到这些x坐标后,我处理这个非交叉区域。
我做类似的事情来处理区域3。
对于区域2,我需要进行一些逻辑检查,以确保
leftX和
rightX实际上将某个区域括在
-intersectionX和
intersectionX之间。找到该区域后,我只需要该区域的长度和
y,因此我将这两个数字传递给一个处理区域2的抽象方法。
现在让我们看一下
processNonIntersectingRegion的代码。
private void processNonIntersectingRegion(double leftX, double rightX, double y) {
final double initialTheta = Math.atan2(y, leftX);
final double finalTheta = Math.atan2(y, rightX);
double deltaTheta = finalTheta - initialTheta;
if (deltaTheta < -Math.PI) {
deltaTheta += 2 * Math.PI;
} else if (deltaTheta > Math.PI) {
deltaTheta -= 2 * Math.PI;
}
processNonIntersectingRegion(deltaTheta);
}
我只是使用atan2来计算leftX和rightX之间的角度差。然后我添加了处理atan2不连续性的代码,但这可能是不必要的,因为不连续性发生在180度或0度。然后我将角度差传递给一个抽象方法。最后我们只有抽象方法和获取器:
protected abstract void initialize();
protected abstract void initializeForNewCircle(Circle circle);
protected abstract void processNonIntersectingRegion(double deltaTheta);
protected abstract void processIntersectingRegion(double length, double y);
protected abstract T getValue();
protected final Circle getCurrentCircle() {
return currentCircle;
}
protected final double getCurrentSquareRadius() {
return currentSquareRadius;
}
}
现在让我们来看看扩展类
CircleAreaFinder。
public class CircleAreaFinder extends CircleShapeIntersectionFinder<Double> {
public static double findAreaOfCircle(Circle circle, Shape shape) {
CircleAreaFinder circleAreaFinder = new CircleAreaFinder();
return circleAreaFinder.computeValue(circle, shape);
}
double area;
@Override
protected void initialize() {
area = 0;
}
@Override
protected void processNonIntersectingRegion(double deltaTheta) {
area += getCurrentSquareRadius() * deltaTheta / 2;
}
@Override
protected void processIntersectingRegion(double length, double y) {
area -= length * y / 2;
}
@Override
protected Double getValue() {
return area;
}
@Override
protected void initializeForNewCircle(Circle circle) {
}
}
它有一个字段
area 来跟踪区域。如预期,
initialize 将区域设置为零。当我们处理不相交的边缘时,我们按照上面得出的结论,将区域增加R ^ 2Δθ / 2。对于相交的边缘,我们减少了
y * length / 2 区域。这是为了使
y 的负值对应于正面积,因为我们决定它们应该这样做。
现在很好的一件事是,如果我们想跟踪周长,我们不必做太多的工作。我定义了一个 AreaPerimeter 类:
public class AreaPerimeter {
final double area;
final double perimeter;
public AreaPerimeter(double area, double perimeter) {
this.area = area;
this.perimeter = perimeter;
}
public double getArea() {
return area;
}
public double getPerimeter() {
return perimeter;
}
}
现在我们只需要再次扩展我们的抽象类,使用AreaPerimeter作为类型即可。
public class CircleAreaPerimeterFinder extends CircleShapeIntersectionFinder<AreaPerimeter> {
public static AreaPerimeter findAreaPerimeterOfCircle(Circle circle, Shape shape) {
CircleAreaPerimeterFinder circleAreaPerimeterFinder = new CircleAreaPerimeterFinder();
return circleAreaPerimeterFinder.computeValue(circle, shape);
}
double perimeter;
double radius;
CircleAreaFinder circleAreaFinder;
@Override
protected void initialize() {
perimeter = 0;
circleAreaFinder = new CircleAreaFinder();
}
@Override
protected void initializeForNewCircle(Circle circle) {
radius = Math.sqrt(getCurrentSquareRadius());
}
@Override
protected void processNonIntersectingRegion(double deltaTheta) {
perimeter += deltaTheta * radius;
circleAreaFinder.processNonIntersectingRegion(deltaTheta);
}
@Override
protected void processIntersectingRegion(double length, double y) {
perimeter += Math.abs(length);
circleAreaFinder.processIntersectingRegion(length, y);
}
@Override
protected AreaPerimeter getValue() {
return new AreaPerimeter(circleAreaFinder.getValue(), perimeter);
}
}
我们有一个变量
perimeter来跟踪周长,我们记住
radius的值以避免频繁调用
Math.sqrt,并将面积计算委托给我们的
CircleAreaFinder。我们可以看到周长的公式很容易。
供参考,这是
CircleShapeIntersectionFinder的完整代码。
private static double[] displacment2D(final double[] initialPoint, final double[] finalPoint) {
return new double[]{finalPoint[0] - initialPoint[0], finalPoint[1] - initialPoint[1]};
}
private static double wedgeProduct2D(final double[] firstFactor, final double[] secondFactor) {
return firstFactor[0] * secondFactor[1] - firstFactor[1] * secondFactor[0];
}
static private double dotProduct2D(final double[] firstFactor, final double[] secondFactor) {
return firstFactor[0] * secondFactor[0] + firstFactor[1] * secondFactor[1];
}
private Circle currentCircle;
private double currentSquareRadius;
public final T computeValue(Circle circle, Shape shape) {
initialize();
processCircleShape(circle, shape);
return getValue();
}
private void processCircleShape(Circle circle, final Shape cellBoundaryPolygon) {
initializeForNewCirclePrivate(circle);
if (cellBoundaryPolygon == null) {
return;
}
PathIterator boundaryPathIterator = cellBoundaryPolygon.getPathIterator(null);
double[] firstVertex = new double[2];
double[] oldVertex = new double[2];
double[] newVertex = new double[2];
int segmentType = boundaryPathIterator.currentSegment(firstVertex);
if (segmentType != PathIterator.SEG_MOVETO) {
throw new AssertionError();
}
System.arraycopy(firstVertex, 0, newVertex, 0, 2);
boundaryPathIterator.next();
System.arraycopy(newVertex, 0, oldVertex, 0, 2);
segmentType = boundaryPathIterator.currentSegment(newVertex);
while (segmentType != PathIterator.SEG_CLOSE) {
processSegment(oldVertex, newVertex);
boundaryPathIterator.next();
System.arraycopy(newVertex, 0, oldVertex, 0, 2);
segmentType = boundaryPathIterator.currentSegment(newVertex);
}
processSegment(newVertex, firstVertex);
}
private void initializeForNewCirclePrivate(Circle circle) {
currentCircle = circle;
currentSquareRadius = currentCircle.getRadius() * currentCircle.getRadius();
initializeForNewCircle(circle);
}
private void processSegment(double[] initialVertex, double[] finalVertex) {
double[] segmentDisplacement = displacment2D(initialVertex, finalVertex);
if (segmentDisplacement[0] == 0 && segmentDisplacement[1] == 0) {
return;
}
double segmentLength = Math.sqrt(dotProduct2D(segmentDisplacement, segmentDisplacement));
double[] centerToInitialDisplacement = new double[]{initialVertex[0] - getCurrentCircle().getCenterX(), initialVertex[1] - getCurrentCircle().getCenterY()};
final double leftX = dotProduct2D(centerToInitialDisplacement, segmentDisplacement) / segmentLength;
final double rightX = leftX + segmentLength;
final double y = wedgeProduct2D(segmentDisplacement, centerToInitialDisplacement) / segmentLength;
processSegmentStandardGeometry(leftX, rightX, y);
}
private void processSegmentStandardGeometry(double leftX, double rightX, double y) {
if (y * y > getCurrentSquareRadius()) {
processNonIntersectingRegion(leftX, rightX, y);
} else {
final double intersectionX = Math.sqrt(getCurrentSquareRadius() - y * y);
if (leftX < -intersectionX) {
final double leftRegionRightEndpoint = Math.min(-intersectionX, rightX);
processNonIntersectingRegion(leftX, leftRegionRightEndpoint, y);
}
if (intersectionX < rightX) {
final double rightRegionLeftEndpoint = Math.max(intersectionX, leftX);
processNonIntersectingRegion(rightRegionLeftEndpoint, rightX, y);
}
final double middleRegionLeftEndpoint = Math.max(-intersectionX, leftX);
final double middleRegionRightEndpoint = Math.min(intersectionX, rightX);
final double middleRegionLength = Math.max(middleRegionRightEndpoint - middleRegionLeftEndpoint, 0);
processIntersectingRegion(middleRegionLength, y);
}
}
private void processNonIntersectingRegion(double leftX, double rightX, double y) {
final double initialTheta = Math.atan2(y, leftX);
final double finalTheta = Math.atan2(y, rightX);
double deltaTheta = finalTheta - initialTheta;
if (deltaTheta < -Math.PI) {
deltaTheta += 2 * Math.PI;
} else if (deltaTheta > Math.PI) {
deltaTheta -= 2 * Math.PI;
}
processNonIntersectingRegion(deltaTheta);
}
protected abstract void initialize();
protected abstract void initializeForNewCircle(Circle circle);
protected abstract void processNonIntersectingRegion(double deltaTheta);
protected abstract void processIntersectingRegion(double length, double y);
protected abstract T getValue();
protected final Circle getCurrentCircle() {
return currentCircle;
}
protected final double getCurrentSquareRadius() {
return currentSquareRadius;
}
总之,这就是我的算法描述。我认为它很好,因为它非常精确,而且需要检查的情况并不是很多。






 第二个区域看起来会像这样
第二个区域看起来会像这样
 第三个区域将是
第三个区域将是
 同样,在我们的情况下,前两个区域是正的,而第三个区域将是负的。希望取消将起作用,以便净面积确实是我们感兴趣的面积。让我们看看。
同样,在我们的情况下,前两个区域是正的,而第三个区域将是负的。希望取消将起作用,以便净面积确实是我们感兴趣的面积。让我们看看。