如何在三维空间中找到凸壳

Question

给定一组点 S (x, y, z)，如何找到这些点的 凸包(convex hull) ?

我试图理解来自这里的算法，但没有得到太多信息。

它说：

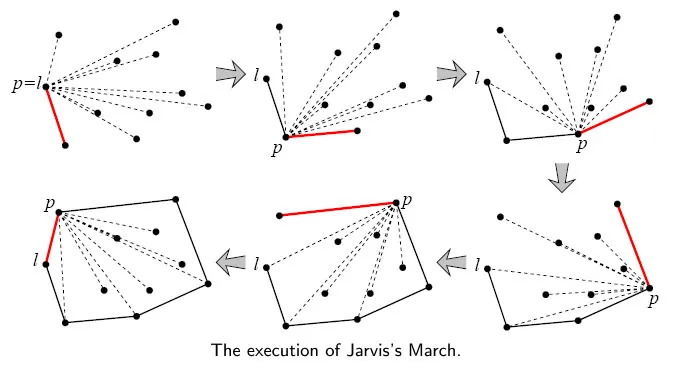
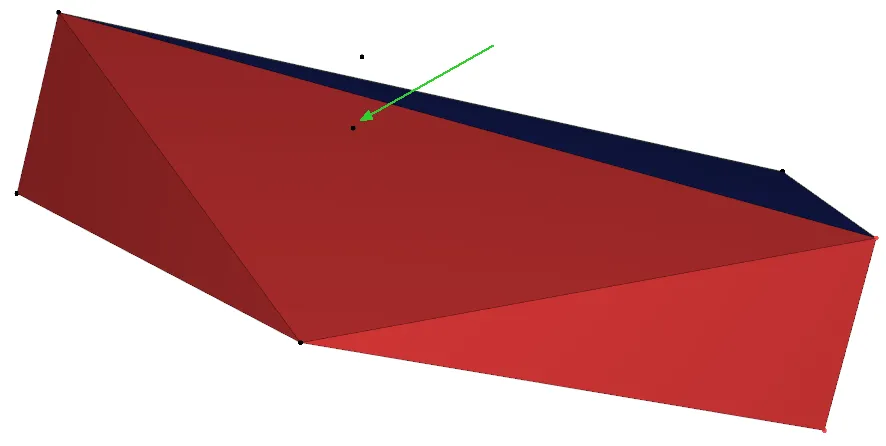
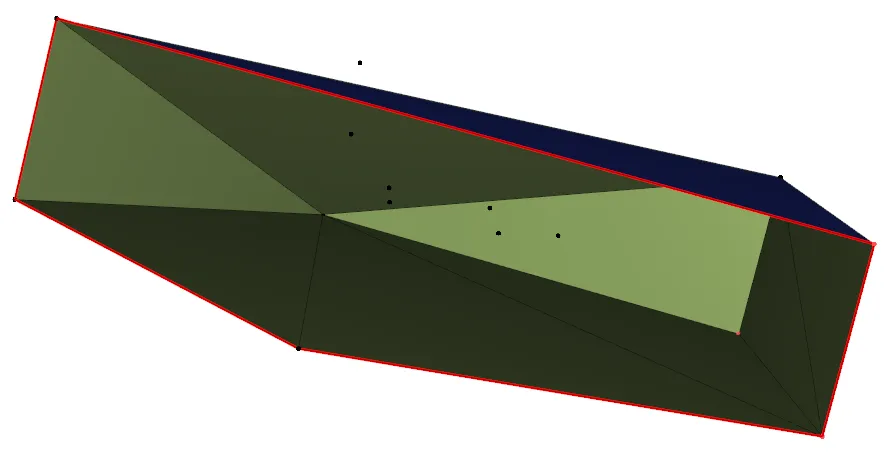
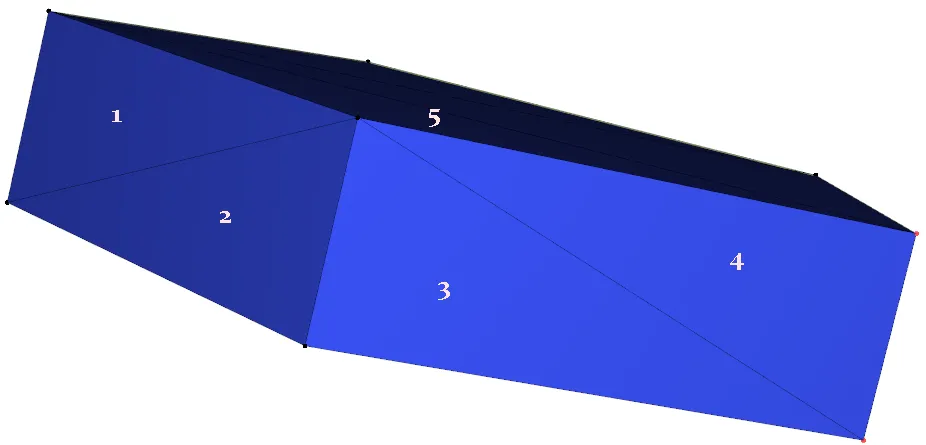
首先将所有点投影到xy平面上，并通过选择具有最高y坐标的点并执行一次礼品包装(gift wrapping)来确定边缘上的另一个端点，从而找出肯定在凸壳上的边缘。这是不完整凸壳的第一部分。然后我们逐步构建外壳。考虑这个第一条边;现在找到另一个点以形成外壳的第一个三角形面。我们通过选择这个点来完成此操作，使得当适当地查看时，所有其他点都位于该三角形面的右侧(就像在礼品包装算法中那样，我们选择了一条边，使得所有其他点都在该边的右侧)。现在有三条边在凸壳中；继续进行，我们随意选择其中之一，再次浏览所有点以找到另一个点以该边建立新的三角形面，重复此过程，直到没有剩余的边。(当我们创建一个新的三角形面时，我们会向池中添加两条边；但是，我们必须首先检查它们是否已经被添加到凸壳中，在这种情况下，我们会忽略它们。)面数为O(n)，每次迭代需要O(n)的时间，因为我们必须扫描所有剩余的点，总共的时间复杂度为O(n2)。

请问有没有人能以更清晰的方式解释它或提出一个更简单的替代方法？

- Ninja420

Answer 1

实现3D凸包不容易，但已经有许多算法被实现了，并且代码已经广泛可用。在质量和使用时间的高端是CGAL。在这两个方面的低端是我自己的C代码:
     
在这之间，网上有大量代码可用，包括这个QuickHull的实现。

- Joseph O'Rourke

---

这个 QuickHull 实现的网站似乎已经消失了。在这里可以找到存档：https://web.archive.org/web/20180106161310/http://thomasdiewald.com/blog/?p=1888 - Alec Jacobson

很抱歉，这只是一个链接答案。 - Fedor

很抱歉，这只是一个链接回答，没有提供具体的内容。 - undefined

Answer 2

我建议首先尝试一个更简单的方法，比如快速外壳算法。(顺便说一句，gift wrapping的时间复杂度是O(nh)而不是O(n²)，其中h是凸包上的点数，快速外壳的时间复杂度为O(n log n))。

在一般情况下，快速外壳算法表现相当不错，但在高对称性或点位于圆周上时，处理通常会变慢。快速外壳算法可以分解为以下步骤：

1. 找到x坐标最小和最大的点，这些点必定是凸包的一部分。

2. 使用由两个点形成的直线将集合分成两个子集合，这些子集合将递归处理。

3. 确定在直线的一侧距离最远的点。找到之前发现的两个点以及这个点，它们组成一个三角形。

4. 在该三角形内部的点不能成为凸包的一部分，因此可以在下一步中忽略掉。

5. 在三角形形成的两条直线上重复前面的两个步骤（不是最初的直线）。

6. 重复上述步骤，直到没有更多的点，递归已经结束，所选的点构成凸包。

请查看这个使用快速外壳算法实现和解释三维凸包的例子。

gift wrapping算法：

Jarvis 的匹配算法就像把一根绳子缠绕在点上。它首先计算最左边的点 l，因为我们知道最左边的点必须是凸包的一个顶点。这个过程需要线性时间。然后算法通过一系列的枢轴步骤来找到每一个连续的凸包顶点，直到下一个顶点又是最初的最左边的点。

算法如下寻找连续的凸包顶点：紧随点 p 后的顶点是那些看起来最靠右的点，当站在点 p 上并看向其他点时。换句话说，如果 q 是紧随 p 的顶点，而 r 是任何其他输入点，则三元组 p、q、r 是逆时针顺序的。通过执行一系列的 O(n) 逆时针测试，我们可以在线性时间内找到每个连续的顶点。

由于算法对于每一个凸包顶点都花费了 O(n) 的时间，所以最坏情况下的运行时间是 O(n2)。然而，如果凸包只有很少的顶点，Jarvis's march 就会非常快。更好的表达运行时间的方式是 O(nh)，其中 h 是凸包顶点的数量。在最坏情况下，h = n，我们获得了旧的 O(n2) 时间界限，但在最好的情况下，h = 3，算法只需要 O(n) 的时间。这是一种所谓的输出敏感算法，输出越小，算法速度越快。

以下图片应该能够更好地说明这个过程：

- Aditya

---

似乎 OP 正在寻求 3D 船体方面的帮助，但是您（很好！）提供的描述是关于 2D 船体的…… - Joseph O'Rourke

如果你理解2D，那么3D就是一个非常简单的概括。 ;) - Aditya

我实际操作过这两种方法，我认为它们在不同的方面都有各自的优劣。 :) - Joseph O'Rourke

Answer 3

寻找三维凸包的GPL C++代码可以在http://www.newtonapples.net/code/NewtonAppleWrapper_11Feb2016.tar.gz找到，并且这个O(n log(n))算法的描述可以在http://www.newtonapples.net/NewtonAppleWrapper.html中找到。

- David

Answer 4

计算三维凸包的最简单算法之一是由Barber等人于1995年在Convex Hulls的QuickHull算法中提出。不幸的是，原始论文缺少任何图示以简化理解。

该算法通过存储一些具有来自原始点集子集的顶点的凸集的边界面来迭代工作。剩余的点被分为已经在当前凸集内部和在外部的点。每个步骤都包括将一个在外面的点包含在内，以扩大凸集，直到没有剩余的点为止。

作者建议从任意四个原始点构成的四面体中开始进行三维算法。如果选择的这些顶点位于凸壳的边界上，则可以加速算法（它们在以下步骤中不会从边界中移除）。此外，该算法还可以从只包含两个方向相反的三角形且有3个原始点的边界表面开始。这些点可以按以下方式选择。

1. 如果按字典顺序比较坐标，第一个点具有最小的(x,y,z)坐标。
2. 第二个点是距离第一个点最远的点。
3. 第三个点是距离通过前两个点的直线最远的点。

下图显示了初始点和起始的两个相反方向的三角形： 其余的点被分成两组：

1. 黑色点 - 在包含三角形的平面上方 - 与法线朝上的三角形相关联。
2. 红色点 - 在包含三角形的平面下方 - 与法线朝下的三角形相关联。

在接下来的步骤中，算法总是将当前在凸集外部的每个点与其中一个边界三角形相关联，该三角形从该点“可见”（点位于该三角形的正半空间内）。更准确地说，每个外部点都与一个三角形相关联，该三角形与该点之间的距离最大。

在算法的每个步骤中，选择最远的外部点，然后识别从它可见的当前凸集的所有面，这些面从凸集中移除，并用具有一个顶点在最远点和另外两个点在“地平线脊”的三角形替换（已移除可见面的边界）。

在下图中，最远点由绿色箭头指示，三个可见三角形用红色突出显示： 可见三角形被删除，背面和内部点可以在孔中看到，地平线脊以红色显示： 5个新三角形（在添加点处连接）修补了表面上的孔：

之前与被移除的三角形相关联的点，要么成为更新后凸集的内部点，要么在新的三角形之间重新分配。

最后一张图展示了凸包计算的最终结果，没有任何剩余的外部点。（这些图是在MeshInspector应用程序中准备的，该应用程序实现了此算法。）

- Fedor