Faulhaber公式的高效实现

Question

我希望得到一个高效的Faulhaber's Formula实现。

我的答案是

F(N,K) % P

其中F(N,K)是Faulhaber's formula的实现，P是一个质数。

注意：N非常大，最多达到10^16，K最大为3000

我尝试了给定网站上的双重级数实现。 但对于非常大的n和k来说，这需要太多时间。 有人可以帮助使此实现更加有效或描述其他实现该公式的方法吗？

- coder hacker

---

这是来自欧拉项目吗？我怀疑你需要更深入地利用计算模P的事实。 - David Eisenstat

是的，我考虑过，但伯努利数是分数，所以很难利用。但我不知道... - coder hacker

我认为之前有人在这里评论过，这个问题可能来自于这里：https://www.hackerrank.com/contests/infinitum-mar14/challenges/summing-the-k-n-series。在那里，K最大可达10^3（1000），P = 10^9 + 7。 - גלעד ברקן

我想我成功了。请查看我的更新答案。 - גלעד ברקן

Answer 1

您觉得使用 Schultz（1980）的想法如何？在您提到的双级数实现（mathworld.wolfram.com/PowerSum.html）下面进行了概述。

来自 Wolfram MathWorld：

    Schultz（1980）表明，可以通过编写式子 S_p(n) 来找到总和。

    

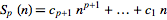
并解决p+1个方程组

    

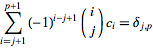
对于j=0,1,...,p (Guo和Qi 1999)获得，其中delta (j,p)是Kronecker delta。

下面是一个在Haskell中尝试的例子，似乎可以正常工作。 在我的旧笔记本电脑上，n = 10 ^ 16，p = 1000的结果大约在36秒内返回。

{-# OPTIONS_GHC -O2 #-}

import Math.Combinatorics.Exact.Binomial
import Data.Ratio
import Data.List (foldl')

kroneckerDelta a b | a == b    = 1 % 1
                   | otherwise = 0 % 1

g a b = ((-1)^(a - b +1) * choose a b) % 1

coefficients :: Integral a => a -> a -> [Ratio a] -> [Ratio a]
coefficients p j cs
  | j < 0     = cs
  | otherwise = coefficients p (j - 1) (c:cs)
 where
   c = f / g (j + 1) j
   f = foldl h (kroneckerDelta j p) (zip [j + 2..p + 1] cs)
   h accum (i,cf) = accum - g i j * cf

trim r = let n = numerator r
             d = denominator r
             l = div n d
         in (mod l (10^9 + 7),(n - d * l) % d)

s n p = numerator (a % 1 + b) where
 (a,b) = foldl' (\(i',r') (i,r) -> (mod (i' + i) (10^9 + 7),r' + r)) (0,0) 
      (zipWith (\c i ->  trim (c * n^i)) (coefficients p p []) [1..p + 1])

main = print (s (10^16) 1000)

- גלעד ברקן

Answer 2

我发现了一种自己的算法来计算从Faulhaber公式得出的多项式的系数；它、它的证明以及几个实现可以在 github.com/fcard/PolySum 找到。这个问题激发了我加入一个C++实现（使用GMP库进行任意精度数字运算），截至撰写本文时，除了一些可用性特征之外：

#include <gmpxx.h>
#include <vector>

namespace polysum {
  typedef std::vector<mpq_class> mpq_row;
  typedef std::vector<mpq_class> mpq_column;
  typedef std::vector<mpq_row>   mpq_matrix;

  mpq_matrix make_matrix(size_t n) {
    mpq_matrix A(n+1, mpq_row(n+2, 0));
    A[0] = mpq_row(n+2, 1);

    for (size_t i = 1; i < n+1; i++) {
      for (size_t j = i; j < n+1; j++) {
        A[i][j] += A[i-1][j];
        A[i][j] *= (j - i + 2);
      }
      A[i][n+1] = A[i][n-1];
    }
    A[n][n+1] = A[n-1][n+1];
    return A;
  }

  void reduced_row_echelon(mpq_matrix& A) {
    size_t n = A.size() - 1;
    for (size_t i = n; i+1 > 0; i--) {
      A[i][n+1] /= A[i][i];
      A[i][i] = 1;
      for (size_t j = i-1; j+1 > 0; j--) {
        auto p = A[j][i];
        A[j][i] = 0;
        A[j][n+1] -= A[i][n+1] * p;
      }
    }
  }

  mpq_column sum_coefficients(size_t n) {
    auto A = make_matrix(n);
    reduced_row_echelon(A);

    mpq_column result;
    for (auto row: A) {
      result.push_back(row[n+1]);
    }
    return result;
  }
}

我们可以这样使用上面的代码：

#include <cmath>
#include <gmpxx.h>
#include <polysum.h>

mpq_class power_sum(size_t K, unsigned int N) {
  auto coeffs = polysum::sum_coefficients(K)

  mpq_class result(0);
  for (size_t i = 0; i <= K; i++) {
    result += A[i][n+1] * pow(N, i+1);
  }
  return result;
}

完整的实现提供了一个可打印和可调用的Polynomial类，以及一个polysum函数，用于将一个多项式构造为另一个多项式的总和。

#include "polysum.h"

void power_sum_print(size_t K, unsigned int N) {
  auto F = polysum::polysum(K);
  std::cout << "polynomial: " << F;
  std::cout << "result: " << F(N);
}

就效率而言，上述代码在我的电脑上计算出K=1000和N=1e16的结果只需约1.75秒，相比之下，更成熟和优化的SymPy实现在同一台机器上需要约90秒，而Mathematica则需要30秒。对于K=3000，上述代码需要约4分钟，Mathematica几乎需要20分钟（但使用的内存较少），而我让SymPy运行了整整一晚上，但它没有完成，可能是因为它用完了内存。

在这里可以进行的优化包括使矩阵稀疏化，并利用只有一半的行和列需要计算的事实。链接存储库中的Rust版本实现了稀疏和行优化，计算K=1000大约需要0.7秒，计算K=3000大约需要45秒（分别使用105mb和2.9gb内存）。Haskell版本实现了所有三个优化，计算K=1000大约需要1秒，计算K=3000大约需要34秒（分别使用60mb和880mb内存），而完全未经优化的Python实现计算K=1000大约需要12秒，但计算K=3000时会耗尽内存。

看起来这个方法是最快的，无论使用什么语言，但研究还在进行中。由于Schultz的方法归结为解决一个n+1方程组，应该能够以同样的方式进行优化，这将取决于他的矩阵是否更快地计算。此外，内存使用不断增加，Mathematica仍然是明显的赢家，在K=3000时仅使用80mb。我们拭目以待。

- phicr

Answer 3

我用一个简单的Julia脚本构建了一个公式，这个公式是 Faulhaber错过的（就像他错过的他所研究的其他20,000个公式一样，真是可耻）。

function faulhaber(d)
    polyVector = [big(0)//big(1) for n = 1:d+2]
    #initialisation at d = 1, indices shifted by 1!
    polyVector[2] = 1/2
    polyVector[3] = 1/2
    for j=2:d
        oldUnit = polyIntEval(polyVector, 1)
        for k=j+2:-1:3
            polyVector[k] = j * polyVector[k-1]/(k-1)
        end
        polyVector[2] = 1 - j*oldUnit
    end
    return polyVector
end

function polyIntEval(v, x)
    d = length(v) - 1
    result = 0
    for j=0:d
        result += v[j+1]*x^(j+1) / (j+1)
    end
    return result
end

在我的笔记本电脑上，获取 d = 1000 的完整多项式大约需要5秒钟。

- AlgebraicsAnonymous

---

d = 3000大约需要半分钟的时间。所以很可能这确实比其他方法更优越。 - undefined