寻找同构排列集的算法

Question

寻找同构排列集的算法

c++carraysalgorithmpermutation

16

我有一个由排列集合组成的数组，想要移除同构排列。

我们有S个排列集合，每个集合包含K个排列，每个排列由N个元素组成。目前我将它保存为一个数组int pset[S][K][N]，其中S、K和N是固定的，N大于K。

如果存在一个置换P，可以将A中的元素转换为B中的元素（例如，如果a是集合A中的元素，则P(a)是集合B中的元素），则称两个排列集合A和B同构。在这种情况下，我们可以说P使A和B同构。

我的当前算法是：

1. 我们选择所有满足i < j的对s1 = pset[i]和s2 = pset[j]。 2. 从所选集合（s1和s2）中的每个元素都被编号为1到K。这意味着每个元素可以表示为s1[i]或s2[i]，其中0 < i < K+1。 3. 对于每个K元素的排列T，我们执行以下操作： - 找到置换R，使得R(s1[1]) = s2[1]。 - 检查R是否是一种使s1和T(s2)同构的排列，其中T(s2)是集合s2的元素（排列）的重新排列，因此我们只需检查R(s1[i]) = s2[T[i]]，其中0 < i < K+1。 - 如果不是，则我们继续下一个排列T。

这个算法运行速度非常慢：第一步的时间复杂度是O(S^2)，每次循环检查排列T所需时间复杂度为O(K!)，寻找R所需的时间复杂度是O(N^2)，检查R是否与使s1和s2同构的排列匹配所需的时间复杂度为O(K*N) - 因此总时间复杂度是O(S^2 * K! * N^2)。

问题：我们能使它更快吗？

- Chan Kha Vu

1

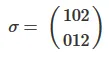
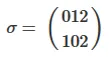
我认为你可以将 K! 乘法器改进为多项式：对于每一个 i 和 j，找到置换 R 使得 R(s1[i]) = s2[j]，标记 j 为 "used"，然后对于每个 k != i，找到一个未被标记的 m，使得 R(s1[k]) = s2[m]，并标记 m 为 "used"。如果对于某些 i 和 j，您可以 "标记" 所有从 1 到 K 的 m，那么 R 会使 s1 和 s2 同构。 - Kolmar

这必须有多稳定？您可以将它们全部排序，O（n * m lgm），其中n是序列数，m是序列长度。然后您可以将它们全部添加到一个集合中，如果比较为O（m），则会为O（n * lg（n）* m），从而使总成本为O（n * m * lg（n）））。 - IdeaHat

@frenk 我认为这个函数是由一个置换引起的，即Pa被定义为一个由p和a组成的置换。 - vsoftco

1

你的映射是如何定义的？是在置换的左乘下，A\isomorphic B？还是在共轭下，即 B = p A inverse(p)？ - vsoftco

@frenk 排列是一种函数，但并非每个函数都是排列。 {123、111、321} 和 {321、333、123} 这种情况不适用于我的问题，因为 111 和 333 都不是排列。 - Chan Kha Vu

显示剩余3条评论

5个回答

5

这个问题有一个非常简单的解决方案：转置。

如果两个集合是同构的，意味着存在一种一对一的映射，其中在集合S1中索引为i的所有数字的集合等于在集合S2中某个索引k处的所有数字的集合。我的猜想是，没有两个非同构的集合具有此属性。

(1) Jean Logeart的例子：

0: [[1,2,3],[3,2,1]]
1: [[2,3,1],[1,3,2]]
2: [[1,2,3],[2,3,1]]
3: [[3,2,1],[1,2,3]]

Perform ONE pass:

Transpose, O(n):
0: [[1,3],[2,2],[3,1]]

Sort both in and between groups, O(something log something):
0: [[1,3],[1,3],[2,2]]

Hash:
"131322" -> 0

...
"121233" -> 1
"121323" -> 2
"131322" -> already hashed.

0 and 3 are isomorphic.

(2) vsoftco在他对Jean Logeart答案的评论中提供了一个反例:

A = [ [0, 1, 2], [2, 0, 1] ]
B = [ [1, 0, 2], [0, 2, 1] ]

"010212" -> A
"010212" -> already hashed.

A and B are isomorphic.

你可以将每个集合转换为转置排序字符串或哈希表或任何压缩对象，以进行线性比较。请注意，该算法将所有三个集合A、B和C视为同构，即使一个p将A转换为B，另一个p将A转换为C也是如此。显然，在这种情况下，有p将这三个集合中的任何一个转换为另一个，因为我们所做的就是将一个集合中的每个i移动到另一个集合中的特定k。如果，正如你所说，你的目标是“删除同构排列”，你仍将得到要删除的一组列表。

解释：

假设除了我们的排序哈希之外，我们还记录了每个i来自哪个排列。vsoftco的反例：

010212  // hash for A and B
100110  // origin permutation, set A
100110  // origin permutation, set B

为了确认同构，我们需要展示第一个集合中每个索引处分组的 i 移动到第二个集合的某个索引处，索引不重要。对 i 进行分组排序不会使解决方案无效，相反它有助于确认集合之间的移动/排列。

现在，根据定义，哈希表中每个组中的每个数字都代表了原始排列中的一个集合，并且对于每个集合，每个数字在哈希表中仅表示一次。无论我们选择如何排列哈希表中每个组中的数字，我们都可以保证该组中的每个数字都代表着集合中不同的排列；并且一旦我们理论上分配了该数字，我们就可以保证它仅被保留用于该排列和索引。对于给定的数字，例如2，在两个哈希表中，我们可以保证它来自于集合A中的一个索引和排列，在第二个哈希表中对应于集合B中的一个索引和排列。这就是我们需要展示的全部内容 - 在一个集合（由不同的组成）中，每个排列中的一个索引只去了另一个集合（由不同的组成）中的一个索引。数字属于哪个排列和索引是不相关的。

记住，任何与集合S1同构的集合S2，都可以通过对S1的成员应用一个排列函数或不同排列函数的各种组合来推导出。我们实际上所表示的排序或重新排序的数字和组的含义是我们选择分配作为同构解决方案的置换，而不是哪个数字来自哪个索引和置换的实际分配。这里是vsoftco的反例，这次我们将添加哈希的原始索引：

110022 // origin index set A
001122 // origin index set B

因此，我们的排列，作为同构的解决方案，是：

enter image description here

或者，按顺序：

enter image description here

（请注意，在Jean Logeart的示例中，同构存在多个解决方案。）

- גלעד ברקן

你的算法似乎是有效的，我只是想理解一下为什么 :) 你有在其他更多排列组合的示例上进行测试吗？ - vsoftco

根据FalconUA的定义，“同构”意味着一个置换函数将集合A的所有置换映射到集合B的所有置换（它们都包含K个置换）。这意味着，A中每个索引i的置换将会对应到B中特定的索引k的置换（例如，所有的S[A][1]将会对应到S[B][5]）。我们只需要检查A和B中按索引分组的置换是否包含相同的数字。一种简单的方法是对这些分组进行排序。 - גלעד ברקן

1

为了确保我们使用相同的约定... [3,2,0,1] \composed [1,2,0,3] = [2,0,3,1]，对吗？你可以从最右边的排列开始，0->1->2, 1->2->0, 2->0->3, 3->3->1。 - vsoftco

1

@vsoftco 不太确定我理解你的意思。我的做法是将置换 [3,2,0,1] 应用于 [1,2,0,3] 和 [3,1,0,2] 中的每一个：对于第一个，[1,2,0,3]：1 去到索引 3；2 去到索引 2；0 去到索引 0；3 去到索引 1。明白了吗？ - גלעד ברקן

1

@גלעדברקן 我认为你的组合是反向的 http://math.stackexchange.com/questions/549186/the-product-or-composition-of-permutation-groups-in-two-line-notation - vsoftco

显示剩余7条评论

4

在集合A中选择a0，找到它的逆（快速，O(N)），称其为a0inv。然后在集合B中选择一些i，并定义Pi = bi * ainv，当a在A上变化时，检查Pi * a是否生成B。对于B中的每个i都这样做。如果没有找到任何满足关系的i，则集合不同构。如果找到这样的i，则集合同构。每对集合的运行时间是O(K^2)，需要检查O(S^2)对集合，因此最终复杂度为O(S^2 * K^2 * N)。

注：我在此假设“将A映射到B”是指在排列组合下的映射，因此P(a)实际上是由排列P和排列a组合得到的结果，并且我使用了一个事实，即如果P是一个排列，则必须存在一个i，使得Pa = bi，其中bi是B中的某个元素。

编辑：我决定取消删除我的答案，因为我不确定基于搜索的先前答案（@Jean Logeart）是否正确。如果是的话，我很乐意删除我的答案，因为它效率较低，但我认为我有一个反例，请参见Jean答案下面的评论。

- vsoftco

是的，我认为你对Jean Logeart的回答的反例是正确的。请看我的回答。 - גלעד ברקן

4

假设S中的两个元素s1, s2是同构的。那么，如果p1和p2是置换，则当且仅当pi（si）是应用pi到si中的每个元素所获得的置换集合时，s1同构于s2，其中pi（si）是将pi应用于si的每个元素所得到的置换集合。

对于每个i在1...s和j在1...k中，选择si的第j个成员，并找到将其更改为单位的排列。将它应用于si的所有元素。将k个置换哈希为一个数字，对于任何i和j的选择，在nk的成本下获得k个数字。

比较两个不同的i和j值的哈希集合是k ^ 2 < nk。因此，您可以在s ^ 2 k ^ 3 n的成本下找到候选匹配的集合。如果实际匹配数量很少，则总复杂度远低于您在问题中指定的复杂度。

- Ami Tavory

我认为我找到了一个对数时间的解决方案。 - גלעד ברקן

很酷！你应该把它发布为一个答案。 - Ami Tavory

3

要检查两个集合S₁和S₂是否同构，您可以进行更短的搜索。

如果它们是同构的，则存在一个置换t将S₁的每个元素映射到S₂的元素；要找到t，您只需选择S₁的任何固定元素p并考虑置换。

 t₁ = (1/p) q₁
 t₂ = (1/p) q₂
 t₃ = (1/p) q₃
 ...

对于 S₂ 中的所有元素 q 。因此，如果存在有效的 t ，它必须将元素 p 映射到 S₂ 中的一个元素，因此仅允许将 p 映射到 S₂ 的置换作为可能的候选。

此外，给定一个候选的 t ，要检查两组置换 S₁t 和 S₂ 是否相等，可以使用计算每个元素的哈希码的x-or的哈希值，仅在哈希匹配时才执行所有置换的完整检查。

- 6502

网页内容由stack overflow 提供, 点击上面的

可以查看英文原文，
原文链接

- Jean Logeart · Accepted Answer

您可以进行排序和比较：

// 1 - sort each set of permutation
for i = 0 to S-1
    sort(pset[i])
// 2 - sort the array of permutations itself
sort(pset)
// 3 - compare
for i = 1 to S-1 {
    if(areEqual(pset[i], pset[i-1]))
        // pset[i] and pset[i-1] are isomorphic
}

一个具体的例子：

0: [[1,2,3],[3,2,1]]
1: [[2,3,1],[1,3,2]]
2: [[1,2,3],[2,3,1]]
3: [[3,2,1],[1,2,3]]

第一步：

0: [[1,2,3],[3,2,1]]
1: [[1,3,2],[2,3,1]] // order changed
2: [[1,2,3],[2,3,1]]
3: [[1,2,3],[3,2,1]] // order changed

2秒后：

2: [[1,2,3],[2,3,1]]
0: [[1,2,3],[3,2,1]]
3: [[1,2,3],[3,2,1]] 
1: [[1,3,2],[2,3,1]]

第三步：

(2, 0) not isomorphic 
(0, 3) isomorphic
(3, 1) not isomorphic

复杂度怎么样？

1 是 O(S * (K * N) * log(K * N))
2 是 O(S * K * N * log(S * K * N))
3 是 O(S * K * N)

因此，总体复杂度为 O(S * K * N log(S * K * N))