三角形分割

Question

这是2010年太平洋ACM-ICPC比赛中出现的问题。其重点是尝试找到一种方法，将三角形内一组点分成三个子三角形，使得每个分区恰好包含三分之一的点。

输入：

• 一个边框三角形的坐标：(v1x,v1y),(v2x,v2y),(v3x,v3y)
• 一个数字3n < 30000，代表位于三角形内的点数
• 3n个点的坐标：(x_i,y_i)，其中i=1...3n

输出：

• 一个点(sx,sy)，将三角形分为三个子三角形，使得每个子三角形恰好包含n个点。

分裂点分割边界三角形成子三角形的方式如下：从分裂点向三个顶点绘制一条线。这将把三角形分成3个子三角形。

我们保证这样的点存在。任何这样的点都可以（答案不一定唯一）。

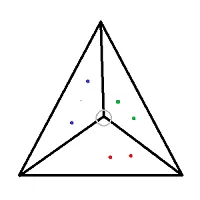
这里是n=2（6个点）问题的示例。我们给出每个彩色点的坐标以及大三角形每个顶点的坐标。分裂点用灰色圆圈标出。

有人能提出比O（n ^ 2）更快的算法吗？

- tskuzzy

---

你应该在这里询问：http://math.stackexchange.com/ - Ariel

这是一个算法问题，而不是数学问题。 - tskuzzy

我想知道质心是否总是一个解。 - Alexey Frunze

我假设你需要一个比O(n^2)更快的算法...问题陈述中的输入边界是什么？ - hugomg

@Alex：不，坐标可以是浮点数。 - tskuzzy

Answer 1

这里有一个O(n log n)的算法。我们假设没有退化。

高级别的思路是，给定一个三角形PQR，

   P
  C \
 /  S\
R-----Q

我们最初将中心点C放在P处。将C滑向R，直到三角形CPQ内有n个点，CQ线段上有一个点S。将C滑向Q，直到三角形CRP不再缺失（扰动C即可完成），或者CP撞到了一个点。在后一种情况下，将C向远离P的方向滑动，直到三角形CRP不再缺失（我们就完成了），或者CQ碰到了一个点，在这种情况下，我们重新开始将C向Q滑动。

显然，实现不能“滑动”点，因此对于涉及C的每个三角形，对于除C之外的该三角形的每个顶点S，将三角形内的点按与S的角度排序存储在二叉查找树中。这些结构足以实现这个动态算法。

我断言此算法是正确的，但未予证明。

至于运行时间，每个事件都是点线交点，可以在O（log n）时间内处理。角度PC、QC和RC都是单调的，所以每条O（1）直线最多只击中每个点一次。

- rom

---

我预见到恶劣的边缘情况，当CP命中多个点而不只是一个时。 - hugomg

@missingno 这就是我在计算几何中默认的退化情况。当存在三个共线点时，通常无法解决这个问题。 - rom

这就是我在编程竞赛中所假设的退化情况，这是标准操作 :) 但现在我已经完全确信了，因为共线情况并没有真正意义上的意义。 - hugomg

@missingo：确实，在原问题中没有考虑共线点的情况。 - tskuzzy

如果CPQ有n个点，当您将C滑向Q时，三角形CPQ在滑动过程中会失去一些点。为什么最终滑动结束后的CPQ三角形仍然包含n个点？ - Antti Huima

Answer 2

主要思路是：如果我们已经得到了一条线，就可以使用线性搜索来找到它上面的一个点。如果这条线不够好，我们可以使用二分搜索来移动它。

具体步骤如下：

1. 根据顶点A与其他点的方向排序，也需要对B和C进行排序。 2. 将顶点A的当前范围设置为所有点。 3. 从顶点A的范围中选择两个中间点。这两个点定义了'A'的子范围。获取某条线段AD，使其位于这些点之间。 4. 遍历从B到AD之间的所有点（从BA开始）。当找到n个点时停止。选择从B到点n以及点n后面（如果没有点在n后面，则使用BC）的方向子范围。如果无法找到少于n个点，则将顶点A的当前范围设置为当前范围的左半部分，并转到步骤3。 5. 对于顶点C，执行与步骤4相同的操作。 6. 如果子范围A、B、C相交，则选择其中任何一点并完成。否则，如果AB距离A更近，则将顶点A的当前范围设置为当前范围的右半部分，并转到步骤3；否则将顶点A的当前范围设置为当前范围的左半部分，并转到步骤3。

复杂度：排序O(n*log n)，搜索O(n*log n)（二分和线性搜索的组合）。

- Evgeny Kluev

Answer 3

我认为有一种线性时间算法。请参考 Steiger 和 Streinu 的论文“洪灯照明”。他们的算法适用于任何 k1、k2、k3，使它们的总和为 n。因此，k1=k2=k3=n/3 是一个特殊情况。

以下是您可以找到该文章的链接。http://www.sciencedirect.com/science/article/pii/S0925772197000278 CiteSeerX 链接为 http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.53.4634

- Debajyoti Mondal

---

欢迎来到Stack Overflow。这个答案并没有太多帮助，您能否详细阐述一下这篇文章为什么对这个问题很重要？是否可以引用这篇文章？能否提供文章摘要或全文的链接？ - vidstige

谢谢vidstige，我已经添加了链接。 - Debajyoti Mondal

Answer 4

这里有一种方法，需要 O(log n) 次成本为 n 的遍历。

每次遍历都从一个初始点开始，将三角形分成三个子三角形。如果每个子三角形都有 n 个点，我们就完成了。如果没有，考虑到离所需的 n 最远的子三角形。暂且假设它有太多点。不平衡总和为零，因此另外两个子三角形中至少有一个点太少。第三个子三角形要么也太少，要么正好有 n 个点 - 否则原始子三角形不会有最大的差异。

取最不平衡的子三角形并考虑沿着离开它的直线移动中心点。随着您这样做，最不平衡点的不平衡度将减少。对于三角形中的每个点，在移动中心点时，您可以计算出该点何时穿过或离开最不平衡的子三角形。因此，您可以在时间 n 内计算出将中心点移动到哪里以使最不平衡的三角形具有任何所需数量。

随着您移动中心点，您可以选择点是在还是离最不平衡的子三角形之内，但您无法选择它们去哪个或来自哪个其他两个子三角形 - 但是您可以轻松预测从您沿着的线的哪一侧滑动中心点它们所在的位置，因此您可以沿着这条线移动中心点，在移动后获得最低最大偏差。在最坏的情况下，所有移动的点都进入或退出完全平衡的子三角形。但是，如果不平衡的子三角形有n + k个点，则通过移动其中的k/2个点，您最多可以将其移动到与先前平衡的子三角形相比差k/2的情况。第三个子三角形仍然可能向另一个方向不平衡k个点，但在这种情况下，第二次遍历将将最大不平衡度降至小于k/2。

因此，在不平衡度较大的情况下，我们可以通过上述算法的两次遍历以最劣情况为界限将其缩小一个常数因子，因此在O(log n) 遍历后，不平衡度将足够小，以至于我们只需要担心多余不超过一个点的特殊情况。在这里，我猜测此类特殊情况的数量在程序中是可以枚举的，并且成本只需进行小常数加法。

- mcdowella