为了一个个人项目，我需要找出两条三次贝塞尔曲线是否相交。我不需要知道它们在哪里相交，我只需要知道它们是否相交。然而，我需要快速完成这项工作。
我在网上搜寻到很多资源，其中有一个问题的答案看起来很有希望，在这里可以找到。
因此，经过我了解了Sylvester矩阵、行列式、消元式以及为什么它有用，我认为我已经理解了解决方案的原理。但是，事实并非如此，它并不如此有效。
我在网上搜寻到很多资源，其中有一个问题的答案看起来很有希望，在这里可以找到。
因此，经过我了解了Sylvester矩阵、行列式、消元式以及为什么它有用，我认为我已经理解了解决方案的原理。但是，事实并非如此，它并不如此有效。
实验验证
我使用我的绘图计算器绘制了两个相交的贝塞尔样条曲线（我们称之为B 0和B 1）。它们的坐标如下（P 0，P 1，P 2，P 3）：(1, 1) (2, 4) (3, 4) (4, 3)
(3, 5) (3, 6) (0, 1) (3, 1)
结果如下，其中B0是“水平”曲线，B1是另一条曲线:
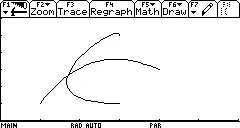
按照前面提到的问题的最佳答案的指示，我将B0减去了B1。这给了我两个方程式（X轴和Y轴），根据我的计算器，它们是:
x = 9t^3 - 9t^2 - 3t + 2
y = 9t^3 - 9t^2 - 6t + 4
西尔维斯特矩阵
然后我根据这个构建了以下的西尔维斯特矩阵：
9 -9 -3 2 0 0
0 9 -9 -3 2 0
0 0 9 -9 -3 2
9 -9 -6 4 0 0
0 9 -9 -6 4 0
0 0 9 -9 -6 4
之后，我编写了一个用于计算矩阵行列式的C++函数，使用的是Laplace展开法：
template<int size>
float determinant(float* matrix)
{
float total = 0;
float sign = 1;
float temporaryMatrix[(size - 1) * (size - 1)];
for (int i = 0; i < size; i++)
{
if (matrix[i] != 0)
{
for (int j = 1; j < size; j++)
{
float* targetOffset = temporaryMatrix + (j - 1) * (size - 1);
float* sourceOffset = matrix + j * size;
int firstCopySize = i * sizeof *matrix;
int secondCopySize = (size - i - 1) * sizeof *matrix;
memcpy(targetOffset, sourceOffset, firstCopySize);
memcpy(targetOffset + i, sourceOffset + i + 1, secondCopySize);
}
float subdeterminant = determinant<size - 1>(temporaryMatrix);
total += matrix[i] * subdeterminant * sign;
}
sign *= -1;
}
return total;
}
template<>
float determinant<1>(float* matrix)
{
return matrix[0];
}
对于相对较小的矩阵（2x2、3x3和4x4），似乎工作得相当不错，所以我期望它也可以适用于6x6的矩阵。但是我并没有进行广泛的测试，有可能它存在问题。
问题
如果我正确理解了另一个问题的答案，则由于曲线相交，行列式应该为0。然而，给我的程序提供上面我制作的Sylvester矩阵时，结果是-2916。
这是我出错还是他们出错？确定两个三次Bézier曲线是否相交的正确方法是什么？
(-P0 + 3*P1 - 3*P2 + P4) * t^3 + 3*(P0 - 2*P1 + P2) * t^2 - 3*(P0 - P1) * t + P0；而我展示的两个方程只是两条曲线的 X 和 Y 函数相减。WolframAlpha 证实它们是相同的。 - zneak