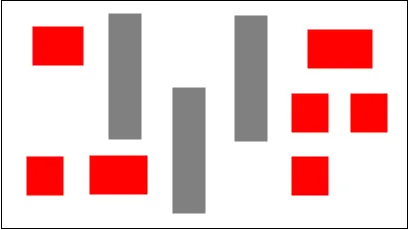
将矩形按照它们最左边的坐标从左到右排序,如下图所示:
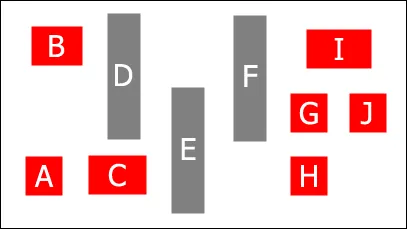
然后,从左到右迭代每个矩形,看看它们与哪些在它们左侧的矩形在垂直方向上重叠(即,如果将它们向左移动,它们会碰到哪些矩形)。
A 和 B 到达左边窗户而不会碰到任何其他矩形。
C 碰到了 A。
D 碰到了 B。
E 碰到了 A、C 和 D。
F 碰到了 B、D 和 E。
G 碰到了 D、E 和 F。
H 碰到了 A、C 和 E。
I 碰到了 B、D 和 F。
J 碰到了 D、E、F 和 G。
使用这些信息构建如下所示的图形。当一个矩形碰撞到多个其他矩形时,例如 E 碰到了 A、C 和 D,并且这些矩形本身属于同一个分支,例如 A 和 C,则只将其连接到最右侧的矩形,即矩形 C。
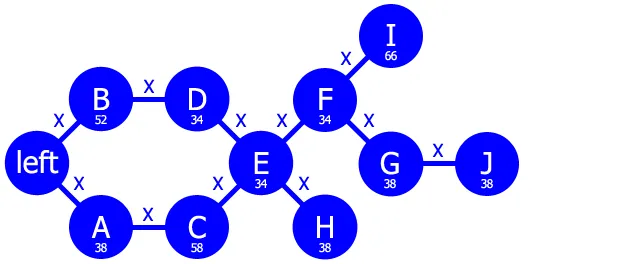
然后,将每个矩形的宽度以像素为单位存储在图表中。然后我们将尝试找到边的权重X,它表示矩形之间空白的宽度。
为此,我们需要在图表中找到多条路径。首先,我们搜索最长的路径,即不考虑它们的宽度的路径,例如:
左窗口边缘 → A → C → E → F → G → J
左窗口边缘 → B → D → E → F → G → J
然后,我们检查哪一条路径具有最大的组合宽度:
左窗口边缘 → A → C → E → F → G → J = 240
然后,我们查看较短的路径,看看它们是否具有更大的宽度:
左窗口边缘 → A → C → E → F → I = 230
左窗口边缘 → B → D → E → F → I = 220
左窗口边缘 → A → C → E → H = 168
左窗口边缘 → B → D → E → H = 158
在这个例子中,没有任何一条更短的路径具有更大的宽度。如果有一些路径具有更大的宽度,我们也必须考虑每个长度的最宽路径。现在,我们只需要看这条路径:
左窗口边缘 → A → C → E → F → G → J = 240
将这条路径连接到右窗口边缘,使其多出一条边;现在有7条宽度为X的边。矩形的总宽度为240像素,因此,如果窗口宽度为450像素,则X = (450-240) / 7 = 30像素。如果有几条路径需要考虑,您将选择X的最小值。
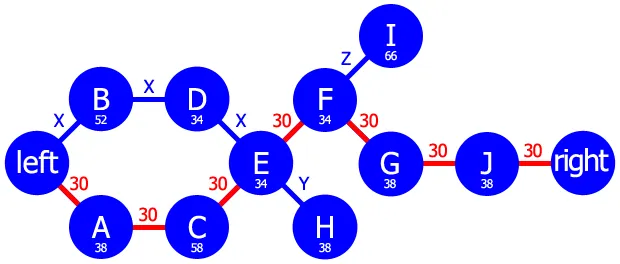
路径中具有最小结果的矩形将恰好在它们之间有X像素的空间;其他矩形则有一些余地。您可以将X输入为图中最长路径中边的权重,然后使用图来进一步计算其他矩形的等距离间距。或者,您可以将它们与它们的左侧或右侧邻居相距X。
对于更复杂的情况,假设在示例中矩形I宽90像素,矩形H宽120像素。这些将是路径:
6个矩形:
左窗口边缘 → A → C → E → F → G → J = 240
左窗口边缘 → B → D → E → F → G → J = 230
5个矩形:
左窗口边缘 → A → C → E → F → I = 254
左窗口边缘 → B → D → E → F → I = 244
4个矩形:
左窗口边缘 → A → C → E → H = 250
左窗口边缘 → B → D → E → H = 240
然后要考虑的路径是:
左窗口边缘 → A → C → E → F → G → J = 240
因为它是拥有最多(6)矩形的最宽路径,以及:
左窗口边缘 → A → C → E → F → I = 254
因为它是拥有5个矩形的最宽路径,并且比6个矩形的路径更宽。
最宽的4个矩形路径比6个矩形路径更宽,但不比5个矩形路径更宽,因此可以忽略它。
这给出了以下条件:
240 + 7×X = W
254 + 6×X = W
因此,对于窗口宽度为290,结果如下:
240 + 7×X = 290 → X = 7
254 + 6×X = 290 → X = 6
因此,路径A→C→E→F→I确定了间距的宽度为6像素。
但是对于窗口宽度为390,结果如下:
240 + 7×X = 390 → X = 21
254 + 6×X = 390 → X = 22
因此,现在路径A→C→E→F→G→J确定了间距的宽度为21像素。