让斐波那契数列更快

Question

我需要编写一个简单的 Fibonacci 算法实现，并且优化它的速度。

这是我的初始实现：

public class Fibonacci {

    public static long getFibonacciOf(long n) {
        if (n== 0) {
            return 0;
        } else if (n == 1) {
            return 1;
        } else {
            return getFibonacciOf(n-2) + getFibonacciOf(n-1);
        }
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner (System.in);
        while (true) {
            System.out.println("Enter n :");
            long n = scanner.nextLong();
            if (n >= 0) {
                long beginTime = System.currentTimeMillis();
                long fibo = getFibonacciOf(n);
                long endTime = System.currentTimeMillis();

                long delta = endTime - beginTime;

                System.out.println("F(" + n + ") = " + fibo + " ... computed     in " + delta + " milliseconds");
            } else {
                break;

            }
        }

    }

}

如您所见，我正在使用System.currentTimeMillis()来获得计算斐波那契数列所需时间的简单测量。

随着你在下面这张图片中看到的，这个实现变得越来越慢

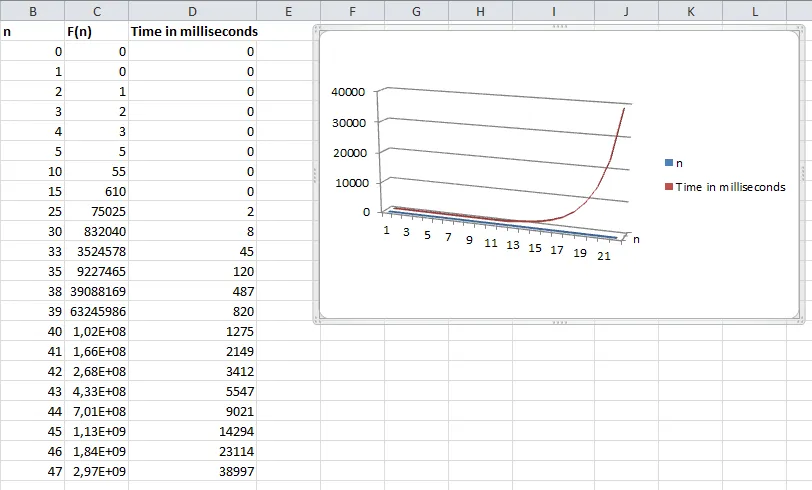
因此，我有一个简单的优化想法。将前面的值放入HashMap中，并且不再每次重新计算它们，而是直接从HashMap中获取它们（如果存在）。如果它们不存在，则将它们放入HashMap中。

以下是新版本的代码：

public class FasterFibonacci {

    private static Map<Long, Long> previousValuesHolder;
    static {
        previousValuesHolder = new HashMap<Long, Long>();
        previousValuesHolder.put(Long.valueOf(0), Long.valueOf(0));
        previousValuesHolder.put(Long.valueOf(1), Long.valueOf(1));
    }
    public static long getFibonacciOf(long n) {
        if (n== 0) {

            return 0;
        } else if (n == 1) {
            return 1;
        } else {
            if (previousValuesHolder.containsKey(Long.valueOf(n))) {
                return previousValuesHolder.get(n);
            } {

                long newValue = getFibonacciOf(n-2) + getFibonacciOf(n-1);
                previousValuesHolder.put(Long.valueOf(n),     Long.valueOf(newValue));
                return newValue;
            }

        }
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner (System.in);
        while (true) {
            System.out.println("Enter n :");
            long n = scanner.nextLong();
            if (n >= 0) {
                long beginTime = System.currentTimeMillis();
                long fibo = getFibonacciOf(n);
                long endTime = System.currentTimeMillis();

                long delta = endTime - beginTime;

                System.out.println("F(" + n + ") = " + fibo + " ... computed     in " + delta + " milliseconds");
            } else {
                break;

            }
        }

    }

这个改变使得计算非常快。它在很短的时间内计算出从2到103的所有值，而且在F(104)（给我F(104)=-7076989329685730859，这是错误的）处发生了long溢出。我觉得它如此之快以至于**我想知道我的代码是否有任何错误（感谢您的检查并让我知道）**。请看第二张图片：

我的更快的斐波那契算法实现是否正确（对我来说似乎是因为它获得与第一个版本相同的值，但由于第一个版本太慢了，我无法使用它计算更大的值，如F(75)）？我还可以用什么其他方法使它更快？或者有没有更好的方式使它更快？另外，如何计算更大的斐波那契数列（例如150、200）而不会发生long溢出？虽然它看起来很快，但我想把它推到极限。我记得Abrash先生曾经说过：“最好的优化器在你的两个耳朵之间”，所以我相信它仍然可以改进。谢谢你的帮助。

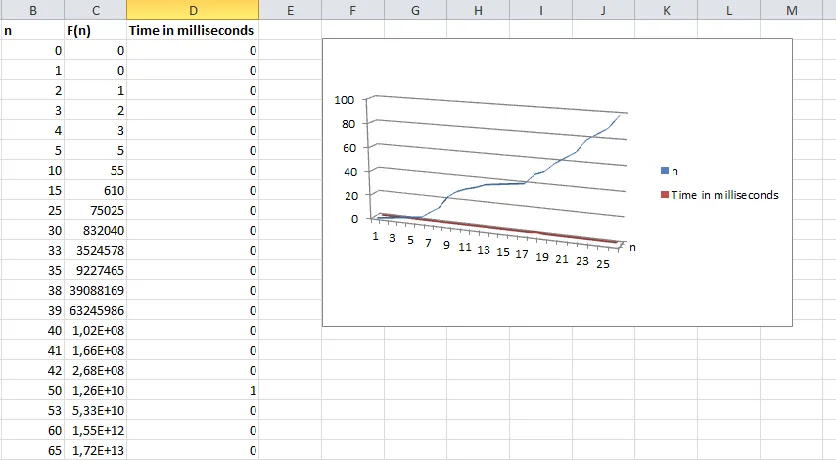
[编辑说明:]尽管这个问题解决了我的问题，但是从上面可以看出我还有其他问题。

- alainlompo

---

您遇到的问题不是栈溢出，而是长整型溢出，因为结果超过了长整型变量的最大值。您可以使用 BigInteger 类型来代替长整型。 - Eran

请尝试编写该算法的迭代版本。 - fvannee

我会给你一些提示。首先，如@fvannee所建议的那样，实现迭代版本；其次，专注于计算F(n)所需的最小要素。你了解DP吗？ - Pranalee

你可以使用矩阵（只有2x2，不用担心）的乘方（通过平方），但这只对非常大的数字有帮助，比如F(500+)。 - harold

为了解决长整型溢出问题，使用BigInteger代替长整型作为斐波那契数列的数据类型。 - MinecraftShamrock

Answer 1

动态规划

思路：不必重复计算相同的值，只需将已经计算过的值保存起来，在需要时直接调用即可。

f(n)=f(n-1)+f(n-2)，其中f(0)=0，f(1)=1。 当你已经计算出f(n-1)时，如果你保存了f(n)和f(n-1)的值，那么你可以轻松地计算出f(n)。

首先，让我们使用Bignums数组 A[1..200]，并将它们初始化为-1。

伪代码

fact(n)
{
if(A[n]!=-1) return A[n];
A[0]=0;
A[1]=1;
for i=2 to n
  A[i]= addition of A[i],A[i-1];
return A[n]
}

这个算法的时间复杂度为O(n)，你可以自己试一下。

这种技术也称为记忆化搜索。

思路

动态规划（通常简称 DP）是一种解决特定问题类的非常强大的技术。它需要非常优雅的方法和简单的思维，编码部分也很容易。其思想非常简单：如果您已经解决了给定输入的问题，则保存结果以供将来参考，以避免再次解决相同的问题……简而言之，就是“记住您的过去”。

如果给定的问题可以被分解成更小的子问题，并且这些更小的子问题又分解成更小的子问题，在这个过程中，如果您观察到某些重叠的子问题，那么它就是 DP 的一个大提示。此外，子问题的最优解对给定问题的最优解有贡献（称为 最优子结构性质）。

有两种方法可以实现。

  

1.) 自顶向下：通过拆分给定的问题开始解决它。如果您看到问题已经解决了，只需返回保存的答案即可。如果没有解决，解决它并保存答案。这通常很容易想到，并且非常直观。这称为记忆化搜索（我使用了这个方法）。

     

2.) 自底向上：分析问题并查看解决子问题的顺序，从微不足道的子问题开始，逐步解决给定问题。在此过程中，保证在解决问题之前解决了子问题。这称为动态规划。（MinecraftShamrock运用了这个思路）

---

更多内容！

我们追求更好的解决方案的探索并没有结束。您将看到一种不同的思路-

  

如果您知道如何解决 递归关系，然后就可以找到此关系的解决方案

f(n)=f(n-1)+f(n-2) ，其中 f(0)=0，f(1)=1

解决它后，您将得到该公式-

f(n)= (1/sqrt(5))((1+sqrt(5))/2)^n - (1/sqrt(5))((1-sqrt(5))/2)^n

可写成更紧凑的形式

f(n)=floor((((1+sqrt(5))/2)^n) /sqrt(5) + 1/2)

复杂度

您可以在 O(logn) 次操作中计算一个数的幂。 您必须学习 幂运算。

编辑：需要指出的是，这并不意味着斐波那契数可以在 O(logn) 的时间内找到。实际上，我们需要计算的位数是线性增长的。可能是因为我说的位置有误，似乎宣称可以在 O(logn) 的时间内计算一个数的阶乘。 [Bakurui，MinecraftShamrock对此进行了评论]

- user2736738

---

@Pranalee：抱歉！我以为如果他不知道，我至少应该给他一个想法。 - user2736738

@Mikhail：是的！渐进地它们是相同的。但我认为使用简单数组会给出更好的运行时间。如果您发现任何错误，请告知我，我将学习并更改我的帖子。 - user2736738

@alainlompo 不用担心.. :) 我只是想让你在查看解决方案之前先尝试一些迭代/动态规划。 - Pranalee

你在谈论矩阵求幂。这也是log(n)的复杂度。但是在两种情况下，都需要了解特征方程的概念。这就是为什么我提到它的原因。 - user2736738

传播第n个数字可以在logn时间内计算的虚假信息是-1。这是错误的。斐波那契数呈指数增长，因此必须计算O(n)位，这需要O(n)复杂度。使用O(logn)乘法的事实并不改变它们需要O(n)时间的事实。如果您认为乘法是O(1)，则您要么使用了错误的计算模型，要么使用了有界数字。在后一种情况下，您可以在O(1)时间内计算斐波那契数（因为它们是有界的...） - Bakuriu

Answer 2

如果您需要频繁计算第n个斐波那契数，我建议使用Amalsom的答案。

但是，如果您想计算非常大的斐波那契数，您将会耗尽内存，因为您在存储所有较小的斐波那契数。以下伪代码仅保留最后两个斐波那契数，即它需要更少的内存：

fibonacci(n) {
    if n = 0: return 0;
    if n = 1: return 1;
    a = 0;
    b = 1;
    for i from 2 to n: {
        sum = a + b;
        a = b;
        b = sum;
    }
    return b;
}

分析
这个算法可以用很少的内存计算出非常大的斐波那契数：我们有O(n)时间复杂度，因为循环重复n-1次。空间复杂度也很有趣：第n个斐波那契数的长度为O(n)，这很容易证明：
F_n <= 2 * F_n-1
这意味着第n个斐波那契数最多只比其前一个数大两倍。在二进制中将一个数翻倍相当于向左移动一位，这增加了必要位数的数量。因此，表示第n个斐波那契数最多需要O(n)的空间。我们最多在内存中存储三个连续的斐波那契数，因此总空间消耗为O(n) + O(n-1) + O(n-2) = O(n)。相比之下，记忆化算法始终将前n个斐波那契数保留在内存中，这使得空间消耗为O(n) + O(n-1) + O(n-2) + ... + O(1) = O(n^2)。

那么应该选择哪种方式呢？
只有当需要非常频繁地使用斐波那契数时，才有必要将所有较低的斐波那契数保留在内存中。这是时间和内存消耗之间平衡的问题。

- MinecraftShamrock

---

有一个闭合形式，可以用来计算大的斐波那契数，时间复杂度为O(1)。 - Boris the Spider

这是一个非常明智的方法 - 它避免了递归灾难，如果你被要求使用铅笔和纸找到Fib（100）（并且你不能记住具有黄金分割的闭合形式），那么你可能会这样做。 - Floris

@BoristheSpider 这与构建一个固定的查找表并查找最大斐波那契数的方式相同。实际上，查找表将是最快的解决方案。问题在于：它们仅适用于有界数字。如果您删除有界假设，则复杂度必须为O(n)。 - Bakuriu

@MinecraftShamrock，我使用BigInteger实现了你分享的代码。它非常快速，可以计算非常大的数字。在2毫秒内计算出F(2000)...谢谢！ - alainlompo

Answer 3

避免使用斐波那契递归，而是使用身份验证

(F(2n), F(2n-1)) = (F(n)^2 + 2 F(n) F(n-1), F(n)^2+F(n-1)^2)
(F(2n+1), F(2n)) = (F(n+1)^2+F(n)^2, 2 F(n+1) F(n) - F(n)^2)

这允许你通过(F(k+1), F(k))计算出(F(m+1), F(m)), 其中k为m的一半。通过迭代和位移运算来实现除以2，这样就可以完全使用整数算术，在理论上实现以O(log n)速度进行平方指数运算。（好吧，是O(log n)次算术操作。因为你将处理具有大约n位数字的数字，所以一旦被迫切换到大数库，时间就不再是O(log n)了。在F(50)之后，您将溢出整数数据类型，该类型仅支持达到2^(31)）。

（很抱歉我记不清Java语言，无法在Java中实现此代码；任何想要实现的人都可以进行编辑）

- David E Speyer

---

这似乎是唯一一个时间复杂度为*O(log n)*的答案。 - abligh

请在您的答案中添加上述公式的推导。 - WestCoastProjects

以下网站对这种方法进行了很好的讨论和推导。http://www.nayuki.io/page/fast-fibonacci-algorithms - cspirou

@abligh 不是这样的。斐波那契数列需要O（n）时间，因为第n个斐波那契数有O（n）位。如果只考虑有限的数字，那么你可以轻松地实现O(1)时间，对于无限制的数字，你可以使用logn 乘法来计算第n个斐波那契数，但是它们不需要O(1)的时间！总时间仍然是O(n)。 - Bakuriu

我已经使用这些恒等式添加了一个答案。 - abligh

Answer 4

• Fibonacci(0) = 0
• Fibonacci(1) = 1
• 当 n >= 2 时，Fibonacci(n) = Fibonacci(n - 1) + Fibonacci(n - 2)

通常有两种方法来计算斐波那契数列：

1. Recursion:

   public long getFibonacci(long n) {
     if(n <= 1) {
       return n;
     } else {
       return getFibonacci(n - 1) + getFibonacci(n - 2);
     }
   }
   

   This way is intuitive and easy to understand, while because it does not reuse calculated Fibonacci number, the time complexity is about O(2^n), but it does not store calculated result, so it saves space a lot, actually the space complexity is O(1).

2. Dynamic Programming:

   public long getFibonacci(long n) {
     long[] f = new long[(int)(n + 1)];
     f[0] = 0;
     f[1] = 1;
     for(int i=2;i<=n;i++) {
       f[i] = f[i - 1] + f[i - 2];
     }
     return f[(int)n];
   }
   

   This Memoization way calculated Fibonacci numbers and reuse them when calculate next one. The time complexity is pretty good, which is O(n), while space complexity is O(n). Let's investigate whether the space complexity can be optimized... Since f(i) only requires f(i - 1) and f(i - 2), there is not necessary to store all calculated Fibonacci numbers.

   The more efficient implementation is:

   public long getFibonacci(long n) {
     if(n <= 1) {
       return n;
     }
     long x = 0, y = 1;
     long ans;
     for(int i=2;i<=n;i++) {
       ans = x + y;
       x = y;
       y = ans;
     }
     return ans;
   }
   

   With time complexity O(n), and space complexity O(1).

新增: 由于斐波那契数列增长非常迅速，long 只能处理不到 100 个斐波那契数。在 Java 中，我们可以使用 BigInteger 存储更多的斐波那契数。

- coderz

---

如果有错误的强烈陈述和非传统使用 "memorize" 而非 memoize，请注意阅读（并理解）其他答案，尤其是 David E Speyer 的答案。 - greybeard

@老前辈 感谢您的提醒，这里应该使用记忆化。回答已经修改。 - coderz

@coderz，“最高效的实现方式应该是”采用迭代方法。请遵循@greybeard的建议。 - catch23

@nazar_art 已更新，DP 不是最高效的方式，我删除了“最高效”的词。最高效的方式应该是 O(logn)。 - coderz

@coderz 斐波那契数列需要 O(n) 的时间。如果您使用有界整数，则所有这些算法都是 O(1)（最快的方法是：创建一个表并查找）。对于无界整数，您可以使用 log n 个乘法来计算它，这些乘法不是 O(1)，它们仍然需要总共 O(n) 的时间。 - Bakuriu

@Bakuriu 是的，计算f(n)的时间复杂度可以是O(logn)。而如果使用预先计算从f(1)到f(n)，则需要n*logn的时间复杂度。但是一旦计算并保存在内存中，查询f(k)，其中1<=k<=n，只需要O(1)的时间复杂度。 - coderz

Answer 5

预先计算大量的fib(n)结果，并将它们作为查找表存储在算法内部。这样，就能够获得免费的“速度”。

现在如果你需要计算fib(101)，并且你已经存储了0到100的斐波那契数列，那么这就像尝试计算fib(1)一样简单。

很有可能这不是作业要求的内容，但这是一个完全合法的策略，基本上就是缓存思想从算法中进一步提取。如果你知道你经常需要计算前100个斐波那契数列，并且需要非常快地完成它，那么没有比O（1）更快的方法了。因此，完全超出带宽计算这些值，并将它们存储起来以便以后查找。

当然，在计算它们的同时也要进行缓存：重复的计算是浪费。

- MushinNoShin

---

这并没有真正加快任何东西，你必须在任何基准测试中包括初始化时间。 - Boris the Spider

你假设初始化需要作为基准测试的一部分进行。如果我们只需要一个快速返回fib(n)的函数，并且不介意它占用大量空间，我们可以预先计算并以某种方式将其与代码打包在一起（可以硬编码为开关或混合到某种键值存储中）。这是一种优雅的算法优化吗？不！这是针对特定用例的完全“hack”。我听到的只有快速，而O(1)就是最快的。当然，如果我是专业人士，我会提出存储空间方面的问题。 - MushinNoShin

抱歉，但是“我会预先计算并将其保存到文件中”不是一个有效的算法优化。 - Boris the Spider

在算法优化方面，可能并不适用。但在实际应用中，您肯定希望硬编码这些值。特别是如果您使用的是32位或64位整数（而不是任意精度整数），那么这一点尤为重要： F_48大于2^32，F_94大于2^64，因此甚至无法返回更大的值。对于生产用途，简单的 return FIBS [n] if n <MAX_FIB else OverflowError() 会是最优选择。 - wchargin

Answer 6

这里有一段代码，采用迭代方式而非递归。

输出示例：

Enter n: 5
F(5) = 5 ... computed in 1 milliseconds
Enter n: 50
F(50) = 12586269025 ... computed in 0 milliseconds
Enter n: 500
F(500) = ...4125 ... computed in 2 milliseconds
Enter n: 500
F(500) = ...4125 ... computed in 0 milliseconds
Enter n: 500000
F(500000) = 2955561408 ... computed in 4,476 ms
Enter n: 500000
F(500000) = 2955561408 ... computed in 0 ms
Enter n: 1000000
F(1000000) = 1953282128 ... computed in 15,853 ms
Enter n: 1000000
F(1000000) = 1953282128 ... computed in 0 ms

为了更好的视觉效果，一些结果被省略并用...表示。

代码片段:

public class CachedFibonacci {
    private static Map<BigDecimal, BigDecimal> previousValuesHolder;
    static {
        previousValuesHolder = new HashMap<>();
        previousValuesHolder.put(BigDecimal.ZERO, BigDecimal.ZERO);
        previousValuesHolder.put(BigDecimal.ONE, BigDecimal.ONE);
    }

    public static BigDecimal getFibonacciOf(long number) {
        if (0 == number) {
            return BigDecimal.ZERO;
        } else if (1 == number) {
            return BigDecimal.ONE;
        } else {
            if (previousValuesHolder.containsKey(BigDecimal.valueOf(number))) {
                return previousValuesHolder.get(BigDecimal.valueOf(number));
            } else {
                BigDecimal olderValue = BigDecimal.ONE,
                        oldValue = BigDecimal.ONE,
                        newValue = BigDecimal.ONE;

                for (int i = 3; i <= number; i++) {
                    newValue = oldValue.add(olderValue);
                    olderValue = oldValue;
                    oldValue = newValue;
                }
                previousValuesHolder.put(BigDecimal.valueOf(number), newValue);
                return newValue;
            }
        }
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        while (true) {
            System.out.print("Enter n: ");
            long inputNumber = scanner.nextLong();
            if (inputNumber >= 0) {
                long beginTime = System.currentTimeMillis();
                BigDecimal fibo = getFibonacciOf(inputNumber);
                long endTime = System.currentTimeMillis();
                long delta = endTime - beginTime;

                System.out.printf("F(%d) = %.0f ... computed in %,d milliseconds\n", inputNumber, fibo, delta);
            } else {
                System.err.println("You must enter number > 0");
                System.out.println("try, enter number again, please:");
                break;
            }
        }
    }
}

这种方法比递归版本要快得多。

在这种情况下，迭代解决方案往往会更快一些，因为每个递归方法调用都需要一定的处理器时间。原则上，如果递归方法遵循简单模式，则智能编译器可以避免递归方法调用，但大多数编译器并不会这样做。从这个角度来看，迭代解决方案更可取。

更新：

Java 8发布后，Stream API可用，还有一种计算斐波那契数列的方法。

使用JDK 17.0.2进行验证。

代码：

public static BigInteger streamFibonacci(long n) {
    return Stream.iterate(new BigInteger[]{BigInteger.ONE, BigInteger.ONE},
                    p -> new BigInteger[]{p[1], p[0].add(p[1])})
            .limit(n)
            .reduce((a, b) -> b)
            .get()[0];
}

测试输出：

Enter n (q for quit): 5
F(5) = 5 ... computed in 2 ms
Enter n (q for quit): 50
F(50) = 1258626902 ... computed in 0 ms
Enter n (q for quit): 500
F(500) = 1394232245 ... computed in 3 ms
Enter n (q for quit): 500000
F(500000) = 2955561408 ... computed in 4,343 ms
Enter n (q for quit): 1000000
F(1000000) = 1953282128 ... computed in 19,280 ms

结果非常不错。
请记住，...只会截断实数后面的所有数字。

- catch23

---

这个 new BigInteger(String.valueOf(0)) 究竟是什么？使用 BigDecimal.ZERO 有什么问题吗？ - Boris the Spider

@BoristheSpider 我纠正了这些笨拙的地方。谢谢。 - catch23

Answer 7

这里有一种经过验证的方法可以在 O(log n) 的时间复杂度内完成（由于循环运行 log n 次）:

/* 
 * Fast doubling method
 * F(2n) = F(n) * (2*F(n+1) - F(n)).
 * F(2n+1) = F(n+1)^2 + F(n)^2.
 * Adapted from:
 *    https://www.nayuki.io/page/fast-fibonacci-algorithms
 */
private static long getFibonacci(int n) {
    long a = 0;
    long b = 1;
    for (int i = 31 - Integer.numberOfLeadingZeros(n); i >= 0; i--) {
        long d = a * ((b<<1) - a);
        long e = (a*a) + (b*b);
        a = d;
        b = e;
        if (((n >>> i) & 1) != 0) {
            long c = a+b;
            a = b;
            b = c;
        }
    }
    return a;
}

我假设（这是常规做法）无论位数如何，一次乘/加/任何操作都是恒定时间的，即将使用固定长度的数据类型。 此页面介绍了几种方法，其中这是最快的。我只是为了可读性而将其从使用BigInteger转换过来。以下是BigInteger版本：

/* 
 * Fast doubling method.
 * F(2n) = F(n) * (2*F(n+1) - F(n)).
 * F(2n+1) = F(n+1)^2 + F(n)^2.
 * Adapted from:
 *    http://www.nayuki.io/page/fast-fibonacci-algorithms
 */
private static BigInteger getFibonacci(int n) {
    BigInteger a = BigInteger.ZERO;
    BigInteger b = BigInteger.ONE;
    for (int i = 31 - Integer.numberOfLeadingZeros(n); i >= 0; i--) {
        BigInteger d = a.multiply(b.shiftLeft(1).subtract(a));
        BigInteger e = a.multiply(a).add(b.multiply(b));
        a = d;
        b = e;
        if (((n >>> i) & 1) != 0) {
            BigInteger c = a.add(b);
            a = b;
            b = c;
        }
    }
    return a;
}

- abligh

---

谢谢。我会测试它并与这里分享的其他方法进行比较。请注意，使用长版本的Fibonacci时，在F(104)处会出现长时间溢出。 F(104)的值为-7076989329685730859。因此，我也会尝试BigInteger版本。 - alainlompo

@alainlompo 我已经添加了 BigInteger 版本以保证完整性。 - abligh

太棒了！！！谢谢。我会使用它。 - alainlompo

值得注意的是，numberOfLeadingZeros 在实践中被 JIT 编译为单个 x86 指令。 - wchargin

@user2812818，你的（正确的）修复在我处理之前被拒绝了。multiply(x,y)是由一个辅助函数提供的，我没有像参考文献中那样放上去。 - abligh

Answer 8

之前我也采用了类似的方法，但我刚刚意识到还有另一种优化方法。

如果你知道两个相邻的大数，那么可以以此为起点进行计算。例如，如果你知道F(100)和F(101)，那么计算F(104)的难度 (*) 大约与基于F(0)和F(1)计算F(4)相当。

从上往下迭代计算与使用缓存递归计算相比，在计算方面效率相同，但使用的内存较少。

经过一些计算，我还意识到，对于任何给定的z < n：

F(n)=F(z) * F(n-z) + F(z-1) * F(n-z-1)

如果n是奇数，并且你选择z=(n+1)/2，那么这就简化为

F(n)=F(z)^2+F(z-1)^2

我认为你应该能够通过我尚未找到的一种方法使用此公式，可以在以下操作次数内找到F(n)：

n的位数加倍次数（如上所述）+ n中1的位数的加法次数；在104的情况下，这将是（7个位，3个‘1’位）= 14个乘法（平方），10个加法。

（*）假设两个数字相加需要的时间相同，无论这两个数字的大小如何。

- AMADANON Inc.

---

z=2n？实际上应该是2z=n或z=n/2。你的序数分配可能与其他人不同：F（0）的值是多少？你对可用性的印象非常准确：再看一下David E Speyer的答案。 - greybeard

@老程序员 谢谢您的回复 :) 是的，您说得对；z=n/2，并且我从F(0)=1，F(1)=1开始；如果我能算出来，我会尝试修正我的数学问题。 - AMADANON Inc.