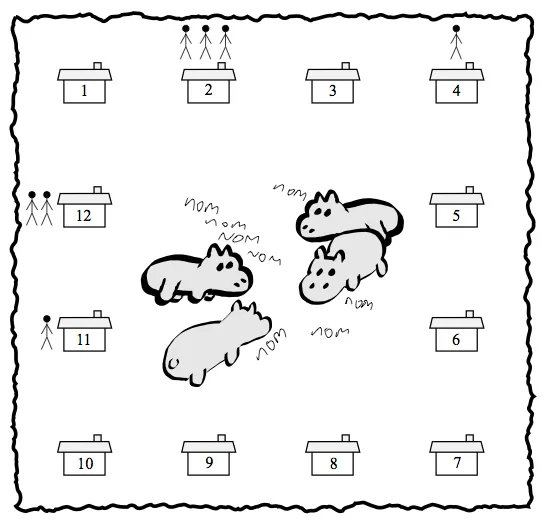
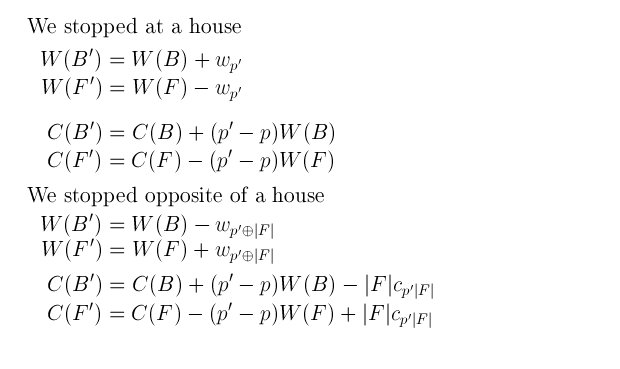这里是一个不太数学化的解决方案,可以在O(n)时间内运行。
让我们将房屋(从0开始索引)分为两个不相交的集合:
- F,“前面”,人们顺时针走到房子
- B,“后面”,人们逆时针走到房子
还有一个单独的房子p,标记着植物将被建造的当前位置。
我以给出的示例图为基础进行说明。
按照惯例,让我们将一半的房子分配给F,将恰好少一个房子分配给B。
- F包含6个房子
- B包含5个房子
使用简单的模数算术,我们可以轻松地通过
(p + offset) % 12 访问房屋,这要归功于 Python 对模运算符的合理实现,与
some other popular languages 相比非常不同。
如果我们随意选择
p 的位置,我们可以轻松地确定
O(L) 的水消耗量。
我们可以针对不同的
p位置再次执行此操作,以达到
O(L^2)的运行时间。
然而,如果我们只将
p向右移动一个位置,我们可以通过做出一些巧妙的观察来确定
O(1)中的新消费情况:居住在
F(或分别为
B)的人数决定了当我们设置
p' = p+1时,
F的消费变化量(以及一些修正因为
F本身会改变)。我已经尽力在这里描述它。

我们最终得到了总运行时间为
O(L)。
该算法的程序在本文末尾。
但是我们可以做得更好。只要在集合之间没有房屋发生变化,添加的
c 和
w 将为零。我们可以计算这些步骤的数量并一次性完成它们。
当房屋发生以下情况时,房屋会改变集合:
- 当
p 在一个房屋上
- 当
p 在房屋的对面
在下面的图表中,我已经可视化了算法现在更新
C 和
W 所需停止的位置。
突出显示导致算法停止的房屋。
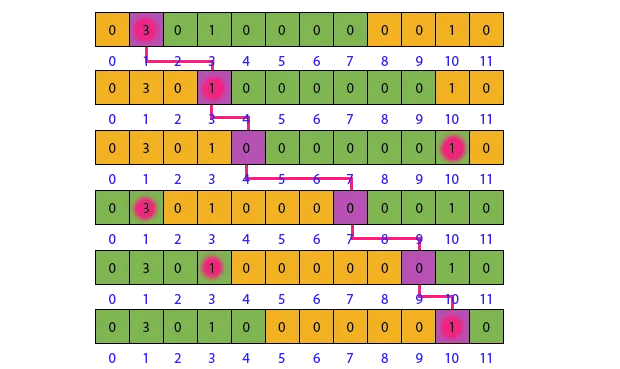
算法从一个房子开始(或者说是它的对面,稍后我们会看到原因),在这种情况下,恰好是一个房子。
同样,我们有消耗量
C(B) = 3*1 和
C(F) = 2 * 1。如果我们将
p 向右移动一位,那么就会给
C(B) 加上
4 并从
C(F) 中减去
1。如果我们再次将
p 向右移动一次,同样的事情会发生。
只要同样的两组房子分别向前和向后移动,
C 的变化就是恒定的。
现在我们稍微改变一下
B 的定义:它现在也包括
p!(这不会改变关于该算法优化版本的上述段落)。
这是因为当我们进入下一步时,我们将重复添加远离的房屋的权重。当
p 向右移动时,当前位置的房屋正在向远处移动,因此
W(B) 是正确的加数。
另一种情况是房子停止远离并再次靠近。在这种情况下,由于6*weight从一个C转移到另一个C,因此Cs会发生巨大变化。这是我们需要停止的另一种情况。
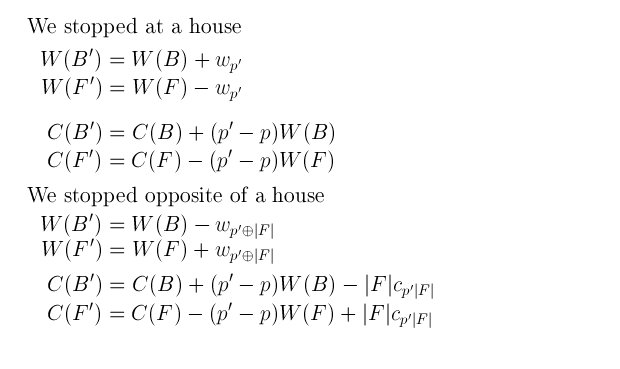
我希望你已经清楚了这个算法的工作原理和原因,所以我会在这里留下工作算法。如果有不清楚的地方,请询问。
O(n):
import itertools
def hippo_island(houses, L):
return PlantBuilder(houses, L).solution
class PlantBuilder:
def __init__(self, houses, L):
self.L = L
self.houses = sorted(houses)
self.changes = sorted(
[((pos + L /2) % L, -transfer) for pos, transfer in self.houses] +
self.houses)
self.starting_position = min(self.changes)[0]
def is_front(pos_population):
pos = pos_population[0]
pos += L if pos < self.starting_position else 0
return self.starting_position < pos <= self.starting_position + L // 2
front_houses = filter(is_front, self.houses)
back_houses = list(itertools.ifilterfalse(is_front, self.houses))
self.front_count = len(houses) // 2
self.back_count = len(houses) - self.front_count - 1
(self.back_weight, self.back_consumption) = self._initialize_back(back_houses)
(self.front_weight, self.front_consumption) = self._initialize_front(front_houses)
self.solution = (0, self.back_weight + self.front_weight)
self.run()
def distance(self, i, j):
return min((i - j) % self.L, self.L - (i - j) % self.L)
def run(self):
for (position, weight) in self.consumptions():
self.update_solution(position, weight)
def consumptions(self):
last_position = self.starting_position
for position, transfer in self.changes[1:]:
distance = position - last_position
self.front_consumption -= distance * self.front_weight
self.front_consumption += distance * self.back_weight
self.back_weight += transfer
self.front_weight -= transfer
if transfer < 0:
self.front_consumption -= self.L/2 * transfer
self.front_consumption += self.L/2 * transfer
last_position = position
yield (position, self.back_consumption + self.front_consumption)
def update_solution(self, position, weight):
(best_position, best_weight) = self.solution
if weight > best_weight:
self.solution = (position, weight)
def _initialize_front(self, front_houses):
weight = 0
consumption = 0
for position, population in front_houses:
distance = self.distance(self.starting_position, position)
consumption += distance * population
weight += population
return (weight, consumption)
def _initialize_back(self, back_houses):
weight = back_houses[0][1]
consumption = 0
for position, population in back_houses[1:]:
distance = self.distance(self.starting_position, position)
consumption += distance * population
weight += population
return (weight, consumption)
O(L)
def hippo_island(houses):
return PlantBuilder(houses).solution
class PlantBuilder:
def __init__(self, houses):
self.houses = houses
self.front_count = len(houses) // 2
self.back_count = len(houses) - self.front_count - 1
(self.back_weight, self.back_consumption) = self.initialize_back()
(self.front_weight, self.front_consumption) = self.initialize_front()
self.solution = (0, self.back_weight + self.front_weight)
self.run()
def run(self):
for (position, weight) in self.consumptions():
self.update_solution(position, weight)
def consumptions(self):
for position in range(1, len(self.houses)):
self.remove_current_position_from_front(position)
self.add_house_furthest_from_back_to_front(position)
self.remove_furthest_house_from_back(position)
self.add_house_at_last_position_to_back(position)
yield (position, self.back_consumption + self.front_consumption)
def add_house_at_last_position_to_back(self, position):
self.back_weight += self.houses[position - 1]
self.back_consumption += self.back_weight
def remove_furthest_house_from_back(self, position):
house_position = position - self.back_count - 1
distance = self.back_count
self.back_weight -= self.houses[house_position]
self.back_consumption -= distance * self.houses[house_position]
def add_house_furthest_from_back_to_front(self, position):
house_position = position - self.back_count - 1
distance = self.front_count
self.front_weight += self.houses[house_position]
self.front_consumption += distance * self.houses[house_position]
def remove_current_position_from_front(self, position):
self.front_consumption -= self.front_weight
self.front_weight -= self.houses[position]
def update_solution(self, position, weight):
(best_position, best_weight) = self.solution
if weight > best_weight:
self.solution = (position, weight)
def initialize_front(self):
weight = 0
consumption = 0
for distance in range(1, self.front_count + 1):
consumption += distance * self.houses[distance]
weight += self.houses[distance]
return (weight, consumption)
def initialize_back(self):
weight = 0
consumption = 0
for distance in range(1, self.back_count + 1):
consumption += distance * self.houses[-distance]
weight += self.houses[-distance]
return (weight, consumption)
结果:
>>> hippo_island([0, 3, 0, 1, 0, 0, 0, 0, 0, 0, 1, 2])
(7, 33)