这是浪费我早上时间的代码 [失效链接已移除]... 它不完整,但基本上可以工作。你可以从之前的链接 [失效] 获取笔记本或复制下面的代码。
请注意,不久前在ask.sagemath上出现了一个类似的问题。
与Sasha的解决方案几乎相同,使用符号矩阵定义
A = SymbolicMatrix["A", {n, k}]
对于一些字符串"A",它不必与符号A相同。好的,这是代码:
ClearAll[SymbolicMatrix]
Options[SymbolicMatrix] = {Transpose -> False, Conjugate -> False, MatrixPower -> 1}
输入方阵的简写形式(也可以适用于不同类型的矩阵...)
SymbolicMatrix[name_String, n:_Symbol|_Integer, opts : OptionsPattern[]] := SymbolicMatrix[name, {n, n}, opts]
转置、共轭、共轭转置和逆运算下的行为
SymbolicMatrix/:Transpose[SymbolicMatrix[name_String,{m_,n_},opts:OptionsPattern[]]]:=SymbolicMatrix[name,{n,m},
Transpose->!OptionValue[SymbolicMatrix,Transpose],Sequence@@FilterRules[{opts},Except[Transpose]]]
SymbolicMatrix/:Conjugate[SymbolicMatrix[name_String,{m_,n_},opts:OptionsPattern[]]]:=SymbolicMatrix[name,{m,n},
Conjugate->!OptionValue[SymbolicMatrix,Conjugate],Sequence@@FilterRules[{opts},Except[Conjugate]]]
SymbolicMatrix/:ConjugateTranspose[A:SymbolicMatrix[name_String,{m_,n_},opts:OptionsPattern[]]]:=Conjugate[Transpose[A]]
SymbolicMatrix/:Inverse[SymbolicMatrix[name_String,{n_,n_},opts:OptionsPattern[]]]:=SymbolicMatrix[name,{n,n},
MatrixPower->-OptionValue[SymbolicMatrix,MatrixPower],Sequence@@FilterRules[{opts},Except[MatrixPower]]]
SymbolicMatrix/:(Transpose|Conjugate|ConjugateTranspose|Inverse)[eye:SymbolicMatrix[IdentityMatrix,{n_,n_}]]:=eye
组合矩阵幂(包括单位矩阵)
SymbolicMatrix/:SymbolicMatrix[a_String,{n_,n_},opt1:OptionsPattern[]].SymbolicMatrix[a_,{n_,n_},opt2:OptionsPattern[]]:=SymbolicMatrix[a,{n,n},Sequence@@FilterRules[{opt1},Except[MatrixPower]],MatrixPower->Total[OptionValue[SymbolicMatrix,#,MatrixPower]&/@{{opt1},{opt2}}]]/;FilterRules[{opt1},Except[MatrixPower]]==FilterRules[{opt2},Except[MatrixPower]]
SymbolicMatrix[a_String,{n_,n_},opts:OptionsPattern[]]:=SymbolicMatrix[IdentityMatrix,{n,n}]/;OptionValue[SymbolicMatrix,{opts},MatrixPower]===0
SymbolicMatrix/:(A:SymbolicMatrix[a_String,{n_,m_},OptionsPattern[]]).SymbolicMatrix[IdentityMatrix,{m_,m_}]:=A
SymbolicMatrix/:SymbolicMatrix[IdentityMatrix,{n_,n_}].(A:SymbolicMatrix[a_String,{n_,m_},OptionsPattern[]]):=A
使用尺寸作为工具提示的漂亮打印。
Format[SymbolicMatrix[name_String,{m_,n_},opts:OptionsPattern[]]]:=With[{
base=If[OptionValue[SymbolicMatrix,MatrixPower]===1,
StyleBox[name,FontWeight->Bold,FontColor->Darker@Brown],
SuperscriptBox[StyleBox[name,FontWeight->Bold,FontColor->Darker@Brown],OptionValue[SymbolicMatrix,MatrixPower]]],
c=Which[
OptionValue[SymbolicMatrix,Transpose]&&OptionValue[SymbolicMatrix,Conjugate],"\[ConjugateTranspose]",
OptionValue[SymbolicMatrix,Transpose],"\[Transpose]",
OptionValue[SymbolicMatrix,Conjugate],"\[Conjugate]",
True,Null]},
Interpretation[Tooltip[DisplayForm@RowBox[{base,c}/.Null->Sequence[]],{m,n}],SymbolicMatrix[name,{m,n},opts]]]
Format[SymbolicMatrix[IdentityMatrix,{n_,n_}]]:=Interpretation[Tooltip[Style[\[ScriptCapitalI],Bold,Darker@Brown],n],SymbolicMatrix[IdentityMatrix,{n,n}]]
定义一些规则来处理 Dot。需要扩展它,使其能够处理标量等。同时,即使 A 或 B 不是方阵,如果 A.B 是方阵,则可以取 A.B 的逆。
SymbolicMatrix::dotdims = "The dimensions of `1` and `2` are not compatible";
Unprotect[Dot]; (*Clear[Dot];*)
Dot/:(a:SymbolicMatrix[_,{_,n_},___]).(b:SymbolicMatrix[_,{m_,_},___]):=(Message[SymbolicMatrix::dotdims,HoldForm[a],HoldForm[b]];Hold[a.b])/;Not[m===n]
Dot/:Conjugate[d:Dot[A_SymbolicMatrix,B__SymbolicMatrix]]:=Map[Conjugate,d]
Dot/:(t:Transpose|ConjugateTranspose)[d:Dot[A_SymbolicMatrix,B__SymbolicMatrix]]:=Dot@@Map[t,Reverse[List@@d]]
Dot/:Inverse[HoldPattern[d:Dot[SymbolicMatrix[_,{n_,n_},___]...]]]:=Reverse@Map[Inverse,d]
A_ .(B_+C__):=A.B+A.Plus[C]
(B_+C__).A_:=B.A+Plus[C].A
Protect[Dot];
使转置、共轭和共轭转置在加法运算中具有分配律。
Unprotect[Transpose, Conjugate, ConjugateTranspose];
Clear[Transpose, Conjugate, ConjugateTranspose];
Do[With[{c = c}, c[p : Plus[a_, b__]] := c /@ p], {c, {Transpose, Conjugate, ConjugateTranspose}}]
Protect[Transpose, Conjugate, ConjugateTranspose];
这里有一些简单的测试/示例
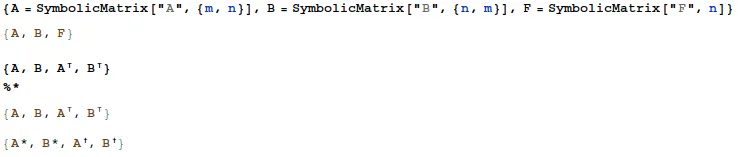

现在讨论处理组件扩展的代码。像Sasha的解决方案一样,我会重载Part函数。
Clear[SymbolicMatrixComponent]
Options[SymbolicMatrixComponent]={Conjugate->False,MatrixPower->1};
一些符号
Format[SymbolicMatrixComponent[A_String,{i_,j_},opts:OptionsPattern[]]]:=Interpretation[DisplayForm[SubsuperscriptBox[StyleBox[A,Darker@Brown],RowBox[{i,",",j}],
RowBox[{If[OptionValue[SymbolicMatrixComponent,{opts},MatrixPower]===1,Null,OptionValue[SymbolicMatrixComponent,{opts},MatrixPower]],If[OptionValue[SymbolicMatrixComponent,{opts},Conjugate],"*",Null]}/.Null->Sequence[]]]],
SymbolicMatrixComponent[A,{i,j},opts]]
代码提取矩阵的部分和矩阵的Dot乘积
需要添加检查以确保显式求和范围都是合理的。
SymbolicMatrix/:SymbolicMatrix[A_String,{m_,n_},opts:OptionsPattern[]][[i_,j_]]:=SymbolicMatrixComponent[A,If[OptionValue[SymbolicMatrix,{opts},Transpose],Reverse,Identity]@{i,j},Sequence@@FilterRules[{opts},Options[SymbolicMatrixComponent]]]
SymbolicMatrix/:SymbolicMatrix[IdentityMatrix,{m_,n_}][[i_,j_]]:=KroneckerDelta[i,j]
Unprotect[Part]; (*Clear[Part]*)
Part/:((c___.b:SymbolicMatrix[_,{o_,n_},OptionsPattern[]]).SymbolicMatrix[A_String,{n_,m_},opts:OptionsPattern[]])[[i_,j_]]:=With[{s=Unique["i",Temporary]},Sum[(c.b)[[i,s]]SymbolicMatrixComponent[A,If[OptionValue[SymbolicMatrix,{opts},Transpose],Reverse,Identity]@{s,j},Sequence @@ FilterRules[{opts}, Options[SymbolicMatrixComponent]]],{s,n}]]
Part/:(a_+b_)[[i_,j_]]:=a[[i,j]]+b[[i,j]]/;!And@@(FreeQ[#,SymbolicMatrix]&/@{a,b})
Part/:Hold[a_][[i_,j_]]:=Hold[a[[i,j]]]/;!FreeQ[a,SymbolicMatrix]
Protect[Part];
一些例子:

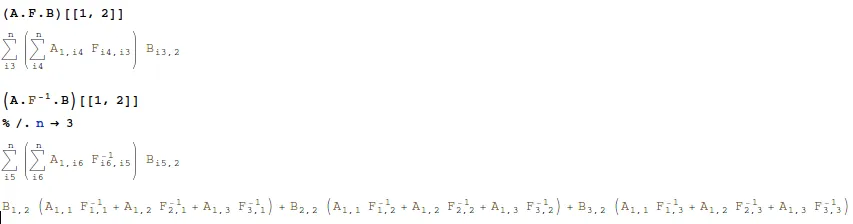


a_1b_1+...+a_nb_n可以方便地写成a_ib_i,其中隐含着对所有n的求和。点积、双重积、迹等都可以用这种方式简洁地表示。当涉及到指数时,事情会变得更混乱,因为符号会变得令人困惑(我不确定在这种情况下他们是否使用这种符号)。 - user616736